08级重庆名校高考文科数学4月测试试题

08级重庆名校高考文科数学4月测试试题

本试卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分。满分150分。考试时间120分钟。

第I卷（选择题 共50分）

一、选择题(本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.)

1．的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　 A．　　　　　　　　　　　　B． 　　　　　　　　　 C．　　　　　　　　　　D．

2．设集合，则下列关系中正确的是　　　　　　　　　（　　）

　 A．　　　　　　 B．　　　　　 C．　 　　　　　　D．

3．不等式组的解集为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　 A．　　　　　　　　B．　　　　　　　C．　　　　　　　D．（2，4）

4．在棱长为1的正方体AC₁中，对角线AC₁在六个面上的射影长度之和是　　　　　　 （　　）

　 A．6　 　　　　　　　　　　 B．　 　　　　　　　C．　　　　　　　　 D．

5．设向量与的模分别为6和5，夹角为120°，则等于　　　　　　　　　　　　　　 （　　）

　 A．　　　　　　　　　　　　B．　　　　　　　　　　C．　　　　　　　　　 D．

6．若的展开式中的系数是80，则实数a的值为　　　　　　　　　　　　　　　　　　　（　　）

　 A．-2　　　　　　　　　　　　 B．　　　　　　　　　 C．　　　　　　　　　　 D．2

7．已知函数f(x)是定义在R上的奇函数，当x<0时，，那么的值为 　　　　　　　　　　　 （　　）

　 A．3　　　　　　　　　　　　　B．-3　　　　　　　　　　　C．2　 　　　　　　　　　 D．-2

8．等比数列{a_n}，a_n>0, a₁a₃+a₃a₅+2a₂a₄=36，则a₂+a₄等于　　　　　　　　　　　　　　　　　　（　　）

　 A．6　　　　　　　　　　　　　B．10　　　　　　　　　　　 C．20　 　　　　　　　　 D．15

9．过双曲线的右焦点作直线l交双曲线于A、B两点，若，则这样的直线存在的条数是　　　　　　　 　　　　　　　　　　　　　　　　（　　）

A．1条　　　　　　　　　　B．2条　　　　　　　　　　C．3条　　　　　　　　　　D．4条

1,3,5

10．某种电热水器的水箱盛满水是200升，加热到一定温度可浴用，浴用时，已知每分钟放水34升，在放水的同时注水，t分钟注水2t²升，当水箱内水量达到最小值时，放水自动停止. 现假定每人洗浴用水65升，则该热水器一次至多可供　 （　　）

A．3人洗澡　　　　　　 B．4人洗澡　　　　　　 C．5人洗澡　　　　　　 D．6人洗澡

第Ⅱ卷（非选择题　共100分）

	1,3,5

二、填空题(本大题共5小题，每小题5分，共25分.把答案填在答题卡的相应位置上.)

11．2008年奥运福娃贝贝、晶晶、欢欢、迎迎、妮妮排队，欢欢、迎迎排在一起的排法种数是______________（用数值作答）.

12．已知某天一工厂甲、乙、丙三个车间生产的产品件数分别是1500、1300、1200，现用分层抽样方法抽取了一个样本容量为n的样本，进行质量检查，已知丙车间抽取了24件产品，则n=___________.

13．已知直线与圆相切，则直线的倾斜角为____________.
14．将函数的图像按向量平移后得到函数的图象，则的坐标为_______.

15．已知函数y=f(x)满足，且在上为增函数，则、、按从大到小的顺序排列出来的是________________.

三、解答题(本大题共6小题，共75分.解答应写出文字说明，证明过程或演算步骤.)

16．(本小题满分12分)

甲、乙两人破译一种密码，它们能破译的概率分别为和，求：

（1）恰有一人能破译的概率；（2）至多有一人破译的概率；

（3）若要破译出的概率为不小于，至少需要多少甲这样的人？

17．(本小题满分12分)

在中，A、B、C所对边长分别是a, b, c，已知向量，满足，

（1）求A的大小；（2）求的值.

18．(本小题满分12分)

已知数列{a_n}的前n项和为S_n（），且

（1）求证：是等差数列；（2）求a_n；

（3）若，求证：

19．(本小题满分12分)

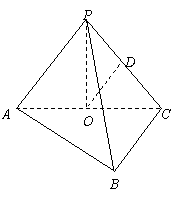在三棱锥P—ABC中，，点O、D分别是AC、PC的中点，

 底面ABC.

（1）求证OD∥平面PAB；

（2）求二面角A—BC—P的大小.

20．(本小题满分13分)

已知函数的图象经过原点，且在x=1处取得极值，直线到曲线在原点处的切线所成的角为45°.

（1）求的解析式；

（2）若对于任意实数和恒有不等式成立，求m的最小值.

21．(本小题满分14分)

已知一个椭圆的左焦点及相应的准线与抛物线的焦点F和准线l分别重合.

（1）求椭圆的短轴的端点与焦点F所连线段的中点M的轨迹方程；

（2）若P为点M的轨迹上一点，且Q(m, 0)为x轴上一点，讨论PQ的最小值.

参考答案

1,3,5

1.C  2.D  3.C　4.C  5.D　6.D　7.C  8.A　9.C　10.B

11．48　　　　　 12．80　　　　　 13．　　　　 14．（1，-2）　　　　　　 15．

16．（1）设A为“甲能译出”，B为“乙能译出”，则A、B互相独立，从而A与、与B、与均相互独立.

“恰有一人能译出”为事件，又与互斥，

则

（2）“至多一人能译出”的事件，且、、互斥，

∴

（3）设至少需要n个甲这样的人，而n个甲这样的人译不出的概率为，

∴n个甲这样的人能译出的概率为，

由

∴至少需4个甲这样的人才能满足题意.

17．（1）由得，所以，所以，因为A为的内角，所以

（2）因为，由正弦定理得

由（1）得所以∴

18．（1）∵，∴，又∵ ∴

∴数列是等差数列，且

（2）当时，

当n=1时，不成立. ∴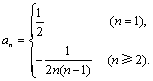

（3），∴.

∴左边显然成立.

19．（1）∵O、D分别为AC、PC的中点，∴OD∥PA. 又PA平面PAB，∴OD∥平面PAB.

（2）∵ 又∵平面ABC，∴PA=PB=PC，

取BC中点E，连结PE和OE，则

∴是所求二面角的平面角.

又，易求得 在直角中，，

∴二面角A—BC—P的大小为

20．（1）由题意有，且又曲线在原点处的切线的斜率 而直线到此切线所成的角为45°，

∴，解得b= -3.

代入得a=0，故f(x)的解析式为

（2）由可知，f(x)在和上递增；在[-1，1]上递减，又

∴f(x)在[-2，2]上的最大值和最小值分别为-2，2.

又∵、，

∴. 故，即m的最小值为4.

21．（1）由抛物线知焦点F（2，0），准线l的方程为x= -2，若椭圆的中心为，长半轴长，短半轴长，半焦距分别为a, b, c，准线l与x轴交于点N，

则　　　　　　①

设椭圆的短轴端点为B，且B的坐标为（），

BF的中点为，即，

又∵，代入①得，

它就是点M的轨迹方程.

（2）设为点M的轨迹上的一点，则

令，其图象为开口向上的抛物线，对称轴为直线，由于为点M轨迹上的点，则x>2，于是当，即时，f(x)无最小值，PQ也无最小值，当m-1>2，即m>3时，

∴当m>3时，