08级重庆名校高考理科数学4月测试试题
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分。考试时间120分钟。
第I卷(选择题 共50分)
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知集合![]() 则
则![]()
A ![]() B
B ![]() C
C ![]() D
D ![]()
2.设等比数列![]() 中,前
中,前![]() 项和为
项和为![]() ,已知
,已知![]() ,
,![]() ,则
,则![]()
A ![]() B
B ![]() C
C ![]() D
D ![]()
3.对于不重合的两个平面,给定下列条件:①存在直线![]() ,使
,使![]() ;②存在平面
;②存在平面![]() ,使
,使![]() ;③
;③![]() 内有不共线三点到
内有不共线三点到![]() 的距离相等;④存在异面直线
的距离相等;④存在异面直线![]() ,
,![]() 使
使![]() 。其中可以判定
。其中可以判定![]() 的有( )个
的有( )个
A 1 B 2 C 3 D 4
4.把函数![]() 的图象按向量
的图象按向量![]() 平移得到
平移得到![]() 的图象 则
的图象 则![]() =
=
A ![]() B
B ![]() C
C ![]() D
D ![]()
5.在平面直角坐标系中,双曲本线的中心在原点,焦点在![]() 轴上,一条渐近线方程为
轴上,一条渐近线方程为![]() ,则它的离心率为:
,则它的离心率为:
A ![]() B
B ![]() C
C ![]() D
3
D
3
6.已知![]() 的展开式中,二项式系数和为
的展开式中,二项式系数和为![]() ,各项系数和为
,各项系数和为![]() ,则
,则![]()
A ![]() B
B ![]() C -3 D 3
C -3 D 3
7.已知函数![]() 的值域为R,则
的值域为R,则![]() 的取值范围是:
的取值范围是:
A ![]() B
B ![]() C
C ![]() D
D ![]()
8.如果椭圆![]() 上存在一点P,使点P到左准线的距离与它到右焦点的距离相等,那么椭圆的离心率的范围是。
上存在一点P,使点P到左准线的距离与它到右焦点的距离相等,那么椭圆的离心率的范围是。
A ![]() B
B ![]() C
C ![]() D
D ![]()
9.已知⊿ABC,若对任意![]() ,
,![]() 恒成立,⊿ABC则必定为
恒成立,⊿ABC则必定为
A 锐角三角形 B 钝角三角形 C 直角三角形 D 不确定
10.过正方体任意两个顶点的直线共有28条,其中异面直线有( )对
A 32 B 72 C 174 D 189
第Ⅱ卷(非选择题 共100分)
二、填空题(本大题共5小题,每小题5分,共25分。把答案填在题中横线上。)
11.若复数Z满足关系式![]() ,则Z的共轭复数为
,则Z的共轭复数为
12.![]() 的二项式展开式中的
的二项式展开式中的![]() 系数是
系数是
13.一次测量中,出现正误差和负误差的概率均为![]() ,那么在5次测量中,至少3次正误差的概率是
,那么在5次测量中,至少3次正误差的概率是
14设函数![]() ,若函数
,若函数![]() 是奇函数,则
是奇函数,则![]() =
=
![]()
![]()
15.设 ![]()
![]()
![]()
![]()
若非![]() 是非
是非![]() 的充分必要条件,那么
的充分必要条件,那么![]() 是
是![]() 的
条件,的取值范围为 .
的
条件,的取值范围为 .
三、解答题(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤)
16.(本小题满分12分)
已知![]()
(1)
求函数![]() 值域
值域
(2)
若对任意的![]() ,函数
,函数![]() 在
在![]() 上的图象与
上的图象与![]() 有且仅有两个不同
有且仅有两个不同
的交点,试确定![]() 的值(不必证明)并写出该函数在
的值(不必证明)并写出该函数在![]() 上的单调区间。
上的单调区间。
17.箱子中装有大小相同的2个红球、8个黑球,每次从中摸取1个球。每个球被取到可能性相同。
(1)若每次取球后不放回,求取出3个球中至少有1个红球的概率。
(2)若每次取出后再放回,求第一次取出红球时,已取球次数的分布及数学期望。(要求写出期望过程)
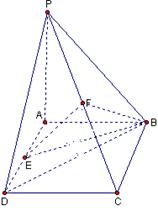
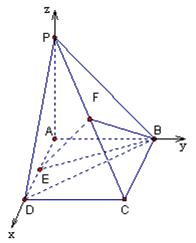
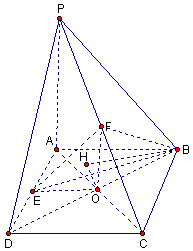
18.如图,在四棱锥P-ABCD中,底面是矩形,且![]() ,
,![]() ,
,![]() 底面ABCD,E为AD的中点,F为PC的中点.
底面ABCD,E为AD的中点,F为PC的中点.
(1)求证:EF为AD及PC的公公垂线
(2)求直线BD与平面BEF所成的角。
19.数列![]() 是一个首项为4,公比为2的等比数,
是一个首项为4,公比为2的等比数,![]() 是
是![]() 的前
的前![]() 项和。
项和。
(1)求数列![]() 的通项及
的通项及![]()
(2)设点列![]() 试求出一个半径最小的圆,使点列
试求出一个半径最小的圆,使点列![]() 中任何一个点都不在该圆外部
中任何一个点都不在该圆外部
20.⊿ABC的内切圆与三边AB、BC、CA的切点分别为D、E、F,已知![]() ,内切圆圆心
,内切圆圆心![]() ,设点A的轨迹为L
,设点A的轨迹为L
(1) 求L的方程
(2)
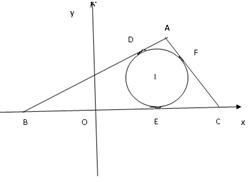 过点C作直线交曲线L于不同两点M、N,问在
过点C作直线交曲线L于不同两点M、N,问在![]() 轴上是否存在异于C点的点Q,使
轴上是否存在异于C点的点Q,使![]() 对任意的直线
对任意的直线![]() 成立,若存在,试求出点Q的坐标,若不存在,说明理由。
成立,若存在,试求出点Q的坐标,若不存在,说明理由。
21.已知![]() 其中
其中![]() 是自然常数,
是自然常数,![]()
(1)讨论![]() 时,
时, ![]() 的单调性、极值;
的单调性、极值;
(2)求证:在(1)的条件下,![]()
(3)是否存在实数![]() ,使
,使![]() 的最小值是3,如果存在,求出
的最小值是3,如果存在,求出![]() 的值;如果不存在,说明理由。
的值;如果不存在,说明理由。
参考答案
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | B | B | C | A | C | D | B | C | C |
二、填空题:
11、![]() 12、560 13、
12、560 13、![]() 14、
14、![]() 15、充分非必要
15、充分非必要 ![]()
三、解答题:
16、(1)![]()
![]()
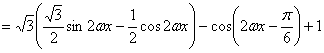
![]() (2分)
(2分)
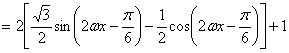
![]() (6分)
(6分)
![]()
![]() 值域为
值域为![]() (不同变形参照给分)
(不同变形参照给分)
(2)因为![]() 周期为
周期为![]()
![]()
![]() (8分)
(8分)
![]()
![]() 在
在![]() 、
、![]() 上单调递增,在
上单调递增,在![]() 上单调递减。
上单调递减。
(12分)
17、(1)![]() (4分)
(4分)
![]()
![]()
(2)分布列为:
|
| 1 | 2 | 3 | … |
| … |
|
|
|
|
| … |
| … |
(7分 没写后面省略号扣1分)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
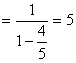
(12分
直接用![]() 计算只给2分)
计算只给2分)
 18、方法一:
18、方法一:
设![]() ,则
,则![]()
(1)![]()
![]()
![]()
![]()
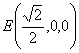
![]()
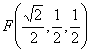
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
故![]() 为
为![]() 及
及![]() 的公垂线
(6分)
的公垂线
(6分)
(2)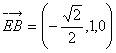
![]()
![]()
![]()
![]()
![]() 故
故![]() 可看成平面
可看成平面![]() 的法向量
的法向量
 故
故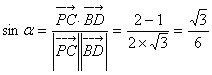 (12分)
(12分)
方法二:
(1)连![]() 、
、![]() 、
、![]() 、
、![]()
![]()
![]()
![]()
又![]()
![]()
![]()
![]()
![]()
又![]()
![]() 为
为![]() 的中点
的中点
![]()
![]()
又![]()
![]() ∥
∥![]()
![]()
![]()
而![]()
![]()
![]()
故![]() 为
为![]() 及
及![]() 的公垂线
(6分)
的公垂线
(6分)
(2)过![]() 作
作![]() 于
于![]() ,连
,连![]() ,
,![]() 为所求
为所求![]() 与平面
与平面![]() 所成的角
(8分)
所成的角
(8分)
设![]()
![]()
![]()
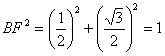
![]()
![]()
![]()
![]()
![]() (10分)
(10分)
![]()
![]()
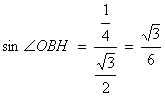 (12分)
(12分)
(其它解法参照给分)
19、(1)![]()
![]()
![]()
![]()
![]()
![]()
![]()
即![]() 故
故![]() 是以1为首项,
是以1为首项,![]() 为公差的等差数列 (3分)
为公差的等差数列 (3分)
![]()
![]()
![]() (5分)
(5分)
(2)设![]()
![]()
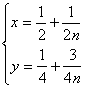
由此可得![]() 在直线
在直线![]() 上
(8分)
上
(8分)
横坐标、纵坐标随![]() 的增大而减小,并与
的增大而减小,并与![]() 无限接近,故所求圆就是以
无限接近,故所求圆就是以![]() 、
、![]() 为直径端点的圆
为直径端点的圆
即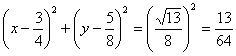 (12分)
(12分)
20、(1)由题知![]()
根据双曲线定义知,点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点,实轴长为2的双曲线的右支除去点
为焦点,实轴长为2的双曲线的右支除去点![]() ,故
,故![]() 的方程为
的方程为![]() (
(![]() ) (5分)
) (5分)
(2)设点![]() 、
、![]() 、
、![]() ,由(1)可知
,由(1)可知![]()
![]()
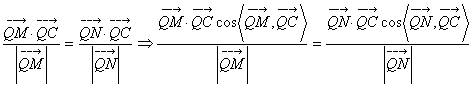
![]()
![]()
![]()
![]() (7分)
(7分)
①当直线![]()
![]()
![]() 轴时,点
轴时,点![]() 在
在![]() 轴上任何一点处都能使得
轴上任何一点处都能使得![]() 成立
成立
②当直线![]() 不与
不与![]() 轴垂直时,设直线
轴垂直时,设直线![]() :
:![]()
由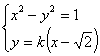 得
得![]()
![]()
![]()
![]() (9分)
(9分)
![]()
![]()
![]()
![]()
要使![]() ,只需
,只需![]() 成立
成立
即![]() 即
即![]() (11分)
(11分)
![]()
![]()
即![]() 故
故![]()
故所求的点![]() 的坐标为
的坐标为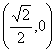 时,使
时,使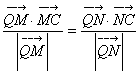 成立
成立
(13分)
21、(1)![]()
![]()
![]()
![]() 当
当![]() 时,
时,![]() ,此时
,此时![]() 为单调递减
为单调递减
当![]() 时,
时,![]() ,此时
,此时![]() 为单调递增
为单调递增
![]()
![]() 的极小值为
的极小值为![]() (4分)
(4分)
(2)![]()
![]() 的极小值,即
的极小值,即![]() 在
在![]() 的最小值为1
的最小值为1
![]()
![]() 令
令![]()
又![]()
![]() 当
当![]() 时
时![]()
![]() 在
在![]() 上单调递减
上单调递减
![]()
![]() (8分)
(8分)
![]() 当
当![]() 时,
时,![]()
(3)假设存在实数![]() ,使
,使![]() 有最小值3,
有最小值3,![]()
![]()
①当![]() 时,由于
时,由于![]() ,则
,则![]()
![]() 函数
函数![]() 是
是![]() 上的增函数
上的增函数
![]()
![]()
解得![]() (舍去)
(10分)
(舍去)
(10分)
②当![]() 时,则当
时,则当![]() 时,
时,![]()
此时![]() 是减函数
是减函数
当![]() 时,
时,![]() ,此时
,此时![]() 是增函数
是增函数
![]()
![]()
解得![]() (13分)
(13分)
由①、②知,存在实数![]() ,使得当
,使得当![]() 时
时![]() 有最小值3
有最小值3
(14分)