高考理科数学复习第三次月考试卷
第Ⅰ卷
一.选择题:(每小题5分,共40分)
1.若对任意![]() ,不等式
,不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.椭圆![]() 的离心率为( )
的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. 设方程![]() 的解集为A,方程
的解集为A,方程![]() 的解集为B,若
的解集为B,若![]() ,
,
则p+q= ( )
A、2 B、0 C、1 D、-1
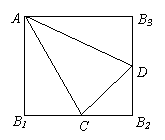 4.如图,正方形AB1 B2 B3中,C,D分别是B1 B2 和B2 B3
4.如图,正方形AB1 B2 B3中,C,D分别是B1 B2 和B2 B3
的中点,现沿AC,AD及CD把这个正方形折成一个四面体,
使B1 ,B2 ,B3三点重合,重合后的点记为B,则四面体
A—BCD中,互相垂直的面共有( )
A.4对 B.3对
C.2对 D.1对
5.某通讯公司推出一组手机卡号码,卡号的前七位数字固定,从“![]() ”到“
”到“![]() ”共
”共![]() 个号码.公司规定:凡卡号的后四位带有数字“
个号码.公司规定:凡卡号的后四位带有数字“![]() ”或“
”或“![]() ”的一律作为“优惠卡”,则这组号码中“优惠卡”的个数为( )
”的一律作为“优惠卡”,则这组号码中“优惠卡”的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.对于![]() 上可导的任意函数
上可导的任意函数![]() ,若满足
,若满足![]() ,则必有( )
,则必有( )
A.![]() B.
B.
![]()
C.![]() D.
D.![]()
7.在平面直角坐标系![]() 中,已知平面区域
中,已知平面区域![]() ,则平面区域
,则平面区域![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.设![]() 是奇函数,则使
是奇函数,则使![]() 的
的![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 二.填空题:(每小题5分,共30分)
二.填空题:(每小题5分,共30分)
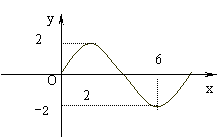
9. 函数![]() 的部分图象
的部分图象
如图所示,则![]()
10.若向量![]() 、
、![]() 的坐标满足
的坐标满足![]()
![]() ,
,![]()
![]() ,则
,则![]() ·
·![]() 等于
等于
11、![]() 。
。
12.等比数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() ,
,![]() ,
,![]() 成等差数列,则
成等差数列,则![]() 的公比为 .
的公比为 .
选做题:在下面三道小题中选做两题,三题都选只计算前两题的得分.
13.过点A(2,3)的直线的参数方程![]() ,若此直线与直线
,若此直线与直线![]()
相交于点B,则![]() = 。
= 。
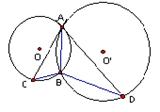
|
的切线,交⊙O于点C,AD是⊙O的切线,交⊙![]() 于
于
点D,若BC= 2,BD=6,则AB的长为
15.设![]() ,则
,则![]() 的最小值为_____________。
的最小值为_____________。
三.解答题:
16.(本小题满分12分)
已知函数![]() .
.
(Ⅰ)求函数![]() 的最小正周期;
的最小正周期;
(Ⅱ)求函数![]() 在区间
在区间![]() 上的最小值和最大值.
上的最小值和最大值.
17.(本小题满分12分)
从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件![]() :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率![]() .
.
(1)求从该批产品中任取1件是二等品的概率![]() ;
;
(2)若该批产品共100件,从中任意抽取2件,![]() 表示取出的2件产品中二等品的件数,求
表示取出的2件产品中二等品的件数,求![]() 的分布列.
的分布列.
18.(本小题满分14分)
设数列![]() 满足
满足![]() ,
,![]() .
.
(Ⅰ)求数列![]() 的通项;
的通项;
(Ⅱ)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
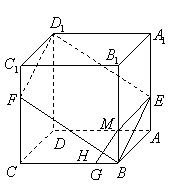 19.(本题满分14分)
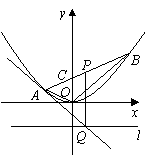
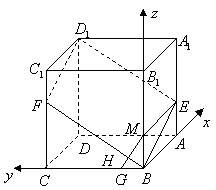
19.(本题满分14分)
如图,已知![]() 是棱长为
是棱长为![]() 的正方体,
的正方体,
点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() .
.
(1)求证:![]() 四点共面;(4分)
四点共面;(4分)
(2)若点![]() 在
在![]() 上,
上,![]() ,点
,点![]() 在
在![]() 上,
上,
![]() ,垂足为
,垂足为![]() ,求证:
,求证:![]() 平面
平面![]() ;(4分)
;(4分)
(3)用![]() 表示截面
表示截面![]() 和侧面
和侧面![]() 所成的锐二面角的大小,求
所成的锐二面角的大小,求![]() .(4分)
.(4分)
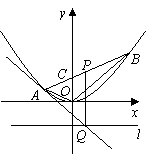
 20.(本题满分14分)
20.(本题满分14分)
如图,在平面直角坐标系![]() 中,过
中,过![]() 轴正方向上一点
轴正方向上一点![]() 任作一直线,与抛物线
任作一直线,与抛物线![]() 相交于
相交于![]() 两点.一条垂直于
两点.一条垂直于![]() 轴的直线,分别与线段
轴的直线,分别与线段![]() 和直线
和直线![]() 交于点
交于点![]() .
.
(1)若![]() ,求
,求![]() 的值;(5分)
的值;(5分)
(2)若![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() 为此抛物线的切线;(5分)
为此抛物线的切线;(5分)
(3)试问(2)的逆命题是否成立?说明理由.(4分)
21.(本小题满分14分)
设函数![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,判断函数
时,判断函数![]() 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)求函数![]() 的极值点;
的极值点;
(Ⅲ)证明对任意的正整数![]() ,不等式
,不等式![]() 都成立.
都成立.
2007~2008学年度第一学期

答题卷(II)
一.选择题(每小题5分,共40分)
| 题序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 |
|
|
|
|
|
|
|
|
二、填空题(每小题5分,共30分):
9.___________;10.___________;11.______________________;
12._____________________;13._____________________;
14.____________________;15._____________________
三、解答题:(共80分,要求写出解答过程)
16.(本小题满分12分)
17.(本小题满分12分)
18.(本小题满分14分)
19.(本小题满分14分)
 20.(本小题满分14分)
20.(本小题满分14分)
21.(本小题满分14分)

参考答案
一.选择题(每小题5分,共40分)
| 题序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | B | A | C | C | C | B | B | A |
二、填空题(每小题5分,共30分):
9.__ ![]() _________;10.___ -5________;11.______
_________;10.___ -5________;11.______ ![]() ________________;
________________;
12._________ ![]() ____________;13.________
____________;13.________ ![]() _____________;
_____________;
14.________![]() ____________;15.________
____________;15.________ ![]() _____________
_____________
三.解答题:
16.(Ⅰ)解:![]() .
.
因此,函数![]() 的最小正周期为
的最小正周期为![]() .
.
(Ⅱ)解法一:因为![]() 在区间
在区间![]() 上为增函数,在区间
上为增函数,在区间![]() 上为减函数,又
上为减函数,又![]() ,
,![]() ,
,![]() ,
,
故函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() .
.
17.解:(1)记![]() 表示事件“取出的2件产品中无二等品”,
表示事件“取出的2件产品中无二等品”,
![]() 表示事件“取出的2件产品中恰有1件二等品”.
表示事件“取出的2件产品中恰有1件二等品”.
则![]() 互斥,且
互斥,且![]() ,故
,故
![]()
于是![]() .
.
解得![]() (舍去).
(舍去).
(2)![]() 的可能取值为
的可能取值为![]() .
.
若该批产品共100件,由(1)知其二等品有![]() 件,故
件,故
![]() .
.
![]() .
.
![]() .
.
所以![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 |
|
|
|
|
|
18. 解:(Ⅰ)![]() , ①
, ①
![]() 当
当![]() 时,
时,![]() . ②
. ②
①-②得![]() ,
,![]() .
.
在①中,令![]() ,得
,得![]() .
.
![]() .
.
(Ⅱ)![]() ,
,
![]() .
.
![]() , ③
, ③
![]() .
④
.
④
④-③得
![]() .
.
即![]() ,
,
![]() .
.
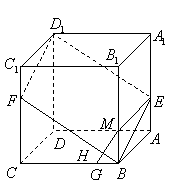
19.(1)如图,在![]() 上取点
上取点![]() ,使
,使![]() ,连结
,连结![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
因为![]() ,
,![]() ,所以四边形
,所以四边形![]() ,
,![]() 都为平行四边形.
都为平行四边形.
从而![]() ,
,![]() .
.
又因为![]() ,所以
,所以![]() ,故四边形
,故四边形![]() 是平行四边形,由此推知
是平行四边形,由此推知![]() ,从而
,从而![]() .
.
因此,![]() 四点共面.
四点共面.
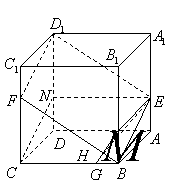
(2)如图,![]() ,又
,又![]() ,所以
,所以![]() ,
,
![]()
![]() .
.
因为![]() ,所以
,所以![]() 为平行四边形,从而
为平行四边形,从而![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(3)如图,连结![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,得
,得![]() .
.
于是![]() 是所求的二面角的平面角,即
是所求的二面角的平面角,即![]() .
.
因为![]() ,所以
,所以![]()
![]() ,
,
![]() .
.
解法二:
(1)建立如图所示的坐标系,则![]() ,
,![]() ,
,![]() ,
,
所以![]() ,故
,故![]() ,
,![]() ,
,![]() 共面.
共面.
 又它们有公共点
又它们有公共点![]() ,所以
,所以![]() 四点共面.
四点共面.
(2)如图,设![]() ,则
,则![]() ,
,
而![]() ,由题设得
,由题设得![]() ,
,
得![]() .
.
因为![]() ,
,![]() ,有
,有![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,从而
,从而![]() ,
,![]() .
.
故![]() 平面
平面![]() .
.
(3)设向量![]() 截面
截面![]() ,于是
,于是![]() ,
,![]() .
.
而![]() ,
,![]() ,得
,得![]() ,
,![]() ,解得
,解得![]() ,
,![]() ,所以
,所以![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() 和
和![]() 的夹角等于
的夹角等于![]() 或
或![]() (
(![]() 为锐角).
为锐角).
 于是
于是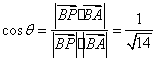 .
.
故![]() .
.
20.解:(1)设直线![]() 的方程为
的方程为![]() ,
,
将该方程代入![]() 得
得![]() .
.
令![]() ,
,![]() ,则
,则![]() .
.
因为![]() ,解得
,解得![]() ,
,
或![]() (舍去).故
(舍去).故![]() .
.
(2)由题意知![]() ,直线
,直线![]() 的斜率为
的斜率为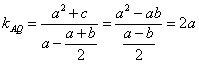 .
.
又![]() 的导数为
的导数为![]() ,所以点
,所以点![]() 处切线的斜率为
处切线的斜率为![]() ,
,
因此,![]() 为该抛物线的切线.
为该抛物线的切线.
(3)(2)的逆命题成立,证明如下:
设![]() .
.
若![]() 为该抛物线的切线,则
为该抛物线的切线,则![]() ,
,
又直线![]() 的斜率为
的斜率为![]() ,所以
,所以![]() ,
,
得![]() ,因
,因![]() ,有
,有![]() .
.
故点![]() 的横坐标为
的横坐标为![]() ,即
,即![]() 点是线段
点是线段![]() 的中点.
的中点.
21.解:(Ⅰ)由题意知,![]() 的定义域为
的定义域为![]() ,
,![]()
设![]() ,其图象的对称轴为
,其图象的对称轴为![]() ,
,
![]() .
.
当![]() 时,
时,![]() ,
,
即![]() 在
在![]() 上恒成立,
上恒成立,
![]() 当
当![]() 时,
时,![]() ,
,
![]() 当
当![]() 时,函数
时,函数![]() 在定义域
在定义域![]() 上单调递增.
上单调递增.
(Ⅱ)①由(Ⅰ)得,当![]() 时,函数
时,函数![]() 无极值点.
无极值点.
②![]() 时,
时,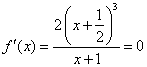 有两个相同的解
有两个相同的解![]() ,
,
![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,
,
![]() 时,函数
时,函数![]() 在
在![]() 上无极值点.
上无极值点.
③当![]() 时,
时,![]() 有两个不同解,
有两个不同解,![]() ,
,![]() ,
,
![]() 时,
时,![]() ,
,![]() ,
,
即![]() ,
,![]() .
.
![]() 时,
时,![]() ,
,![]() 随
随![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
|
由此表可知:![]() 时,
时,![]() 有惟一极小值点
有惟一极小值点![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,
此时,![]() ,
,![]() 随
随![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
| 极小值 |
|
由此表可知:![]() 时,
时,![]() 有一个极大值
有一个极大值![]() 和一个极小值点
和一个极小值点![]() ;
;
综上所述:
![]() 时,
时,![]() 有惟一最小值点
有惟一最小值点![]() ;
;