08年上海市高考理科数学十校联考试卷
一、填空题. （本大题满分44分）本大题共有11题，只要求直接填写结果，每个空格填对得4分，否则一律得零分．
1．已知集合
，函数
的定义域为B，则
________
2．不等式
的解集为___________.
3. 函数y=1og2(x2+2)(x≤0)的反函数是_________________.
4．已知复数
且
是实数，则实数
5．函数
的最小正周期是____________.
6．以抛物线
的焦点
为右焦点,且两条渐近线是
的双曲线方程为___________________.
7.在极坐标系中，点
到圆
上动点的距离的最大值为________.
8. 函数
则方程
的实根的个数是_________.
9．特奥会期间，某高校有14名志愿者参加接待工作．若每天排早、中、晚三班，每班4人，每人每天最多值一班，则开幕式当天不同的排班种数为___________.
10．设
是
其中
分别是
的最小值是_______________.
11．已知
是定义在
上的不恒为零的函数，且对于任意的
，满足
,
考查下列结论：（1）
；（2）为偶函数；（3）数列
为等比数列；（4）
。其中正确的是__________。
二、选择题. （本大题满分16分）本大题共有4 题，每题都给出代号为A，B，C，D的四个结论，其中有且只有一个结论是正确的。
12. 
(
)
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要。
13．已知函数
的图象按向量
平移得到函数
的图象，则函数
的反函数
的图象恒过定点 （
）
A．（2，1） B．（1，2） C．（－2，1） D．（0，2）
14．已知直线m、n及平面
，其中m∥n，那么在平面内到两条直线m、n距离相等的点的集合可能是：（1）一条直线；（2）一个平面；（3）一个点；（4）空集。其中正确的是（ ）
A、（1）（2）（3） B、（1）（4） C、（1）（2）（4） D、（2）（4）
15.一机器猫每秒钟前进或后退一步，程序设计师让机器猫以前进3步，然后再后退2步的规律移动。如果将此机器猫放在数轴的原点，面向正方向，以1步的距离为1单位长移动。令P（n）表示第n秒时机器猫所在位置的坐标，且P（0）=0，则下列结论中错误的是 （ ）
A．P（3）=3 B．P（5）=1 C．P（101）=21 D．P（101）> P（104）
三、解答题。（本大题满分90分）本大题共有6题，解答下列各题必须写出必要的步骤．
16．（本题满分12分）已知
是
中
的对边，若
求边长
及外接圆半径
17．（本题满分14分）
直三棱柱ABC-A1B1C1的底面为等腰直角三角形，
BAC=900，AB=AC=2，AA
=2
，E, F分别是BC、AA1的中点。求（1）异面直线EF和A1B所成的角。
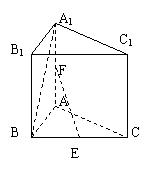（2）直三棱柱ABC-A1B1C1的体积。
18. （本题满分14分）某地区由于战争的影响，据估计，将产生60~100万难民，联合国难民署从4月1日起为该地区难民运送食品. 连续运送15天，总共运送21300 t；第一天运送1000 t，第二天运送1100 t，以后每天都比前一天多运送100 t，直到达到运送食品的最大量，然后再每天递减100 t；求在第几天达到运送食品的最大量.
19. （本题满分14分）已知函数
（常数
）
(1)求函数的定义域，判断的奇偶性并说明理由.
(2)试研究函数在定义域内的单调性，并利用单调性的定义给出证明。
20. （本题满分18分）已知F1、F2分别是椭圆
的左、右焦点，P是此椭圆上的一动点，并且
的取值范围是
(1) 求此椭圆的方程；
(2) 点A是椭圆的右顶点，直线y = x与椭圆交于B、C两点(C在第一象限内)，又P、Q是椭圆上两点，并且满足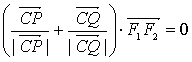
，求证：向量
共线．
21．（本题满分18分）
已知向量
,其中
,
,
把其中
所满足的关系式记为
,若函数
为奇函数.
(Ⅰ) 求函数的表达式；
(Ⅱ) 已知数列
的各项都是正数, 
为数列的前
项和,且对于任意
,都有“
的前项和等于
,”求数列的通项式；
(Ⅲ) 若数列
满足
,求数列的最小值.
答题纸（理）
一、填空题.（（本大题满分44分）
| 1． | 2． | 3． | 4． |
| 5． | 6． | 7． | 8． |
| 9． | 10． | 11． |
二、选择题. （本大题满分16分）
| 12． | 13． | 14． | 15． |
三、解答题。（本大题满分90分）
16．
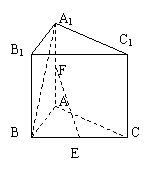17．
18．
19．
20．
|
21．
答题纸（理）
一、填空题.（本大题满分44分）
| 1． | 2． | 3． | 4． |
| 5． | 6． | 7． | 8． 2个 |
| 9． | 10． 18 | 11．①③④ |
(x≥1)
二、选择题. （本大题满分16分）
| 12． A | 13．B | 14．C | 15．D |
三、解答题。（本大题满分90分）
16． 解：
……6分
由正弦定理:
中
……6分
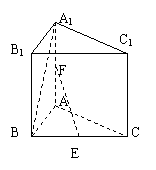17. 解：（1）方法一：取AB的中点D，连DE、DF，
则
∥
，
∴∠DFE（或其补角）即为所求。……3分
由题意易知，
，
，
由DE⊥AB、DE⊥A A1得DE⊥平面ABB1A1
∴DE⊥DF，即△EDF为直角三角形，……3分
∴
∴
……3分
即异面直线EF和A1B所成的角为
。 ……1分
方法二：
以A为坐标原点以AB、AC、AA1所在直线分别x轴、y轴、
Z轴建立如图所示的直角坐标系， ……1分
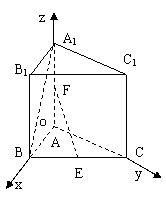则A1 (o,o,2) B (2,0,0)
E、F分别是BC、AA1中点
∴E(1,1,0) F(0,0,)
……4分
∴
，
设
的夹角为
∴cos=
∴ 
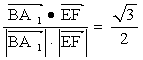
……4分
∴异面直线EF和A1B所成的角为
……1分
（2）直三棱柱ABC-A1B1C1的体积
……4分
18.解：设在第n天达到运送食品的最大量.
则前n天每天运送的食品量是首项为1000，公差为100的等差数列.
an=1000+（n－1）·100=100n+900.。 ……3分
其余每天运送的食品量是首项为100n+800，公差为－100的等差数列.
……3分
依题意，得
1000n+
×100+（100n+800）（15－n）+
×（－100）=21300（1≤n≤15）. ……5分
整理化简得n2－31n+198=0.
解得n=9或22（不合题意，舍去）. ……2分
答：在第9天达到运送食品的最大量. ……1分
19. 解：（1）定义域为：
……2分
是偶函数，
…2分
（2）
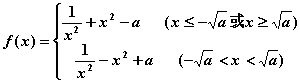
若
，
当
时，
在
上是增函数；
又是偶函数，在
上是减函数。
……3分
当
时，
时,
时,
在
上是减函数，在
上是增函数；
又是偶函数，在
上是增函数，在
上是减函数。 ……3分
若
上是减函数，
又是偶函数，于是在
上是增函数。 ……3分
由可知：当
时，在
上是减函数，在上是增函数，
在上是减函数，在
上是增函数；
当
时， 在
上是减函数，在上是增函数，
在上是减函数，在上是增函数。
……1分
20. 解：(1) 设
，
其中
，
从而
……4分
由于
，
即
又已知
，
所以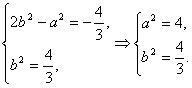
从而椭圆的方程是
……4分
(2) 因为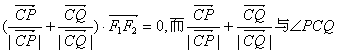
的平分线平行，
所以∠PCQ的平分线垂直于x轴. ……2分
由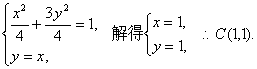
不妨设PC的斜率为k，则QC的斜率为-k，因此PC和QC的方程分别为
，
其中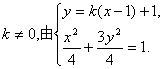
消去y并整理得
……3分
∵C(1，1) 在椭圆上，∴x = 1是方程(*) 的一个根.
从而
，
……2分
从而直线PQ的斜率为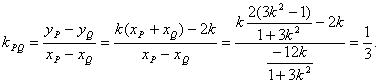
又知A(2，0) ，B(－1，－1) ，
所以
共线。 ……3分
21．解：(Ⅰ) 
,因为函数为奇函数.所以
,
…………4分
(Ⅱ)由题意可知,
…..①
………②
由①-②可得:
,
为正数数列
③
……2分
④
由④-③可得: 
……2分
且由①可得
，
为公差为1的等差数列,
……2分
(Ⅲ) 
,
……2分
令
,
(1)当
时,数列的最小值为：当
时, 
……2分
(2)当
时
①若
时,数列的最小值为当
时,
……1分
②若
时,数列的最小值为, 当
或
时，
. …1分
③若
时, 数列的最小值为, 当 时,
……1分
④若
时,数列的最小值为, 当
时，
.……1分