08年咸阳市高考数学第一次模拟考试
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.
参考公式:
如果事件A、B互斥,那么
P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么
P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率
![]()
正棱锥、圆锥的侧面积公式S锥体侧S锥体侧=![]() 其中c表示底面周长, l表示斜高或母线长.
其中c表示底面周长, l表示斜高或母线长.
球的体积公式
球![]() 球=
球= ![]() 其中R表示球的半径.
其中R表示球的半径.
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合![]() ={
={![]() },
}, ![]() ,则
,则![]() 为 ( )
为 ( )
A.![]() B.
B.![]() C.{1} D.{(
C.{1} D.{(![]() )}
)}
2.若函数![]() 的定义域是
的定义域是![]() ,则其值域为
( )
,则其值域为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]()
3.O是平面上一定点,A,B,C是平面上不共线的三个点,动点P满足![]() ,λ∈[0,+∞),则P的轨迹一定通过△ABC的
( )
,λ∈[0,+∞),则P的轨迹一定通过△ABC的
( )
A.外心 B.垂心 C.内心 D.重心
4.在坐标平面上,不等式组![]() 所表示的平面区域的面积为
( )
所表示的平面区域的面积为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.全国十运会期间,某高校有14名志愿者参加接待工作.若每天排早、中、晚三班,每班4人,每人每天最多值一班,则开幕式当天不同的排班种数为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.对于不重合的两个平面![]() ,给定下列条件:
,给定下列条件:
①存在平面![]() ,使得
,使得![]() 都垂直于
都垂直于![]() ;
;
②存在平面![]() ,使得
,使得![]() 都平行于
都平行于![]() ;
;
③存在直线![]() ,直线
,直线![]() ,使得
,使得![]() ;
;
④存在异面直线l、m,使得![]()
其中,可以判定α与β平行的条件有 ( )
A.1个 B.2个 C.3个 D.4个
7.已知首项为正数的等差数列{an}满足:a2005+a2006>0,a2005·a2006<0,则使前项Sn>0成立的最大自然数n是 ( )
A. 4009 B.4010 C. 4011 D.4012
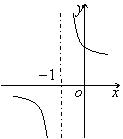
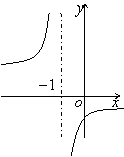 8. 函数
8. 函数![]() 的反函数图像大致是
( )
的反函数图像大致是
( )
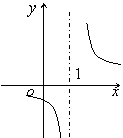
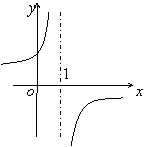
A B C D
9. 在正方体ABCD-A1B1C1D1中,E、F分别为A1D1、B1C1的中点,则在面BCC1B1内到BC的距离是到EF的距离的2倍的点的轨迹是( )
A.一条线段 B.椭圆的一部分 C.抛物线的一部分 D.双曲线的一部分.
10.已知F1、F2是双曲线![]() 的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是 ( )
的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知函数![]() 在
在![]() 上恒正,则实数
上恒正,则实数![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C. ![]()
![]()
![]() D.
D. ![]()
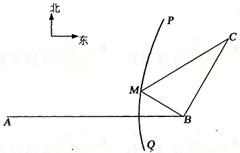 12. 如图,B地在A地的正东方向4 km处,C
12. 如图,B地在A地的正东方向4 km处,C
地在B地的北偏东30°方向2 km处,河流
的没岸PQ(曲线)上任意一点到A的距离
比到B的距离远2 km.现要在曲线PQ上
选一处M建一座码头,向B、C两地转运
货物.经测算,从M到B、M到C修建公
路的费用分别是a万元/km、2a万元/km,
那么修建这两条公路的总费用最低是( )
A.(2![]() -2)a万元 B.5a万元
-2)a万元 B.5a万元
C.(2![]() +1)
a万元 D.(2
+1)
a万元 D.(2![]() +3)
a万元
+3)
a万元
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题4个小题,每小题4分,共16分.
13.已知函数f(x)=Acos2(ωx+![]() )+1(A>0,ω>0)的最大值为3,f(x)的图象在y轴上的截距为2,其相邻两对称轴间的距离为2,则f(1)+f(2)+f(3)+…+f(100)=____________
)+1(A>0,ω>0)的最大值为3,f(x)的图象在y轴上的截距为2,其相邻两对称轴间的距离为2,则f(1)+f(2)+f(3)+…+f(100)=____________
14. 设点P是曲线y=x3-![]() x+2上的任意一点,P点处切线倾斜角为α,则角α的取值范围是______________
x+2上的任意一点,P点处切线倾斜角为α,则角α的取值范围是______________
15. 已知![]() 的展开式中
的展开式中![]() 的系数与
的系数与![]() 的展开式中
的展开式中![]() 的系数相等,则
的系数相等,则![]() =_____________.
=_____________.
16.若函数![]() 满足:对于任意
满足:对于任意![]() 都有
都有![]() ,
,![]() 且
且![]() 成立,则称函数
成立,则称函数![]() 具有性质M.
具有性质M.
给出下列四个函数:①![]() ,②
,②![]() ③
③![]() ,④
,④![]() .
.
其中具有性质M的函数是 (注:把满足题意的所有函数的序号都填上)
17.如图,在杨辉三角中,斜线l上方,从1开始箭头所示的数组成一个锯齿数列:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S19等于____________.
1
1 1 l
![]() 1 2 1
1 2 1
![]()
![]() 1 3 3 1
1 3 3 1
![]()
![]() 1 4 6 4 1
1 4 6 4 1
![]()
![]() 1 5 10 10 5 1
1 5 10 10 5 1
… … … … … … …
 18. 已知f(x+y)=f(x)·f(y)对任意的实数x、y都成立,且f(1)=2,则+++…++=
___________________.
18. 已知f(x+y)=f(x)·f(y)对任意的实数x、y都成立,且f(1)=2,则+++…++=
___________________.
三、解答题:本大题6小题,共74分,解答应写出必要的文字说明.推理过程或计算步骤.
19.(本题满分12分)
已知向量![]() (
(![]() ) 和
) 和![]() =(
=(![]() ),
),![]() ∈[π,2π].
∈[π,2π].
(Ⅰ)求![]() 的最大值;(Ⅱ)当
的最大值;(Ⅱ)当![]() =
=![]() 时,求
时,求![]() 的值.
的值.
20.(本小题满分12分)
甲、乙两人在一场五局三胜制的象棋比赛中,规定甲或乙无论谁先赢满三局就获胜,并且比赛就此结束.现已知甲、乙两人每比赛一局甲取胜的概率是![]() ,乙取胜的概率为
,乙取胜的概率为![]() ,且每局比赛的胜负是独立的,试求下列问题:
,且每局比赛的胜负是独立的,试求下列问题:
(Ⅰ)比赛以甲3胜1而结束的概率;
(Ⅱ)比赛以乙3胜2而结束的概率;
(Ⅲ)设甲获胜的概率为a,乙获胜的概率为b,求a:b的值.
21.(本题满分14分)
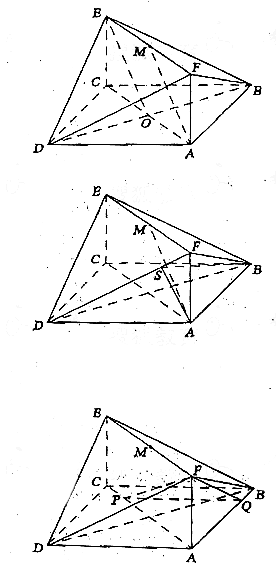
如图,已知正方形ABCD和矩形ACEF所在平面互相垂直,
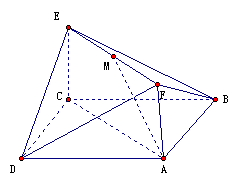 AB=
AB=![]() ,AF=1,M是线段EF的中点。
,AF=1,M是线段EF的中点。
(Ⅰ)求证:AM∥平面BDE;
(Ⅱ) 求二面角A-DF-B的大小.
(Ⅲ)试问:在线段AC上是否存在一点P,使得直线PF与AD所成角为60°?
22.(本题满分14分)已知=(c,0)(c>0), =(n,n)(n∈R), 的最小值为1,若动点P同时满足下列三个条件:
① = (a>c>0);
② =![]() (其中=(,t),
(其中=(,t),![]() ≠0,t∈R);
≠0,t∈R);
③动点P的轨迹C经过点B(0,-1) .
(Ⅰ)求c的值;
(Ⅱ)求曲线C的方程;
(Ⅲ)是否存在方向向量为a=(1,k)(k≠0)的直线l,使l与曲线C交于两个不同的点M、N,且=?若存在,求出k的范围;若不存在,请说明理由.
23.(本题满分14分)
|
(Ⅰ)试求数列{![]() }的通项公式
}的通项公式![]() ;(用
;(用![]() 的代数式表示)
的代数式表示)
(Ⅱ)求证:![]()
(Ⅲ)求证:![]() (注:
(注:![]() ).
).
08年咸阳市高考数学第一次模拟考试
参考答案及评分标准
一、选择题
1.C 易知A={-1,0,1},B={1,2},故A∩B={1}.
2.D 分x<1与2≤x<5讨论.
3.D =+λ(+)=+2λ(其中D为BC的中点),于是有=2λ,从而点A、D、P共线,即点P的轨迹通过三角形ABC的重心.
4.B 作出不等式表示的平面区域即可.
5.A 先从14人中选出12人,再将12人进行分组,且每组4人.
6.B 由线面位置关系不难知道:①③正确的.
7.B [解析]由题意知:等差数列中,从第1项到第2005项是正数,且从第2006项开始为负数,S4010=2005(a1+a4010)=2005(a2005+a2006)>0,
S4011==4011a2006<0, 故n的最大值为4010.
另解:由题意可得:等差数列中,从第1项到第2005项是正数,且从第2006项开始是负数,则所有的正项的和为Sn的最大值,即当n=2005时,取得最大值,显然Sn是关于n的缺常数项的二次函数,且开口向下,所以第2005项离对称轴最近,故其对称轴介于2005到2005.5之间,又因为二次函数的图象与x轴的一个交点是(0,0),则设另一个交点(x,0),x应介于4010到4011之间.所以使Sn>0的最大自然数是4010,故选B.
本小题结论可以推广成一般结论:等差数列中,a1>0,ak+ak+1>0,且akak+1<0,则使前n项和Sn>0的最大自然数n是2k..
8.B 原函数的图象是由y=图象向下移动一个单位,且在(-∞,0),(0,+∞)上为减函数,所以其反函数的图象是由y=的图象向左移动一个单位,且在定义域上为减函数.
9.B 易知面BCC1B1内的点到点F的距离是到BC的距离倍的,由椭圆的第二定义即知.
10.D 设 M F双曲线的交点为P,焦点F(-c,0), F2(c,0),由平面几何知识知:F2P⊥FM,又F F2=2c 于是 PF2 =2csin60°=c PF1 =c
故 2a= PF2 -PF1 =c-c =( -1)c e= =+1.
11.C
特值法:令a=2与可知![]() 在
在![]() 上恒正,显然选项D不正确.
上恒正,显然选项D不正确.
12.B 依题意知PMQ曲线是以A、B为焦点、实轴长为2的双曲线的一支(以B为焦点),此双曲线的离心率为2,以直线AB为轴、AB的中点为原点建立平面直角坐标系,则该双曲线的方程为 x2-=1,点C的坐标为(3,).则修建这条公路的总费用ω=a[MB+2MC]=2a[MB+MC],设点M、C在右准线上射影分别为点M 、C ,根据双曲线的定义有M M=MB,所以=2a[M M+MC]≥2aC C=2a×(3-)=5a.当且仅当点M在线段C C上时取等号,故ω的最小值是5a.
二、填空题
13.200 易知A=2 ,ω= ,![]() =±,y=2-cos(πx+)=2±sinπx,从而
=±,y=2-cos(πx+)=2±sinπx,从而
f(1)+f(2)+f(3)+…+f(100)=2×100=200.
14.![]() [解析]∵y’=3x2-
[解析]∵y’=3x2-![]() ≥-
≥-![]() , ∴tanα≥-
, ∴tanα≥-![]()
又∵ 0≤α≤∏
∴0≤α<![]()
15. ![]() 由二项式定理知:
由二项式定理知: ![]() 的展开式中
的展开式中![]() 的系数为 C·
的系数为 C·![]() ,
,![]() 的展开式中
的展开式中![]() 的系数为C·,于是有C·
的系数为C·,于是有C·![]() = C·,解得
= C·,解得 ![]() =.
=.
16.①、③ 可通过作差比较得到结论.
17. 283 [解析] 由条件知道:该数列的奇数项分别为1,3,6,10,15,21,28,36,45,55,…,偶数项分别为3,4,5,6,7,8,9,10,11,…,把奇数项的前10项与偶数项的前9项相加即得S19=283.
18. 4012 [解析]∵f(1+0)=f(1)·f(0),2=2f(0),∴f(0)=1
∵f(2)=f(1+1)=f(1)·f(1)=22,
f(3)=f(2+1)=f(2)·f(1)=23,
依此类推:f(2005)=22005,f(2006)=22006,
∴原式=![]() =4012.
=4012.
三、解答题
19.解:(Ⅰ) ![]() 1分
1分
![]() =
=
![]() =
=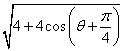 =
=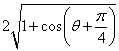 3分
3分
∵θ∈[π,2π],∴![]() ,∴
,∴![]() ≤1
≤1
![]() max=2
max=2![]() .
5分
.
5分
(Ⅱ) 由已知![]() ,得
,得![]() 7分
7分
又![]() ∴
∴![]() 10分
10分
∵θ∈[π,2π]∴![]() ,∴
,∴![]() .
12分
.
12分
20.解: (Ⅰ) 比赛以甲3胜1而结束,则第四局一定甲胜,前三局中甲胜两局, 1分
∴所求概率为:![]() .
3分
.
3分
答:比赛以甲3胜1而结束的概率为![]() .
4分
.
4分
(Ⅱ) 比赛以乙3胜2而结束,则第五局一定乙胜,前四局中乙胜两局, 5分
∴所求概率为: ![]() 7分
7分
答:比赛以乙3胜2而结束的概率为![]() .
8分
.
8分
(Ⅲ)甲先胜3局的情况有3种:3胜无败,3胜1败,3胜2败.,则其概率分别为 9分
![]() ,
,![]() =
=![]() ,
,![]() ,
,
于是甲获胜的概率![]() 11分
11分
 ∴乙获胜的概率
∴乙获胜的概率![]() ∴
∴![]() .
.![]() 12分
12分
21.方法一
解: (Ⅰ)记AC与BD的交点为O,连接OE, 1分
∵O、M分别是AC、EF的中点,ACEF是矩形,
∴四边形AOEM是平行四边形, 2分
∴AM∥OE. 3分
∵![]() 平面BDE,
平面BDE, ![]() 平面BDE,
平面BDE,
∴AM∥平面BDE. 4分
(Ⅱ)在平面AFD中过A作AS⊥DF于S,连结BS,
∵AB⊥AF, AB⊥AD, ![]()
∴AB⊥平面ADF, 5分
∴AS是BS在平面ADF上的射影,
由三垂线定理得BS⊥DF.
∴∠BSA是二面角A—DF—B的平面角。 7分
在RtΔASB中,![]()
∴![]() 8分
8分
∴二面角A—DF—B的大小为60º. 9分
(Ⅲ)设CP=t(0≤t≤2),作PQ⊥AB于Q,则PQ∥AD,
∵PQ⊥AB,PQ⊥AF,![]() ,
,
∴PQ⊥平面ABF,QF![]() 平面ABF,
平面ABF,
∴PQ⊥QF. 11分
在RtΔPQF中,∠FPQ=60º,PF=2PQ.
∵ΔPAQ为等腰直角三角形,
∴![]() 12分
12分
又∵ΔPAF为直角三角形,
∴![]() ,
,
∴![]()
所以t=1或t=3(舍去)
即点P是AC的中点. 14分
方法二( 仿上给分)
(Ⅰ)建立如图所示的空间直角坐标系。
设![]() ,连接NE,
,连接NE,
则点N、E的坐标分别是(![]() 、(0,0,1),
、(0,0,1),
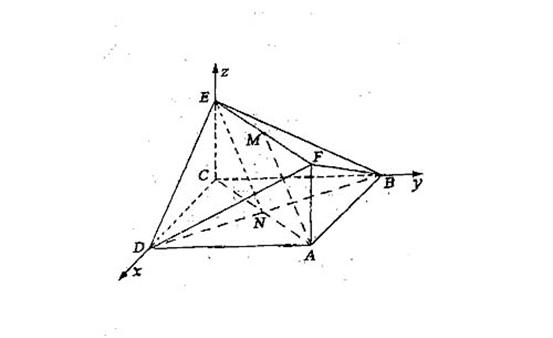
![]() ∴NE=(
∴NE=(![]() ,
,
又点A、M的坐标分别是
(![]() )、(
)、(![]()
![]() ∴ AM=(
∴ AM=(![]()
![]()
![]() ∴NE=AM且NE与AM不共线,
∴NE=AM且NE与AM不共线,
∴NE∥AM.
又∵![]() 平面BDE,
平面BDE, ![]() 平面BDE,
平面BDE,
∴AM∥平面BDF.
(Ⅱ)∵AF⊥AB,AB⊥AD,AF![]()
∴AB⊥平面ADF.
![]() ∴
∴ ![]() 为平面DAF的法向量。
为平面DAF的法向量。
![]()
![]() ∵NE·DB=(
∵NE·DB=(![]() ·
·![]() =0,
=0,
![]()
![]() ∴NE·NF=(
∴NE·NF=(![]() ·
·![]() =0得
=0得
![]()
![]()
![]()
![]() NE⊥DB,NE⊥NF,
NE⊥DB,NE⊥NF,
![]() ∴NE为平面BDF的法向量。
∴NE为平面BDF的法向量。
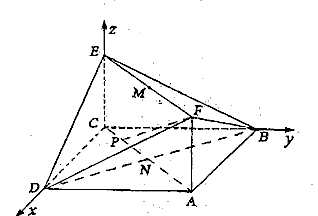
![]()
![]() ∴cos<AB,NE>=
∴cos<AB,NE>=![]()
![]()
![]() ∴AB与NE的夹角是60º.
∴AB与NE的夹角是60º.
即所求二面角A—DF—B的大小是60º.
(Ⅲ)设P(t,t,0)(0≤t≤![]() )得
)得
![]()
![]()
![]() ∴DA=(0,
∴DA=(0,![]() ,0,),
,0,),
又∵PF和AD所成的角是60º.
∴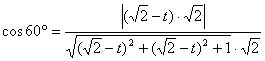
解得![]() 或
或![]() (舍去),
(舍去),
即点P是AC的中点.
22.解:(Ⅰ)法一: == ,
当n= 时, min==1,所以c=. 3分
法二:设G(x,y),则G在直线y=x上,所以的最小值为点F到直线y=x的距离,即
=1,得c=.
(Ⅱ)∵=![]() (
(![]() ≠0),∴PE⊥直线x= , 又 = (a>c>0).
≠0),∴PE⊥直线x= , 又 = (a>c>0).
∴点P在以F为焦点,x= 为准线的椭圆上. 5分
设P(x,y), 则有 = -x, 点B(0-1)代入, 解得a=.
∴曲线C的方程为 +y2=1 7分
(Ⅲ)假设存在方向向量为a0=(1,k)(k≠0)的直线l满足条件,则可设l:y=kx+m(k≠0),
与椭圆+y2=1联立,消去y得(1+3k2)x2+6kmx+3m2-3=0. 10分
由判别式△>0,可得m2<3k2+1. ①
设M(x1,y1),N(x2,y2), MN的中点P(x0,y0),由BM=BN, 则有BP⊥MN.
由韦达定理代入kBP=-,可得到m= ②
联立①②,可得到 k2-1<0, 12分
∵k≠0, ∴ -1<k<0或0<k1.
即存在k∈(-1,0)∪(0,1),使l与曲线C交于两个不同的点M、N,且=. 14分
23.解: (Ⅰ) ![]()
![]() ,若切点是
,若切点是![]() ,则
,则
切线方程为![]() .
1分
.
1分
当n=1时,切线过点(1,0),即![]() ,得
,得![]()
当n>1时,切线过点![]() ,即
,即![]() ,解得
,解得![]() .
.
![]() 数列
数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
故所求通项![]() .
4分
.
4分
(Ⅱ) 由(1)知![]()
![]()
![]()
![]() 9分
9分
(Ⅲ)设![]() ,则
,则![]() ,
,
两式相减得![]() ,
,
![]()
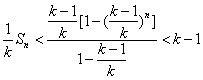 . 故
. 故![]() .
14分
.
14分