专题四 高考数学三角函数复习训练
高考试题中的三角函数题相对比较传统,位置靠前,通常以简单题形式出现。因此,在复习过程中要特别注重三角知识的基础性,突出三角函数的图象及其变换、周期性、单调性、奇偶性、对称性等性质,以及化简、求值和最值等重点内容的复习,要求考生熟练记忆和应用三角公式及其恒等变形,同时要注重三角知识的工具性.近年来,三角函数与向量联系问题有所增加,三角知识在几何及实际问题中的应用也是考查重点,应给于充分的重视。
一、知识整合
1.熟练掌握三角变换的所有公式,理解每个公式的意义,应用特点,常规使用方法等;熟悉三角变换常用的方法——化弦法,降幂法,角的变换法等;并能应用这些方法进行三角函数式的求值、化简、证明;掌握三角变换公式在三角形中应用的特点,并能结合三角形的公式解决一些实际问题.
2.熟练掌握正弦函数、余弦函数、正切函数、余切函数的性质,并能用它研究复合函数的性质;熟练掌握正弦函数、余弦函数、正切函数、余切函数图象的形状、特点,并会用五点画出函数![]() 的图象;理解图象平移变换、伸缩变换的意义,并会用这两种变换研究函数图象的变化.
的图象;理解图象平移变换、伸缩变换的意义,并会用这两种变换研究函数图象的变化.
3.注重三角函数与代数、向量、几何及实际问题中的应用,能利用三角函数相关知识解决综合问题.
二、典型例题分析
例1.扇形![]() 的中心角为
的中心角为![]() ,半径为
,半径为![]() ,在扇形
,在扇形![]() 中作内切圆
中作内切圆![]() 及与圆
及与圆![]() 外切,与
外切,与![]() 相切的圆
相切的圆![]() ,问
,问![]() 为何值时,圆
为何值时,圆![]() 的面积最大?最大值是多少?
的面积最大?最大值是多少?
解:设圆![]() 及与圆
及与圆![]() 的半径分别为
的半径分别为![]() ,
,
则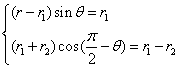 ,得
,得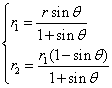 ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,令
,令![]() ,
,
![]() ,当
,当![]() ,即
,即![]() 时,
时,
圆![]() 的半径最大,圆
的半径最大,圆![]() 的面积最大,最大面积为
的面积最大,最大面积为![]() .
.
例2、(05天津)已知![]() ,求
,求![]() 及
及![]() .
.
【解析】解法一:由题设条件,应用两角差的正弦公式得
![]() ,即
,即![]() ①
①
由题设条件,应用二倍角余弦公式得
![]()
故![]() ②
②
由①和②式得![]() ,
,![]()
![]()
因此,![]() ,由两角和的正切公式
,由两角和的正切公式
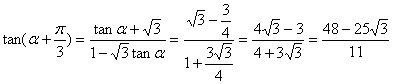
解法二:由题设条件,应用二倍角余弦公式得![]() ,
,
解得 ![]() ,即
,即![]()
![]()
由![]() 可得
可得![]()
![]()
由于![]() ,且
,且![]() ,故a在第二象限
,故a在第二象限![]() 于是
于是![]() ,
,
从而![]()
![]()
以下同解法一![]()
【点评】1、本题以三角函数的求值问题考查三角变换能力和运算能力,可从已知角和所求角的内在联系(均含![]() )进行转换得到.
)进行转换得到.
2、在求三角函数值时,必须灵活应用公式,注意隐含条件的使用,以防出现多解或漏解的情形.
例3:设0<θ<![]() ,曲线x2sinθ+y2cosθ=1和x2cosθ-y2sinθ=1有4个不同的交点.
,曲线x2sinθ+y2cosθ=1和x2cosθ-y2sinθ=1有4个不同的交点.
(1)求θ的取值范围;
(2)证明这4个交点共圆,并求圆半径的取值范围.
解:(1)解方程组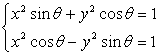 ,得
,得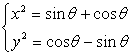
故两条已知曲线有四个不同的交点的充要条件为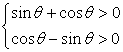 ,(0<θ<
,(0<θ<![]() )
)![]() 0<θ<
0<θ<![]() .
.
(2)设四个交点的坐标为(xi,yi)(i=1,2,3,4),
则:xi2+yi2=2cosθ∈(![]() ,2)(i=1,2,3,4).
,2)(i=1,2,3,4).
故四个交点共圆,并且这个圆的半径r=![]() cosθ∈(
cosθ∈(![]() ).
).
评注:本题注重考查应用解方程组法处理曲线交点问题,这也是曲线与方程的基本方法,同时本题也突出了对三角不等关系的考查.
例4:设关于x的方程sinx+![]() cosx+a=0在(0, 2π)内有相异二解α、β.
cosx+a=0在(0, 2π)内有相异二解α、β.
(Ⅰ)求α的取值范围; (Ⅱ)求tan(α+β)的值.
解: (Ⅰ)∵sinx+![]() cosx=2(
cosx=2(![]() sinx+
sinx+![]() cosx)=2 sin(x+
cosx)=2 sin(x+![]() ),
),
∴方程化为sin(x+![]() )=-
)=-![]() .
.
∵方程sinx+![]() cosx+a=0在(0, 2π)内有相异二解,
cosx+a=0在(0, 2π)内有相异二解,
∴sin(x+![]() )≠sin
)≠sin![]() =
=![]() .
.
又sin(x+![]() )≠±1 (∵当等于
)≠±1 (∵当等于![]() 和±1时仅有一解),
和±1时仅有一解),
∴-![]() <1 . 且-
<1 . 且-![]() ≠
≠![]() . 即a<2
. 即a<2
且a≠-![]() . ∴ a的取值范围是(-2, -
. ∴ a的取值范围是(-2, -![]() )∪(-
)∪(-![]() , 2).
, 2).
(Ⅱ) ∵α、 β是方程的相异解, ∴sinα+![]() cosα+a=0
①.
cosα+a=0
①.
sinβ+![]() cosβ+a=0 ②.
cosβ+a=0 ②.
①-②得(sinα- sinβ)+![]() ( cosα- cosβ)=0.
( cosα- cosβ)=0.
∴ 2sin![]() cos
cos![]() -2
-2![]() sin
sin![]()
sin![]() =0, 又sin
=0, 又sin![]() ≠0, ∴tan
≠0, ∴tan![]() =
=![]() .
.
∴tan(α+β)=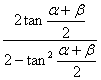 =
=![]() .
.
【点评】要注意三角函数实根个数与普通方程的区别,这里不能忘记(0, 2π)这一条件.
例5 已知函数![]() 的最小正周期为
的最小正周期为![]() ,其图像过点
,其图像过点![]() .
.
(Ⅰ) 求![]() 和
和![]() 的值;(Ⅱ) 函数
的值;(Ⅱ) 函数![]() 的图像可由
的图像可由![]() (x∈R)的图像经过怎样的变换而得到?
(x∈R)的图像经过怎样的变换而得到?
解: (Ⅰ) ![]() 函数
函数![]() 的最小正周期为
的最小正周期为![]() ,
, ![]()
![]() .
.
![]() .
. ![]() .
.
![]() 的图像过点
的图像过点![]() ,
, ![]() , 即
, 即![]() .
.
![]() ,
,
![]() .
.
(Ⅱ)先把![]() 的图像上所有点向左平移
的图像上所有点向左平移![]() 个单位(纵坐标不变),得到函数
个单位(纵坐标不变),得到函数![]() 的图像,
的图像,
再把所得的函数图像上所有点的纵坐标伸长为原来的2倍(横坐标不变)得到函数![]() 的图像.
的图像.
【点评】三角函数图像及其变换是当前考查热点,其书写的规范性是考生必须高度重视的.
例6、(2007年湖南卷文16)
已知函数![]() .求:
.求:
(I)函数![]() 的最小正周期;
的最小正周期;
(II)函数![]() 的单调增区间.
的单调增区间.
解:![]()
![]() .
.
(I)函数![]() 的最小正周期是
的最小正周期是![]() ;
;
(II)当![]() ,即
,即![]() (
(![]() )时,函数
)时,函数![]() 是增函数,故函数
是增函数,故函数![]() 的单调递增区间是
的单调递增区间是![]() (
(![]() ).
).
【点评】本题主要考查三角函数的基本公式、三角恒等变换、三角函数的性质以及推理和运算能力.
例7 、已知:![]()
(1)请说明函数![]() 的图象可由函数
的图象可由函数![]() 的图象经过怎样的变换得到;
的图象经过怎样的变换得到;
(2)设函数![]() 图象位于y轴右侧的对称中心从左到右依次为A1、A2、A3、A4、…、
图象位于y轴右侧的对称中心从左到右依次为A1、A2、A3、A4、…、![]() …、
…、![]() ,试求A4的坐标。
,试求A4的坐标。
解:(1)![]()
![]()
![]()
∴![]()
![]()
![]()
![]()
所以函数![]() 的图象可由函数
的图象可由函数![]() 的图象向左平移
的图象向左平移![]() 个单位得到
个单位得到
(2)∵函数![]() 图象的对称中心为
图象的对称中心为![]() ,
,![]()
由![]() 得函数
得函数![]() 的对称中心为
的对称中心为![]() ,
,
![]() 依次取1,2,3,4……可得A1、A2、A3、A4……各点,
依次取1,2,3,4……可得A1、A2、A3、A4……各点,
∴A4的坐标为![]()
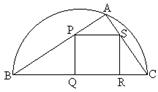
例8、如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余的地方种花.若BC=a,∠ABC=![]() ,设△ABC的面积为S1,正方形的面积为S2.
,设△ABC的面积为S1,正方形的面积为S2.
|
(2)当a固定,![]() 变化时,求
变化时,求![]() 取最小值时的角
取最小值时的角![]()
解(1)∵![]()
∴![]()
设正方形边长为x.
则BQ=![]()
![]()
![]()
![]()
(2)当![]() 固定,
固定,![]() 变化时,
变化时,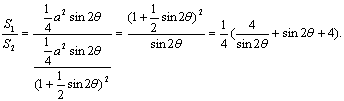
令![]()
![]() 令
令![]() 任取
任取![]() ,且
,且![]() ,
,
![]() .
.
![]() ,
,
![]() 是减函数.
是减函数.![]() 取最小值,此时
取最小值,此时![]()
三、方法总结与2008年高考预测
1.三角函数恒等变形的基本策略。
(1)常值代换:特别是用“1”的代换,如1=cos2x+sin2x=tanx·cotx=tan45°等。
(2)项的分拆与角的配凑。如分拆项:sin2x+2cos2x=(sin2x+cos2x)+cos2x=1+cos2x;
配凑角:α=(α+β)-β,β=![]() -
-![]() 等。
等。
(3)升幂与降幂。
(4)化弦(切)法。
(5)引入辅助角。asinθ+bcosθ=![]() sin(θ+
sin(θ+![]() ),这里辅助角
),这里辅助角![]() 所在象限由a、b的符号确定,
所在象限由a、b的符号确定,![]() 角的值由tan
角的值由tan![]() =
=![]() 确定。
确定。
2.证明三角等式的思路和方法。
(1)思路:利用三角公式进行化名,化角,改变运算结构,使等式两边化为同一形式。
(2)证明方法:综合法、分析法、比较法、代换法、相消法、数学归纳法。
3.证明三角不等式的方法:比较法、配方法、反证法、分析法,利用函数的单调性,利用正、余弦函数的有界性,利用单位圆三角函数线及判别法等。
4.解答三角高考题的策略。
(1)发现差异:观察角、函数运算间的差异,即进行所谓的“差异分析”。
(2)寻找联系:运用相关公式,找出差异之间的内在联系。
(3)合理转化:选择恰当的公式,促使差异的转化。
5.高考考点分析
2005-207年各地高考中本部分所占分值在14~20分,主要以选择题和解答题的形式出现。主要考察内容按综合难度分,我认为有以下几个层次:
第一层次:通过诱导公式和倍角公式的简单运用,解决有关三角函数基本性质的问题。如判断符号、求值、求周期、判断奇偶性等。
第二层次:三角函数公式变形中的某些常用技巧的运用。如辅助角公式、平方公式逆用、切弦互化等。
第三层次:充分利用三角函数作为一种特殊函数的图象及周期性、奇偶性、单调性、有界性等特殊性质,解决较复杂的函数问题。如分段函数值,求复合函数值域等。
四.强化训练
一、选择题:
1.(2007年全国高考题)函数f (x) = sin x+cos x 的最小正周期是 ( )
A. B. C.π D.2π
2.若![]() 的终边所在象限是 (
)
的终边所在象限是 (
)
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知函数![]() ,则下列判断正确的是( )
,则下列判断正确的是( )
(A)此函数的最小正周期为![]() ,其图象的一个对称中心是
,其图象的一个对称中心是![]()
(B)此函数的最小正周期为![]() ,其图象的一个对称中心是
,其图象的一个对称中心是![]()
(C)此函数的最小正周期为![]() ,其图象的一个对称中心是
,其图象的一个对称中心是![]()
(D)此函数的最小正周期为![]() ,其图象的一个对称中心是
,其图象的一个对称中心是![]()
4.在△OAB中,O为坐标原点,![]() ,则当△OAB的面积达最大值时,
,则当△OAB的面积达最大值时,![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
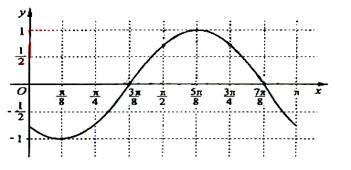
5.函数![]() 的部分图像如图所示,则函数表达式为
的部分图像如图所示,则函数表达式为
( )
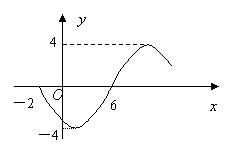 (A)
(A)![]()
(B)![]()
(C)![]()
(D)![]()
6.设![]() 是某港口水的深度y(米)关于时间t(时)的函数,其中
是某港口水的深度y(米)关于时间t(时)的函数,其中![]() .下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
经长期观观察,函数![]() 的图象可以近似地看成函数
的图象可以近似地看成函数![]() 的图象.在下面的函数中,最能近似表示表中数据间对应关系的函数是 ( )
的图象.在下面的函数中,最能近似表示表中数据间对应关系的函数是 ( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
7.将函数![]() 的图象先向左平移
的图象先向左平移![]() ,然后将所得图象上所有点的横坐标变为原来的
,然后将所得图象上所有点的横坐标变为原来的![]() 倍(纵坐标不变),则所得到的图象对应的函数解析式为( ).
倍(纵坐标不变),则所得到的图象对应的函数解析式为( ).
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
8.已知k<-4,则函数y=cos2x+k(cosx-1)的最小值是( )
(A) 1 (B) -1 (C) 2k+1 (D) -2k+1
9.使![]() (ω>0)在区间[0,1]至少出现2次最大值,则ω的最小值为( )
(ω>0)在区间[0,1]至少出现2次最大值,则ω的最小值为( )
A.![]() B.
B.![]() C.π D.
C.π D.![]()
10. 在△ABC中,sinA=![]() ,cosB=
,cosB=![]() ,则cosC等于
( )
,则cosC等于
( )
A.![]() B.
B.![]() C.
C. ![]() 或
或![]() D.
D.![]()
11.当![]() 时,函数
时,函数![]() 的最小值为 (
)
的最小值为 (
)
(A)2 (B)![]() (C)4 (D)
(C)4 (D)![]()
12.在△OAB中,O为坐标原点,![]() ,则当△OAB的面积达最大值时,
,则当△OAB的面积达最大值时,![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:
13.若![]() -
-![]() ,
,![]() ∈(0,π),则tan
∈(0,π),则tan![]() =
。
=
。
14.![]() ,则
,则![]() 范围
。
范围
。
15.下列命题正确的有_________。
①若-![]() <
<![]() <
<![]() <
<![]() ,则
,则![]() 范围为(-π,π);
范围为(-π,π);
②若![]() 在第一象限,则
在第一象限,则![]() 在一、三象限;
在一、三象限;
③若![]() =
=![]() ,
,![]() ,则m∈(3,9);
,则m∈(3,9);
④![]() =
=![]() ,
,![]() =
=![]() ,则
,则![]() 在一象限。
在一象限。
16.如图,一个半径为10米的水轮按逆时针方向每分钟转4圈.记水轮上的点P到水面的距离为d米(P在水面下则d为负数),则d(米)与时间t(秒)之间满足关系式:![]() ,且当P点从水面上浮现时开始计算时间.有以下四个结论:①A=10;②
,且当P点从水面上浮现时开始计算时间.有以下四个结论:①A=10;②![]() ;③
;③![]() ; ④k=5. 则其中所有正确结论的序号是
.
; ④k=5. 则其中所有正确结论的序号是
.
三、解答题:
17. 化简: ![]() .
.
18.已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
19.设函数![]() 图像的一条对称轴是直线
图像的一条对称轴是直线![]() 。
。
(Ⅰ)求![]() ;(Ⅱ)求函数
;(Ⅱ)求函数![]() 的单调增区间;
的单调增区间;
(Ⅲ)画出函数![]() 在区间
在区间![]() 上的图像。
上的图像。
20.一条直角走廊宽1.5米,如图所示.现有一转动灵活的手推车,其平板面的矩形宽为1米,问要想顺利推过直角走廊,平板车的长度不能超过多少米?
21. 在 △ABC 中,已知角 A 为锐角,且
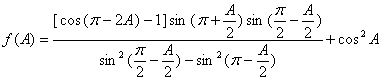 .
.
(Ⅰ)求 ![]() 的最大值;
的最大值;
(Ⅱ)若 ![]() ,
,![]() ,
,![]() ,求 △ABC 的三个内角和 AC 边的长.
,求 △ABC 的三个内角和 AC 边的长.
22. 设函数![]() .
.
(Ⅰ)求函数![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(Ⅱ)当![]() 时,
时,![]() 的最大值为2,求
的最大值为2,求![]() 的值,并求出
的值,并求出![]() 的对称轴方程.
的对称轴方程.
23.设函数![]() 的图象过点P(0,1),且
的图象过点P(0,1),且![]() 的最大值是2,最小值为-2,其中
的最大值是2,最小值为-2,其中![]() .
.
(1)求![]() 表达式;
表达式;
(2)若射线![]() 图象交点的横坐标,由小到大依次为
图象交点的横坐标,由小到大依次为![]() 求
求![]() 的值.
的值.
(四)、创新试题
例9、已知奇函数f(x)的定义域为实数集,且f(x)在![]() 上是增函数,当
上是增函数,当![]() 时,是否存在这样的实数m,使
时,是否存在这样的实数m,使![]() 对所有的
对所有的![]() 均成立?若存在,求出所有适合条件的实数m;若不存在,说明理由。
均成立?若存在,求出所有适合条件的实数m;若不存在,说明理由。
解:![]() 为奇函数,
为奇函数,![]()
![]()
![]()
又![]() 在
在![]() 上是增函数,且
上是增函数,且![]() 是奇函数
是奇函数 ![]() 是R上的增函数,
是R上的增函数,
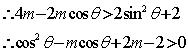
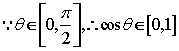 ,令
,令![]()
![]() 满足条件的
满足条件的![]() 应该使不等式
应该使不等式![]() 对任意
对任意![]() 均成立。
均成立。
设![]() ,由条件得
,由条件得
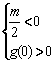 或
或 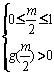 或
或 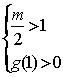 解得,
解得,![]() 或
或![]()
即![]() 存在,取值范围是
存在,取值范围是![]()
例10、已知函数![]() 其中
其中![]() 为参数,且
为参数,且![]()
(1)当![]() 时,判断函数
时,判断函数![]() 是否有极值;
是否有极值;
(2)要使函数![]() 的极小值大于零,求参数
的极小值大于零,求参数![]() 的取值范围;
的取值范围;
(3)若对(2)中所求的取值范围内的任意参数![]() ,函数
,函数![]() 在区间
在区间![]() 内都是增函数,求实数
内都是增函数,求实数![]() 的取值范围。
的取值范围。
解:(1)当![]() 时
时![]() 则
则![]() 在
在![]() 内是增函数,故无极值。
内是增函数,故无极值。
(2)![]() 令
令![]() 得
得 ![]()
由![]() 及(I),只需考虑
及(I),只需考虑![]() 的情况。
的情况。
当![]() 变化时,
变化时,![]() 的符号及
的符号及![]() 的变化情况如下表:
的变化情况如下表:
|
|
| 0 |
|
|
|
|
| + | 0 | - | 0 | + |
|
| 递增 | 极大值 | 递减 | 极小值 | 递增 |
因此,函数![]() 在
在![]() 处取得极小值
处取得极小值![]() 且
且![]()
要使![]() 必有
必有![]() 可得
可得![]() 所以
所以![]()
(3)由(2)知,函数![]() 在区间
在区间![]() 与
与![]() 内都是增函数。
内都是增函数。
由题设,函数![]() 在
在![]() 内是增函数,则
内是增函数,则![]() 须满足不等式组
须满足不等式组
![]() 或
或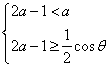
由(II),参数![]() 时,
时,![]() 要使不等式
要使不等式![]() 关于参数
关于参数![]() 恒成立,必有
恒成立,必有![]() 综上,解得
综上,解得![]() 或
或![]() 所以
所以![]() 的取值范围是
的取值范围是![]()
参考答案:
一.选择题:
1.C. 2.D. 3.B 4.D. 5.A 6.A. 7.D. 8.A 9. A 10.A 11。D 12.D
9. [解析]:要使![]() (ω>0)在区间[0,1]至少出现2次最大值
(ω>0)在区间[0,1]至少出现2次最大值
只需要最小正周期![]()
![]()
![]() 1,故
1,故![]()
![]() 10.
10.![]() [解析]:∵ cosB=
[解析]:∵ cosB=![]() ,∴B是钝角,∴C就是锐角,即cosC>0,故选A
,∴B是钝角,∴C就是锐角,即cosC>0,故选A
二.填空题:
13.![]() 或
或![]()
[解析]: ∵![]() -
-![]() >1,且
>1,且![]() ∈(0,π)∴
∈(0,π)∴![]() ∈(
∈(![]() ,π)
,π)
∴ (![]() -
-![]() ∴2sin
∴2sin![]() cos
cos![]() =
=![]()
∴![]() +
+![]()
∴sin![]() =
=![]() cos
cos![]() =
=![]() 或sin
或sin![]() =
=![]() cos
cos![]() =
=![]()
tan![]() =
=![]() 或
或![]()
14.![]()
[解析]: ∵![]()
![]() =
=![]()
∴![]()
![]() =
=![]()
∴![]()
![]()
又![]()
![]() =
=![]()
∴![]()
![]() =
=![]()
∴![]()
![]()
故![]()
15.②④
[解析]:∵若-![]() <
<![]() <
<![]() <
<![]() ,则
,则![]() 范围为(-π,0)∴①错
范围为(-π,0)∴①错
∵若![]() =
=![]() ,
,![]() ,则m∈(3,9)
,则m∈(3,9)
又由![]() 得m=0或 m=8
得m=0或 m=8
∴m=8
故③错
16.①②④.
三、解答题:
17.解: 原式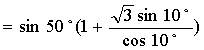
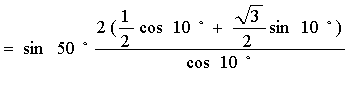
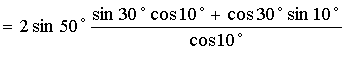
![]() =
=![]() =
=![]() =1
=1
18.解:由题设知![]() 为第一象限角
为第一象限角
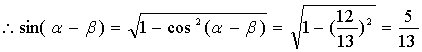
由题设知![]() 为第三象限角
为第三象限角
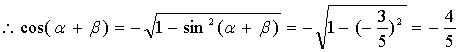
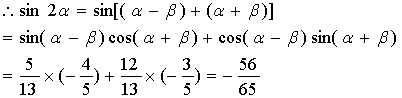
19.(Ⅰ)解:![]() .
.
因此,函数![]() 的最小正周期为
的最小正周期为![]() .
.
(Ⅱ)解法一:因为![]() 在区间
在区间![]() 上为增函数,在区间
上为增函数,在区间![]() 上为减函数,又
上为减函数,又![]() ,
,![]() ,
,![]() ,
,
故函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() .
.
解法二:作函数![]() 在长度为一个周期的区间
在长度为一个周期的区间![]() 上的图象如下:
上的图象如下:
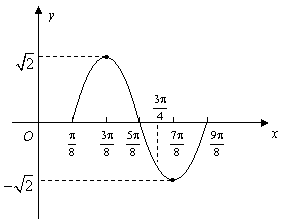
由图象得函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() .
.
20.本小题主要考查三角函数性质及图像的基本知识,考查推理和运算能力,满分12分.
解:(Ⅰ)![]() 的图像的对称轴,
的图像的对称轴,![]()
![]()
![]()
(Ⅱ)由(Ⅰ)知![]()
由题意得 ![]()
所以函数![]()
(Ⅲ)由![]()
| x | 0 |
|
|
|
|
|
| y |
| -1 | 0 | 1 | 0 |
|
|
20 . 解:如图,延长AB交直角走廊于A1、B1,设∠CDE1=,则∠B1A1E1=,∈(0,).
∵ CD=AB=A1B1-AA1-BB1,
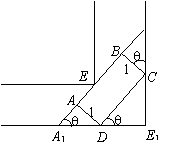 而 A1B1=1.5(+),AA1=cot,BB1=tan,
而 A1B1=1.5(+),AA1=cot,BB1=tan,
∴ CD=1.5(+)―cot―tan
=.
令sin+cos=t,则t∈(1,].
令 f(t)== ,
显然,函数f(t)在(1,]上是减函数,所以当t=,即=时,
CDmin=f(t)min=3-2.
故平板车的长度不能超过3-2米.
19.解:(Ⅰ)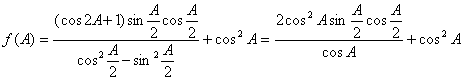
![]() .
.
∵ 角 A 为锐角,∴ ![]() ,
,![]() .
.
∴ 当 ![]() 时,
时,![]() 取得最大值,其最大值为
取得最大值,其最大值为![]() .
.
(Ⅱ)由![]() 得
得 ![]() ,∴
,∴![]() .
.
∴ ![]() ,
,![]() .又 ∵
.又 ∵![]() ,∴
,∴ ![]() .∴
.∴ ![]() .
.
在 △ABC 中,由正弦定理得:![]() .∴
.∴ ![]() .
.
21.解:(1)![]()
则![]() 的最小正周期
的最小正周期![]() ,
,
且当![]() 时
时![]() 单调递增.
单调递增.
即![]() 为
为![]() 的单调递增区间(写成开区间不扣分).
的单调递增区间(写成开区间不扣分).
(2)当![]() 时
时![]() ,当
,当![]() ,即
,即![]() 时
时![]() .
.
所以![]() .
.
![]() 为
为![]() 的对称轴.
的对称轴.
22. (1)![]()
![]()
![]()
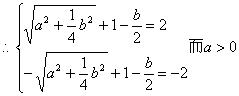
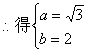
![]()
(2)由题意,知![]()
即![]()
![]()
![]() 的等差数列
的等差数列
![]()
![]()
![]()
23.已知函数![]() 的图象上以N(1,n)为切点的切线倾斜角为
的图象上以N(1,n)为切点的切线倾斜角为![]() .
.
(1)求m,n的值;
(2)是否存在最小的正整数k,使得不等式![]() 恒成立?若存在,求出最小的正整数k,否则请说明理由.
恒成立?若存在,求出最小的正整数k,否则请说明理由.
(3)求出![]() 的取值范围.
的取值范围.
22.(1)![]()
![]()
![]()
从而由![]()
![]() ……………………4分
……………………4分
(2)![]()
令![]() …………………………5分
…………………………5分
在[-1,3]中,当![]() 为增函数,
为增函数,
当![]() 为减函数
为减函数
![]() 时取得极大值
时取得极大值
当![]() 为增函数时f(3) 为
为增函数时f(3) 为![]() 的极大值………………8分
的极大值………………8分
比较![]() ………………9分
………………9分
![]()
![]() ……………………10分
……………………10分
(3)![]()
![]()
![]()
=![]()
=![]()
=![]()
![]() …………………………14分
…………………………14分
五、复习的建议
立足课本,抓好基础。注意三角函数作为函数的特征的运用。如在解决周期性、奇偶性、最值等问题时有关数学思想的运用。
1, 加强对三角函数图象的研究。使学生熟练地求解有关图象的特征、图象的对称性、变换、解析式、五点作图等问题。
2, 熟练掌握三角变换的基本公式,弄清公式的推导关系和互相联系,把基本公式记准用熟。在三角变换中经常出现公式的逆用或变形,尤其是二倍角余弦公式、两角和差的正切的变形应用较为广泛。另外,辅助角公式应用也较多,也是考生常出错的地方,应引起注意。
3, 提高学生解决常见综合题的能力,提高运用所学知识分析、提取解题信息的能力。
4, 提高学生的运算和表达的能力,以及确定运算方向和实现转化的能力。
6,三角形中的三角函数问题,要注意正弦定理、余弦定理是实现“边角互换”的关键,而三角变换是解决问题的重要手段。解三角形涉及的变换较多,综合性强,对考生的应变能力和计算能力要求较高,一定要注意控制难度。