08年深圳市高考理科数学联考试题(理)
2008.2
本试卷分第I卷(选择题共40分)和第II卷(非选择题共110分)两部分。考试时间为120分钟,满分为150分。
第一部分 选择题 (共40分)
一、选择题(本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的
1.已知i是虚数单位,那么![]() ( )
( )
A.i B.-i C.1 D.-1
2.命题“![]() ”的否定为
( )
”的否定为
( )
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D)
![]()
3. 设向量![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() =(2,1),
=(2,1),![]() +3
+3![]() =(5,4),则
=(5,4),则![]() =( )
=( )
![]() .
.![]()
![]() .
. ![]()
![]() .
.![]()
![]() .
.![]()
4.在等差数列{an}中,![]()
![]() 则此数列前30项和等于
( )
则此数列前30项和等于
( )
(A)810 (B)840 (C)870 (D)900
5.化简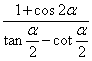 的结果为
( )
的结果为
( )
A. ![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
6.函数f ( x ) = Asin
(![]() x +
x +![]() )( A>0,
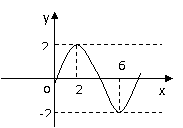
)( A>0,![]() >0)的部分图象如图
>0)的部分图象如图
所示,则f ( 1 ) + f ( 2 ) + … + f ( 2 006 )的值等于( )
 A.0 B.
A.0 B.![]()
C.2 +![]() D.2–
D.2–![]()
7.若函数f ( x
) = min {3 + log![]() x ,log2 x},其中min{p,q}表示p,q两者中的较小者,则f ( x )<2的解集为
( )
x ,log2 x},其中min{p,q}表示p,q两者中的较小者,则f ( x )<2的解集为
( )
A.(0,4) B.(0,+∞)
C.(0,4)∪(4,+∞) D.(![]() ,+∞)
,+∞)
8.对一切实数x,不等式![]() 恒成立,则实数a的取值范围是 ( )
恒成立,则实数a的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第二部分 非选择题(共110分)
二.填空题:每小题5分, 共30分.
9.在各项都为正数的等比数列{an}中,首项a1=3,前三项和为21,则a3+a4+a5=_____________________
10.由曲线![]() 所围成的图形面积是
.
所围成的图形面积是
.
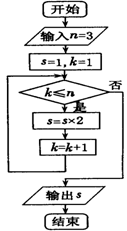 11.右图所示的程序框图的输出结果为
11.右图所示的程序框图的输出结果为
12.若x、y满足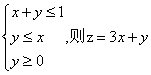 的最大值是
.
的最大值是
.
选做题:在下面三道小题中选做两题,三题都选只计算前两题的得分.
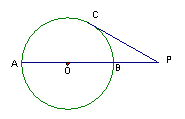 13.如图AB是⊙O的直径,P为AB延长线上一点,PC切⊙O于点C,PC=4,PB=2。则⊙O的半径等于
;
13.如图AB是⊙O的直径,P为AB延长线上一点,PC切⊙O于点C,PC=4,PB=2。则⊙O的半径等于
;
14. 已知![]() 都是正数,且
都是正数,且![]() 则
则![]() 的最小值是
.
的最小值是
.
15.在直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 是参数),若以
是参数),若以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,则曲线
轴的正半轴为极轴,则曲线![]() 的极坐标方程可写为________________.
的极坐标方程可写为________________.
三、解答题:本大题共6小题,共80分. 解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)已知 ![]() =1,
=1,![]() =
=![]() ,
,
(I)若![]() //
//![]() ,求
,求![]() ˙
˙![]() ;(II)若
;(II)若![]() ,
,![]() 的夹角为135°,求
的夹角为135°,求 ![]() +
+![]() .
.
17. (本小题满分13分)已知f ( x ) = 2cos![]() sin
sin![]() –
–![]() .
.
(1)求函数f ( x )的最小正周期,及取得最大值时x的取值集合;
(2)求函数f ( x )图象的对称轴方程;
(3)经过怎样的平移变换和伸缩变换才能使y = f ( x )的图象变为y = cos x 的图象?
18(本小题满分13分)设![]() 是公比大于1的等比数列,
是公比大于1的等比数列,![]() 为数列
为数列![]() 的前
的前![]() 项和.已知
项和.已知![]() ,
,
且![]() 构成等差数列.
构成等差数列.
(1)求数列![]() 的通项;
的通项;
(2)令![]() 求数列
求数列![]() 的前
的前![]() 项和
项和![]() .
.
19.(本小题满分13)
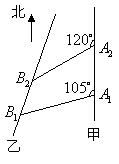 如图,甲船以每小时
如图,甲船以每小时![]() 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于![]() 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西![]() 方向的
方向的![]() 处,此时两船相距
处,此时两船相距![]() 海里,当甲船航行
海里,当甲船航行![]() 分钟到达
分钟到达![]() 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西![]() 方向的
方向的![]() 处,此时两船相距
处,此时两船相距![]() 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
20.(本小题满分14分)
已知![]() 的图象过点(—2,—3),且满足
的图象过点(—2,—3),且满足![]() 设
设![]() 。
。
(Ⅰ)求![]() 的表达式;
的表达式;
(Ⅱ)是否存在正实数![]() ,使
,使![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数?若存在,求出
上是减函数?若存在,求出![]() ;若不存在,请说明理由。
;若不存在,请说明理由。
21. (本小题满分15分)
设函数![]() 的定义域为R,当x<0时
的定义域为R,当x<0时![]() >1,且对任意的实数x,y∈R,有
>1,且对任意的实数x,y∈R,有![]()
(Ⅰ)求![]() ,判断并证明函数
,判断并证明函数![]() 的单调性;
的单调性;
(Ⅱ)数列![]() 满足
满足![]() ,且
,且![]()
①求![]() 通项公式。
通项公式。
②当![]() 时,不等式
时,不等式![]() 对不小于2的正整数n恒成立,求x的取值范围。
对不小于2的正整数n恒成立,求x的取值范围。
2008届高三月考联考数学试卷参考答案
一、选择题(每小题5分,共40分.请把正确选择支号填在答题表内.)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | D | A | D | B | A | B | C | B |
二、填空题(每小题5分,共30分):
9._________84_______;10._____e-2______;11._____8_________________;
12.________3__________;13.________3__________;
14._______![]() _____;15._________
_____;15._________![]() _____
_____
三、解答题:本大题共6小题,共80分. 解答应写出文字说明、证明过程或演算步骤.
16(本小题满分12分)
解(I)∵![]() //
//![]() ,
,
①若![]() ,
,![]() 共向,则
共向,则 ![]() =
=![]() •
•![]() =
=![]() ………………… 3′
………………… 3′
②若![]() ,
,![]() 异向,则
异向,则 ![]() =-
=-![]() •
•![]() =-
=-![]() ……………… 6′
……………… 6′
(II)∵![]() ,
,![]() 的夹角为135°, ∴
的夹角为135°, ∴ ![]() =
=![]() •
•![]() •cos135°=-1 …… 8′
•cos135°=-1 …… 8′
∴![]() +
+![]() 2=(
2=(![]() +
+![]() )2 =
)2 =![]() 2+
2+![]() 2+2
2+2![]() =1+2-2=1 ………… 11′
=1+2-2=1 ………… 11′
∴![]() ……………………………………12
……………………………………12
17. (本小题满分13分)
解:(1)函数可化简为f ( x ) = cos![]() ,
3分
,
3分
最小正周期为![]()
![]() ;
4分
;
4分
当![]() 时,f ( x )取得最大值1
5分
时,f ( x )取得最大值1
5分
取得最大值时x的取值集合为![]() 6分
6分
(2)由![]() 得对称轴方程为:
得对称轴方程为:![]() ,其中
,其中![]() 9分
9分
(3)由于f ( x ) = cos![]() ,
,
把f ( x )图像上各点向左平移![]() 个单位,得到
y=cos2x
11分
个单位,得到
y=cos2x
11分
再把所得图像上各点的横线坐标缩短到原来的2倍,纵坐标不变,得到y=cosx 13分
18. (本小题满分13分)
解:(1)由已知得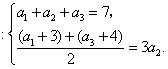 解得
解得![]() .…………………1分
.…………………1分
设数列![]() 的公比为
的公比为![]() ,由
,由![]() ,可得
,可得![]() .
.
又![]() ,可知
,可知![]() ,即
,即![]() , ……………………………3分
, ……………………………3分
解得![]() .
.
由题意得![]() .
. ![]() .………………………………………………………………………
5分
.………………………………………………………………………
5分
故数列![]() 的通项为
的通项为![]() . … ……………………………………………………………………………7分
. … ……………………………………………………………………………7分
(2)由于![]() 由(1)得
由(1)得![]()
![]() ………………………………………………………………………………9分
………………………………………………………………………………9分
又![]()
![]() 是等差数列.
………………………………………………………………………………11分
是等差数列.
………………………………………………………………………………11分
![]()
![]() ………………………………………………13分
………………………………………………13分
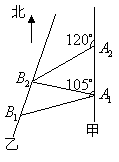 19(本小题满分13分)
19(本小题满分13分)
解:如图,连结![]() ,由已知
,由已知![]() ,。。。。。。。1分
,。。。。。。。1分
![]() , 。。。。。。。。。。2分
, 。。。。。。。。。。2分
![]() ,
,
又![]() ,。。。。。3分
,。。。。。3分
![]() 是等边三角形, 。。。。。4分
是等边三角形, 。。。。。4分
![]() ,
,
由已知,![]() ,
,
![]() ,。。。。。。。。。6分
,。。。。。。。。。6分
在![]() 中,由余弦定理,
中,由余弦定理,
![]()
![]()
![]() .
。。。。。。。。。。。。。10分
.
。。。。。。。。。。。。。10分
![]() . 。。。。。。。。。。11分
. 。。。。。。。。。。11分
因此,乙船的速度的大小为![]() (海里/小时).。。。。。。12分
(海里/小时).。。。。。。12分
答:乙船每小时航行![]() 海里. 。。。。。。。。。。。。。。。。。。。。。。。。13分
海里. 。。。。。。。。。。。。。。。。。。。。。。。。13分
20.(本小题满分14分)
解:(1)

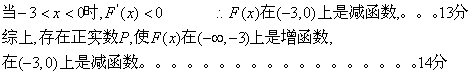
21. (本小题满分15分)
解:(Ⅰ)![]() 时,f(x)>1
时,f(x)>1
令x=-1,y=0则f(-1)=f(-1)f(0)∵f(-1)>1
∴f(0)=1……………………………3′
若x>0,则f(x-x)=f(0)=f(x)f(-x)故![]()
故x∈R f(x)>0…………………………………………………5分
任取x1<x2 ![]()
![]()
故f(x)在R上减函数………………………………………..7分
(Ⅱ)①![]() 由f(x)单调性
由f(x)单调性
………………………………………………………………………………9分
得:an+1=an+2 故{an}等差数列 ![]() ……………………………10分
……………………………10分
②![]()
![]()
![]() 是递增数列
是递增数列
………………………………………………………………………12分
当n≥2时,![]()
![]()
|
即![]()
而a>1,∴x>1
故x的取值范围(1,+∞)……………………………15分
