08年青岛市高考教学第一次统一质量检测
数学试题(文科) 2008.3
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.
注意事项:
1.答卷前,考生务必用2B铅笔和0.5毫米黑色签字笔(中性笔)将姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上。
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。答案不能答在试题卷上。
3.第Ⅱ卷必须用0.5毫米黑色签字笔(中性笔)作答,答案必须写在答题卡各题目指定
区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带。不按以上要求作答的答案无效。
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题.每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.下面框图属于
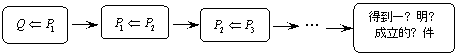 |
A.流程图 B.结构图 C.程序框图 D.工序流程图
3.函数![]() 的图像的两条相邻对称轴间的距离为
的图像的两条相邻对称轴间的距离为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知集合![]() ,
,![]() ,则
,则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.在![]() mL的水中有一个草履虫,现从中随机取出
mL的水中有一个草履虫,现从中随机取出![]() mL水样放到显微镜下观察,则发现草履虫的概率是
mL水样放到显微镜下观察,则发现草履虫的概率是
A.0.001 B.0.002 C.0.004 D.0.005
6.某饭店有![]() 间客房,客房的定价将影响住房率,每天客房的定价与每天的住房率的关系如下表:
间客房,客房的定价将影响住房率,每天客房的定价与每天的住房率的关系如下表:
| 每间客房的定价 |
|
|
|
|
| 每天的住房率 |
|
|
|
|
要使此饭店每天收入最高,则每间客房的定价应为
A.![]() 元 B.
元 B.![]() 元
元
C.![]() 元 D.
元 D.![]() 元
元
 7.图中所示的是一个算法的流程图,已知
7.图中所示的是一个算法的流程图,已知![]() ,输出
,输出
的结果为![]() ,则
,则![]() 的值是
的值是
A.9 B.10 C.11 D.12
8.已知奇函数![]() 对任意的正实数
对任意的正实数![]()
恒有![]() ,则一定正确的是
,则一定正确的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.若![]() 、
、![]() 满足约束条件
满足约束条件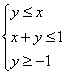 ,则
,则![]() 的最大值为
的最大值为
A.2 B.3 C.4 D.5
10.已知动圆过点![]() ,且与直线
,且与直线![]() 相切,则动圆圆心的轨迹方程为
相切,则动圆圆心的轨迹方程为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.设![]() 、
、![]() 表示两条直线,
表示两条直线,![]() 、
、![]() 表示两个平面,下列命题中真命题的是
表示两个平面,下列命题中真命题的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.符号![]() 表示不超过
表示不超过![]() 的最大整数,如
的最大整数,如![]() ,
,![]() ,定义函数
,定义函数![]() .
.
给出下列四个命题:①函数![]() 的定义域是R,值域为
的定义域是R,值域为![]() ;②方程
;②方程![]() 有无数个解;
有无数个解;
③函数![]() 是周期函数;④函数
是周期函数;④函数![]() 是增函数.其中正确命题的序号有
是增函数.其中正确命题的序号有
A.②③ B.①④ C.③④ D.②④
第Ⅱ卷(非选择题 共90分)
二、填空:本大题共4小题,每小题4分,共16分.
13.命题“若![]() 则
则![]() ”的否命题为 .
”的否命题为 .
14.函数![]() 的零点个数为 .
的零点个数为 .
15.已知函数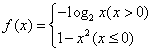 ,则不等式
,则不等式![]() 的解集为
.
的解集为
.
16.给出命题:①函数![]()
![]() R)的最小值等于
R)的最小值等于![]() ;②函数
;②函数![]() 是周期为
是周期为![]() 的奇函数;③函数
的奇函数;③函数![]() 在区间
在区间![]() 上是单调递增的;④若
上是单调递增的;④若![]() ,则
,则![]() 一定为第二象限角.则正确命题的序号是 .
一定为第二象限角.则正确命题的序号是 .
三、解答题:本大题共6小题,共74分,解答时应写出必要的文字说明、证明过程或演算步骤.
17.(本小题共12分) 在![]() 中,
中,![]() 为它的三个内角,设向量
为它的三个内角,设向量![]() 且
且![]() 与
与![]() 的夹角为
的夹角为![]() .
.
(Ⅰ)求角![]() 的大小;
的大小;
(Ⅱ) 已知![]() ,求
,求![]() 的值.
的值.
18.(本小题共12分) 某电信部门执行的新的电话收费标准中,其中本地网营业区内的通话费标准:前3分钟为0.20元(不足3分钟按3分钟计算),以后的每分钟收0.10元(不足1分钟按1分钟计算).在一次实习作业中,某同学调查了![]() 五人某天拨打的本地网营业区内的电话通话时间情况,其原始数据如下表所示:
五人某天拨打的本地网营业区内的电话通话时间情况,其原始数据如下表所示:
| A | B | C | D | E | |
| 第一次通话时间 | 3分 | 3分45秒 | 3分55秒 | 3分20秒 | 6分 |
| 第二次通话时间 | 0分 | 4分 | 3分40秒 | 4分50秒 | 0分 |
| 第三次通话时间 | 0分 | 0分 | 5分 | 2分 | 0分 |
| 应缴话费(元) |
(Ⅰ)在上表中填写出各人应缴的话费;
(Ⅱ)设通话时间为t分钟,试根据上表完成下表的填写(即这五人在这一天内的通话情况统计表):
| 时间段 | 频数累计 | 频数 | 频率 | 累计频率 |
| 0<t≤3 | ┯ | 2 | 0.2 | 0.2 |
| 3<t≤4 | ||||
| 4<t≤5 | ||||
| 5<t≤6 | ||||
| 合计 | 正 正 |
注:累计频率就是样本数据小于某一数值的频率。
 (Ⅲ)若该本地网营业区原来执行的电话收费标准是:每3分钟为0.20元(不足3分钟按3分钟计算).问这五人这天的实际平均通话费与原通话标准下算出的平均通话费相比,是增多了还是减少了?增或减了多少?
(Ⅲ)若该本地网营业区原来执行的电话收费标准是:每3分钟为0.20元(不足3分钟按3分钟计算).问这五人这天的实际平均通话费与原通话标准下算出的平均通话费相比,是增多了还是减少了?增或减了多少?
19.(本小题共12分)如图,在底面是正方形的四棱锥
![]() 中,
中,![]() ,
,![]() .
.
(Ⅰ)证明![]() ;
;
(Ⅱ)已知点![]() 在
在![]() 上,且
上,且![]() ,
,
点![]() 为棱
为棱![]() 的中点,证明
的中点,证明![]()
![]() 平面
平面![]() .
.
20.(本小题共12分)已知函数![]() 在
在![]() 上是增函数.
上是增函数.
(Ⅰ) 求整数![]() 的最大值;
的最大值;
(Ⅱ)令![]() 是(Ⅰ)中求得的最大整数,若对任意的
是(Ⅰ)中求得的最大整数,若对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
21.(本小题共12分)
已知函数![]() 若数列
若数列![]() 成等差数列.
成等差数列.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设数列![]() 对任意的
对任意的![]() 均有
均有![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
22.(本小题共14分)设椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() 、
、![]() ,
,![]() 是椭圆
是椭圆![]() 上的一点,且
上的一点,且![]() ,坐标原点
,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 是椭圆
是椭圆![]() 上的一点,过点
上的一点,过点![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.