08年高考文科数学杭州市第一次教学质量检测
数学试题卷(文科)
考生须知:
1. 本卷满分150分, 考试时间120分钟.
2. 答题前, 在答题卷密封区内填写学校、班级和姓名.
3. 所有答案必须写在答题卷上, 写在试题卷上无效.
4. 考试结束, 只需上交答题卷.
参考公式
如果事件![]() 互斥,那么
互斥,那么![]() ;
;
如果事件![]() 相互独立,那么
相互独立,那么![]() ;
;
如果事件![]() 在一次试验中发生的概率是
在一次试验中发生的概率是![]() ,那么
,那么![]() 次独立重复试验中恰好发生
次独立重复试验中恰好发生![]() 次的概率
次的概率![]() .
.
一. 选择题 : 本大题共10小题, 每小题5分, 共50分. 在每小题给出的四个选项中, 只有一项是符合题目要求的 .
1. 下列4个数中, 最大的是 ( )
(A) ![]() (B)
(B)
![]() (C)
(C) ![]() (D)
(D)
![]()
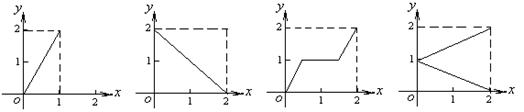
2. 设集合![]() , 那么下面中的4个图形中,
, 那么下面中的4个图形中,
|
① ② ③ ④ (第2题) |
能表示集合![]() 到集合
到集合![]() 的函数关系的有
的函数关系的有
(A) ① ② ③ ④ (B) ① ② ③ (C) ② ③ (D) ②
3. 若![]() 是第三象限的角, 则
是第三象限的角, 则![]() 是 ( )
是 ( )
(A) 第一或第二象限的角 (B) 第一或第三象限的角
(C) 第二或第三象限的角 (D) 第二或第四象限的角
4. ![]() 展开式中的常数项是
展开式中的常数项是
(A) 15 (B) 20 (C) 1 (D) 6
5. 已知在矩形![]() 中,
中, ![]() , 则
, 则![]() 的模等于
的模等于
(A) 4
(B) 5
(C) ![]() (D)
(D)
![]()
6. 已知正数![]() 满足
满足![]() , 则
, 则![]() 的最小值为
的最小值为
(A) 6
(B) 5
(C) ![]() (D)
(D) ![]()
7. 甲, 乙两同学下棋, 赢一局得2分, 和一局得1分, 输一局得1分. 连下3局, 得分多者为胜. 则甲取胜的概率是
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D) ![]()
8. 方程 ![]() 有三个不相等的实根, 则
有三个不相等的实根, 则![]() 的取值范围是
的取值范围是
(A) ![]() (B)
(B) ![]() (C)
(C)
![]() (D)
(D) ![]()
9.已知函数![]() . 如果存在实数
. 如果存在实数![]() , 使得对任意的实数
, 使得对任意的实数![]() , 都有
, 都有
![]() , 则
, 则![]() 的最小值是 ( )
的最小值是 ( )
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
10. 设函数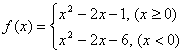 , 若
, 若![]() , 则实数
, 则实数![]() 的取值范围是
的取值范围是
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
二.填空题: 本大题有7小题, 每小题4分, 共28分. 把答案填在答题卷的相应位置.
11. 一个总体含有300个个体,以简单随机抽样方式从该总体中抽取一个容量为20的样
本,则指定的某个个体被抽到的概率为 .
12. 已知等差数列![]() 的前
的前![]() 项和
项和![]() , 则
, 则![]() = ______ .
= ______ .
13. 函数![]() 的定义域是 __________ .
的定义域是 __________ .
14. 若 a =1, b = 2, c = a + b, 且 c ^ a, 则向量a 与b 的夹角为 _____ 度.
15.
已知对任意实数![]() , 有
, 有![]() ,
,![]() ,且
,且![]() 时,
时,
![]() ,
,![]() ,则
,则![]() 时. 应该有
时. 应该有![]() ____
____![]() ,
, ![]() _____
_____![]() .
.
16. 从1到10十个数中,任意选取4个数,其中第二大的数是7的情况共有 _____ 种.
17. 有以下4个结论: ① 若![]() , 那么
, 那么![]() ; ②
; ② ![]() 是函数
是函数![]() 的一条对称轴; ③
的一条对称轴; ③ ![]() 在第四象限是增函数; ④ 函数
在第四象限是增函数; ④ 函数![]() 是偶函数; 其中正确结论的序号是
__________ .
是偶函数; 其中正确结论的序号是
__________ .
三. 解答题: 本大题有5小题, 18至21每小题14分,22题16分, 共72分. 解答应写出文字说明, 证明过程或演算步骤.
18. (本小题满分14分)
已知![]() , 求:
, 求:
(1)
![]() 的值; (2)
的值; (2) ![]() 的值;
的值;
(3)
函数![]() 的图象可以通过函数
的图象可以通过函数![]() 的图象进行怎样的平移得到?
的图象进行怎样的平移得到?
19. (本小题满分14分)
数列![]() 中,
中,![]() ,
, ![]() (
(![]() 是常数,
是常数,![]() ),且
),且![]() 成公比不为
成公比不为![]() 的等比数列.
的等比数列.
(1)求![]() 的值; (2)求
的值; (2)求![]() 的通项公式.
的通项公式.
20 . (本小题满分14分)
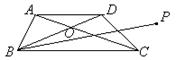
点![]() 是梯形
是梯形![]() 对角线的交点,
对角线的交点, ![]() . 设与
. 设与![]() 同向
同向
|
(第20题) |
的单位向量为a0, 与![]() 同向的单位向量为b0.
同向的单位向量为b0.
(1)
用a0和b0表示![]() 和
和![]() ;
;
(2)
若点![]() 在梯形
在梯形![]() 所在平面上运动, 且
所在平面上运动, 且
![]() , 求
, 求![]() 的最大值和最小值.
的最大值和最小值.
21.(本小题满分14分)
已知关于![]() 的不等式
的不等式![]() .
.
(1) 当![]() 时, 求此不等式的解集;
时, 求此不等式的解集;
(2) 当![]() 时, 求此不等式的解集.
时, 求此不等式的解集.
22. (本小题满分16分)
设函数![]() , 其中
, 其中![]() , 将
, 将![]() 的最小值记为
的最小值记为![]() .
.
(1)求![]() 的表达式;
的表达式;
(2)讨论![]() 在区间[-1,1]内的单调性;
在区间[-1,1]内的单调性;
(3) 若当![]() 时,
时,![]() 恒成立,其中
恒成立,其中![]() 为正数,求
为正数,求![]() 的取值范围.
的取值范围.
数学参考评分标准(文科)
一. 选择题 : (本大题共10小题, 每小题5分, 共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | C | B | A | D | C | C | A | B | D |
二.填空题: (本大题有7小题, 每小题4分, 共28分)
11. ![]() 12.
6
13. (-3,3)
14. 120
12.
6
13. (-3,3)
14. 120
15. ![]() ,
, ![]() 16.
45
17. ① ② ④
16.
45
17. ① ② ④
三. 解答题: (本大题有5小题, 18至21每小题14分,22题16分, 共72分)
18. (本小题满分14分)
(1) ∵![]() , ∴
, ∴![]() , 有
, 有![]() ; --- 4分
; --- 4分
(2) ![]() ;
--- 5分
;
--- 5分
(3) 函数![]() 的图象可以通过函数
的图象可以通过函数![]() 的图象向左平移
的图象向左平移![]() 个单位得到.
个单位得到.
. --- 5分
19. (本小题满分14分)
(1)![]() ,
,![]() ,
,![]() ,
--- 2分
,
--- 2分
∵![]() ,
,![]() ,
,![]() 成等比数列,∴
成等比数列,∴![]() ,
--- 2分
,
--- 2分
解得![]() 或
或![]() , 当
, 当![]() 时,
时,![]() ,不符合题意舍去,故
,不符合题意舍去,故![]() . --- 3分
. --- 3分
(2)当![]() 时,∵
时,∵![]() ,
,![]() ,
,![]()
![]() ,
,
∴![]() .
--- 3分
.
--- 3分
又![]() ,
,![]() ,故
,故![]() .
--- 3分
.
--- 3分
当![]() 时,上式也成立,所以
时,上式也成立,所以![]() . ---
1分
. ---
1分
20 . (本小题满分14分)
(1)
由题意知![]() a0,
a0, ![]() b0, ∴
b0, ∴ ![]() 6 a0 - 2 b0;
6 a0 - 2 b0;
∵![]() , ∴
, ∴![]() a0, 则
a0, 则![]() 2
b0 - 6 a0 +
4 a0 = 2
b0 - 2 a0 ;
2
b0 - 6 a0 +
4 a0 = 2
b0 - 2 a0 ;
--- 4分
∵![]() , ∴
, ∴![]() ,
,
则![]() (6 a0 - 2 b0) =
(6 a0 - 2 b0) = ![]() a0
a0 ![]() b0 .
--- 4分
b0 .
--- 4分
(2) 由题意知点![]() 是在以点
是在以点![]() 为圆心, 3为半径的圆周上运动, 所以由几何意义即得
为圆心, 3为半径的圆周上运动, 所以由几何意义即得![]() 的最大值和最小值分别应该为8和4.
--- 6分
的最大值和最小值分别应该为8和4.
--- 6分
21.(本小题满分14分)
(1) 当![]() 时, 不等式化为
时, 不等式化为![]() , ---
2分
, ---
2分
所以不等式的解集为
![]() ;
--- 3分
;
--- 3分
(2) 当![]() 时, 不等式可化为
时, 不等式可化为![]() ,
--- 3分
,
--- 3分
当![]() 时, 解集为
时, 解集为![]() ;
--- 2分
;
--- 2分
当![]() 时, 解集为
时, 解集为 ![]() ;
--- 2分
;
--- 2分
当![]() 时, 解集为
时, 解集为 ![]() .
--- 2分
.
--- 2分
22.(本小题满分16分)
(1) ![]() , 当
, 当![]() 时,
时, ![]() 达到其最小值
达到其最小值![]() ,即
,即
![]() ;
--- 4分
;
--- 4分
(2)因为![]() ,
,
列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 | 极小值 |
由此可见,![]() 在区间
在区间![]() 和
和![]() 单调递增,在区间
单调递增,在区间![]() 单调递减; --- 6分
单调递减; --- 6分
(3) ![]()
![]() ,所以
,所以![]() ;
;
又![]()
![]() 既
既![]() 恒成立,所以
恒成立,所以![]() ,综合可得k的范围为:
,综合可得k的范围为:![]() .
.
--- 6分