08年高考文科数学模拟考试题卷
第Ⅰ卷（选择题 共50分）
一、选择题（本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。）
1．已知集合P={ 0,
m},Q={x│
},若P∩Q≠
,则m等于（ ）
A.1
B.2
C.1或
D. 1或2
2．将函数
的图象按向量
平移后所得图象的解析式是（ ）
A．
B．
C．
D．
3．数列{an}前n项和Sn = 3n– t，则t = 1是数列{an}为等比数列的( )
A．充分不必要 B．必要不充分
C．充要条件 D．既不充分又不必要
4. 函数
的反函数是（ ）
A．
B．
C．
D．
5．某球与一个120°的二面角的两个面相切于A、B，且A、B间的球面距离为
，则此球体的表面积为（ ）
A．
B．
C．
D．
6．设下表是某班学生在一次数学考试中数学成绩的分布表
| 分数 |
|
|
|
|
|
|
|
|
| 人数 | 2 | 5 | 6 | 8 | 12 | 6 | 4 | 2 |
，
，
，
，
，
，
，
，
那么分数在[100，110]中和分数不满110分的频率和累积频率分别是（ ）．
A．0.18，0.47 B．0.47，0.18 C．0.18，1 D．0.38，1
7．设ｆ(x)= x2+ax+b，且1≤f(－1)≤2，2≤f(1)≤4，则点(a，b)在aOb平面上的区域面积是 （ ）
A．
B．1
C．2
D．
8．已知P是以F1、F2为焦点的椭圆
上一点，若
=0， 
=2，则椭圆的离心率为（ ）
A． 
B． 
C． 
D． 
9．设
，
在
上的投影为
，在
轴上的投影为2，且
，则为（ ）
A．
B．
C．
D．
10. 过抛物线y2 = 2ρx (ρ＞0 )上一定点M ( x0,y0
) ( y0≠0 )，作两条直线分别交抛物线于A ( x1 , y1
) , B ( x2 , y2 )，当MA与MB的斜率存在且倾斜角互补时，则
= （ ）
A．4 B．– 4 C．2 D．–2
第Ⅱ卷（非选择题 共100分）
二、填空题：(本大题共5小题，每小题5分，共25分．把答案填在答题卡相应位置上．)
11．设常数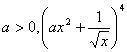
展开式中
的系数为
则
= ______
12．由直线
上的一点向圆
引切线，则切线长的最小值为______
13．将4个相同的白球、5个相同的黑球、6个相同的红球放入4个不同盒子中的3个中，使得有1个空盒且其它盒子中球的颜色齐全的不同放法共有种.（用数字作答）
14．某篮球运动员在罚球线投中球的概率为
，在某次比赛中罚3球恰好命中2球的概率为
__________________。
15．给出下列四个命题：
①过平面外一点，作与该平面成θ角的直线一定有无穷多条；
②一条直线与两个相交平面都平行，则它必与这两个平面的交线平行；
③对确定的两条异面直线，过空间任意一点有且只有唯一的一个平面与这两条异面直线都平行；
④对两条异面的直线，都存在无穷多个平面与这两条直线所成的角相等；
其中正确的命题序号为 （请把所有正确命题的序号都填上）．
三、解答题：(本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤．)
16.(本小题满分12分)
、
、
为
的三内角，且其对边分别为、
、
，若
，
，且
（1）求角；
（2）若
，三角形面积
，求
的值．
17．（本小题满分12分）
已知数列 {2 n•an} 的前 n 项和 Sn = 9－6n.
(I) 求数列 {an} 的通项公式；
(II) 设 bn = n·(2－log 2 )，求数列 { } 的前 n 项和Tn.
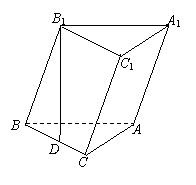
18．（本小题满分12分）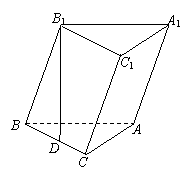 
已知斜三棱柱ABC—A1B1C1的底面是直角三角形，∠C=90°，侧棱与底面所成的角为α（0°＜α＜90°），点
在底面上的射影
落在
上．
（Ⅰ）求证：AC⊥平面BB1C1C；
（Ⅱ）当α为何值时，AB1⊥BC1，且使D恰为BC中点？
（Ⅲ）若α = arccos ，且AC=BC=AA1时,求二面角C1—AB—C的大小．
19．(本小题满分12分)
随着我国加入WTO，某企业决定从甲、乙两种产品中选择一种投资生产，打入国际市场，已知投资生产这两种产品的有关数据如下表：(单位：万美元)
|
| 年固定成本 | 每件产品成本 | 每件产品销售价 | 最多可生产件数 |
| 甲产品 | 20 | a | 10 | 200 |
| 乙产品 | 40 | 8 | 18 | 120 |
其中年固定成本与年生产的件数无关，a 为常数，且 3≤a≤8.另外，年销售 x件乙产品时需上交 0.05x 2万美元的特别关税.
(I) 写出该厂分别投资生产甲、乙两产品的年利润 y1、y2 与生产相应产品的件数 x(x∈N)之间的函数关系；
(II) 分别求出投资生产这两种产品的最大年利润；
(III) 如何决定投资可获最大年利润.
20．（本小题满分13分）
设
，其导函数
的图像经过点
，且
在
时取得最小值－8
（1）求的解析式；
（2）若对
都有
恒成立，求实数
的取值范围．
21．（本小题共14分）已知
是双曲线
上两点，
为原点，直线
的斜率之积
（Ⅰ）设
，证明当运动时，点
恒在另一双曲线上；
（Ⅱ）设
，是否存在不同时为零的实数
，使得点
在题设双曲线的渐近线上，证明你的结论.
08年高考文科数学模拟考试题卷
参考答案
一、选择题：（本大题共10个小题；每小题5分，共50分。）
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 | D | A | C | A | C | A | B | D | B | D |
二、填空题：（本大题共5小题，每小题5分，共25分。）
11、
； 12、
； 13、720； 14 、
； 15、②④；
三、解答题：（本大题共6小题，共75分。）
16、（本小题满分12分）
解：（1）∵，，且
∴
…………………………………………2分
即
又
，∴
……………………………5分
⑵
，∴
＝4
……………………………7分
由余弦定理得
……………………………10分
∴
故
． ………………………………12分
17、（本小题满分12分）
解：(I) n = 1 时，2·a1 = S1 = 3,∴a1 = ; …………2分
当 n≥2 时，2 n·an = Sn－Sn－1 = －6，∴ an = . 又 ≠ …………4分
∴ 通项公式an = …………6分
(II)当 n = 1 时，b1 = 2－log 2 = 3，∴ T1 = = ； …………8分
n≥2时， bn = n·(2－log 2) = n·(n + 1)， ∴ = …………10分
∴ Tn = + + … + = + + + … + = －
∴ Tn = － …………12分
18、（本小题满分12分）
解：（Ⅰ）∵
B1D⊥平面ABC， AC
平面ABC，
∴ B1D⊥AC, 又AC⊥BC, 
BC∩B1D=D．
∴ AC⊥平面BB1C1C． …………………… 3分
(Ⅱ) ∵ AC⊥平面BB1C1C ，要使AB1⊥BC1 ，由三垂线定理可知，
只须B1C⊥BC1， ………………………… 5 分
∴ 平行四边形BB1C1C为菱形， 此时，BC=BB1．
又∵ B1D⊥BC, 要使D为BC中点，只须B1C= B1B，即△BB1C为正三角形， ∴ ∠B1BC= 60°． ………………………… 7分
∵ B1D⊥平面ABC，且D落在BC上，
∴ ∠B1BC即为侧棱与底面所成的角．
故当α=60°时，AB1⊥BC1，且使D为BC中点…………………… 8分
（Ⅲ）过C1作C1E⊥BC于E，则C1E⊥平面ABC．
过E作EF⊥AB于F，C1F，由三垂线定理，得C1F⊥AB．
∴∠C1FE是所求二面角C1—AB—C的平面角．………………… 10分
设AC=BC=AA1=a，
在Rt△CC1E中，由∠C1BE=α=
，C1E=
a．
在Rt△BEF中，∠EBF=45°，EF=
BE=a．
∴∠C1FE=45°，故所求的二面角C1—AB—C为45°．………… 12分
解法二：（1）同解法一 ……………… 3分
（Ⅱ）要使AB1⊥BC1，D是BC的中点，即
=0，=，
∴
， 
=0，∴
．
∴
，故△BB1C为正三角形，∠B1BC=60°；
∵ B1D⊥平面ABC，且D落在BC上， …………………… 7分
∴ ∠B1BC即为侧棱与底面所成的角．
故当α=60°时，AB1⊥BC1，且D为BC中点． …………………8分
（Ⅲ）以C为原点，CA为x轴，CB为y轴，经过C点且垂直于平面ABC的直线为z轴建立空间直角坐标系，则A（a，0，0），B（0，a，0），C（0，－
，a），
平面ABC的法向量n1=（0，0，1），设平面ABC1的法向量n2=（x，y，z）．
由
n2=0，及
n2=0，得
∴n2=（
，，1）．………………10分
cos<n1, n2>＝= ，
故n1 , n2所成的角为45°，即所求的二面角为45°．……………………12分
19、（本小题满分12分）
解：(I)由年销售量为 x件，按利润的计算公式，有生产甲、乙两产品的年利润 y1， y2分别为：
y1 = 10×x－(20 + ax) = (10－a)x－20， 0≤x≤200且 x∈N…………1分
y2 = 18×x－(40 + 8x) － 0.05x 2 = －0.05x 2 + 10x－40，…………2分
∴ y2 = －0.05 (x－100) 2 + 460，0≤x≤120，x∈N…………3分
(II) ∵ 3≤a≤8， ∴ 10－a > 0， ∴ y1 = (10－a)x－20为增函数，
又 0≤x≤200，x∈N
∴ x = 200时，生产甲产品的最大年利润为 (10－a)×200－20 = 1980－200a(万美元)。…………5分
又 y2 = －0.05 (x－100) 2 + 460，且 0≤x≤120，x∈N
∴ x = 100时，生产乙产品的最大年利润为 460(万美元)。…………7分
(III) 问题即研究生产哪种产品年利润最大，
(y1)max－(y2)max = (1980－200a) －460 = 1520－200a …………10分
所以：当 3≤a < 7.6时，投资生产甲产品 200件可获最大年利润。
当 a = 7.6时，生产甲产品与生产乙产品均可获得最大年利润；
当 7.6 < a≤8时，投资生产乙产品 100件可获最大年利润。……12分
20、（本小题满分13分）
解：（1）
，且的图像经过点,
∴
，
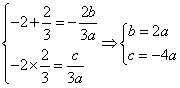……2分∴
， ……3分
由
，解得
…5分∴
……6分
（2）要使对都有恒成立，只需
即可．
…………………………7分
∵
…………………………8分
∴函数
在
上单调递减，在
上单调递增，在
上单调递减，…………………………10分
又∵
，
，
∴
； 
故所求的实数的取值范围为
．
…………………………13分
21. （本小题满分14分）
解：（Ⅰ）设
，由 ，得
由在双曲线上，有
①
②…………………………………………2分
由，即
，
得
， ③………………………………………4分
①+2×③+②，并整理，得
这表明点恒在双曲线
上.……………………………6分
（Ⅱ）同（Ⅰ）所设，由
，得
当点在双曲线的渐近线上，有
即
，亦即
…………………10分
将①②③三式代入上式，得
，从而
因此，不存在不同时为零的实数，使得点在题设双曲线的渐近上.…14分