08届高考文科数学模拟测试试题(一)
数学(文科)
注意事项:
1.本试卷分为选择题和非选择题两部分,共7页。
2.答卷前,考生务必将自己的姓名、座号、准考证号分别填写在答题卡及答题纸上。
3.选择题的每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号,不能答在试卷上。
4.考试结束后,将答题卡和答题纸一并交回。
第Ⅰ卷 选择题(共60分)
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合M=![]() ,N=
,N=![]() ,则集合
,则集合![]() =( )
=( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2.函数![]() 的最小正周期是( )
的最小正周期是( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.
![]()
3.若A、B、C是锐角三角形ABC的三个内角,向量![]() =(sinA,cosA),
=(sinA,cosA),![]() =(sinB,−cosB),则
=(sinB,−cosB),则![]() 与
与![]() 的夹角为( )
的夹角为( )
A.锐角 B.直角 C.钝角 D.以上都不对
4.已知抛物线![]() ,则它的准线方程为( )
,则它的准线方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5. 在等差数列![]() 中,公差d=1,
中,公差d=1,![]() ,则
,则![]() 的值为( )
的值为( )
A.40 B.45 C.50 D.55
6.若P为双曲线![]() 右支上一点,P到右准线的距离为
右支上一点,P到右准线的距离为![]() ,则点P到双曲线左焦点的距离为(
)
,则点P到双曲线左焦点的距离为(
)
A.1 B.2 C.6 D.8
7.记函数![]() 的反函数为y=g(x),则g(5)等于( )
的反函数为y=g(x),则g(5)等于( )
A.2 B.-2 C.-4 D.4
8.某校高一、高二年级各有300人,高三年级有400人,现采用分层抽样抽取容量为50人的样本,那么高三年级应出人数为( )
A.16 B.40 C.20 D.25
9.![]() ,且关于x的方程
,且关于x的方程![]() 有实根,则
有实根,则![]() 与
与![]() 夹角的取值范围是( )
夹角的取值范围是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10.若实数x,y满足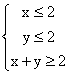 ,则x+2y的最小值和最大值分别为( )
,则x+2y的最小值和最大值分别为( )
A.2,6 B.2,5 C.3,6 D.3,5
11.在正三棱柱![]() 中,若
中,若![]() ,
,![]() ,则点
,则点![]() 到平面
到平面![]() 的距离为( ) (A)
的距离为( ) (A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
12、非零向量![]() ,若点B关于
,若点B关于![]() 所在直线的对称点为
所在直线的对称点为![]() ,则向量
,则向量![]() 为( )
为( )
A、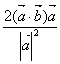 B、
B、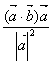 C、
C、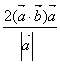 D、
D、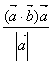
第Ⅱ卷 非选择题(共90分)
二.填空题(4×4′=16分):
13.![]() ;
;
14.已知n为等差数列−4,−2,0,…,中的第8项,则二项式![]() 展开式中的常数项是 ;
展开式中的常数项是 ;
15.若一个圆的圆心在抛物线![]() 的焦点上,且此圆与直线
的焦点上,且此圆与直线![]() 相
相
切,则这个圆的方程是 ;
16.已知m、n为直线,α,β为平面,给出下列命题:
①![]() ②
②![]() ③
③![]() ④
④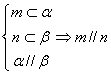
其中的正确命题序号是:
三.解答题(满分74分):
17(本题12分).已知![]() ,
,![]() ,记函数
,记函数![]()
(1)求函数![]() 的最小正周期及最值;
的最小正周期及最值;
(2)当![]() 时,求函数
时,求函数![]() 的值域.
的值域.
18(本题12分).甲、乙两人同时参加一次面试,已知在备选的10道试题中,甲能答对其中的6道,乙能答对其中的8道,规定每次考试都从备选题中随机抽出3道题进行测试,至少答对2道题才算通过。求:
(Ⅰ)甲答对两道题的概率;
(Ⅱ)甲、乙两人至少有一人通过面试的概率.
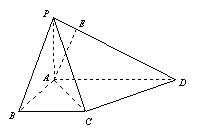 19(本题12分).如图,在四棱锥
19(本题12分).如图,在四棱锥![]() 中,底面
中,底面![]() 是一直角梯形,
是一直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 平面
平面![]() ,
,![]() 与底面成
与底面成![]() 角.
角.
(Ⅰ) 求证:平面![]() 平面
平面![]() ;
;
(Ⅱ) 求二面角![]() 的一个三角函数值;
的一个三角函数值;
20(本题12分).设函数![]() ,其中
,其中![]()
(Ⅰ)若f(x)在x=3处取得极值,求常数a 的值;
(Ⅱ)若f(x)在![]() 上为增函数,求a的取值范围
上为增函数,求a的取值范围
21(本题12分).已知数列![]() 的前n项和
的前n项和![]() 满足
满足![]() ,且
,且![]()
(1)
求![]() ;
;
(2)
求![]() 的通项公式;
的通项公式;
(3)令![]() ,问数列
,问数列![]() 的前多少项的和最大?
的前多少项的和最大?
22(本题14分).在直角坐标系中,![]() 为坐标原点,设直线
为坐标原点,设直线![]() 经过点
经过点
![]() (3,
(3,![]() ),且与
),且与![]() 轴交于点
轴交于点![]()
(1)求直线![]() 的方程;
的方程;
(2)若一个椭圆经过点![]() ,且以点
,且以点![]() 为它的一个焦点,求椭圆的标准方程;
为它的一个焦点,求椭圆的标准方程;
(3)若在(1)(2)的情况下,设直线![]() 与椭圆的另一个交点
与椭圆的另一个交点![]() ,且
,且![]() ,
,
当|![]() |最小时,求
|最小时,求![]() 对应值.
对应值.
08届高考文科数学模拟测试试题(一)(文)
(参考答案及评分细则)
一.选择题:DCADB DBCBA BA
二.填空题:13、![]() ,14、45,15、
,14、45,15、![]() 16、②、③
16、②、③
三.解答题:
17.解:(1)![]() 2分
2分
=![]() 4分=
4分=![]() 6分
6分
所以![]() ,
,![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() 7分
7分
(2)当![]() ,即
,即![]() ,有
,有![]() 10分
10分
所以当![]() ,函数
,函数![]() 的值域为
的值域为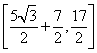 12分
12分
18.解:(Ⅰ)P(ξ=2)=![]() ,.……………………(3分)
,.……………………(3分)
(Ⅱ)甲未通过的概率为:p1=![]() ……………………(8分)
……………………(8分)
乙未通过的概率为:p2=![]() ……………………………(10分)
……………………………(10分)
∴甲、乙两人至少有一人通过面试的概率为:![]() =
=![]() …(12分)
…(12分)
19.(1)略(2)tan![]() =
=![]()
20.解:(1)![]() (2分)
(2分)
因![]() 在x=3处取得极值,所以
在x=3处取得极值,所以![]() 解得a=3 (4分)
解得a=3 (4分)
经检验知当a=3时,x=3为f(x)的极值点。 (6分)
(2)由![]() =0得
=0得![]() 。当a<1时,若
。当a<1时,若![]() ,则
,则![]() ,所以f(x)在
,所以f(x)在![]() 和(1,+
和(1,+![]() )上为增函数,故当
)上为增函数,故当![]() 时,f(x)在(
时,f(x)在(![]() 为增函数;
(8分)
为增函数;
(8分)
当![]() 时,若
时,若![]() ,则
,则![]() ,所以f(x)在
,所以f(x)在![]() 和(a,+
和(a,+![]() )上为增函数,故f(x)在(
)上为增函数,故f(x)在(![]() 上也为增函数
(10分)
上也为增函数
(10分)
综上所述:当![]() 时,f(x)在
时,f(x)在![]() 上为增函数
上为增函数
21.解:(1)![]() ,
,![]() (4分)
(4分)
(2)当![]() 时,
时,![]() =
=![]()
由此得![]() ,
,![]() 公差为2的等差数列,故
公差为2的等差数列,故![]() (8分)
(8分)
(3)由于![]() ,故当n=10时,
,故当n=10时,![]() 最大
(12分)
最大
(12分)
22. 解:(14分)(1)∵![]() (3,
(3,![]() ),
),![]() (2,0),
(2,0),
∴根据两点式得,所求直线![]() 的方程为
的方程为![]() =
=![]() 即
即![]() ∴直线
∴直线![]() 的方程是
的方程是![]() (4分)
(4分)
(3)
解:设所求椭圆的标准方程为![]() =1(
=1(![]() )
)
∵![]() (4分)∴椭圆的另一个焦点为
(4分)∴椭圆的另一个焦点为![]() (-2,0)由椭圆过点
(-2,0)由椭圆过点
![]() (3,
(3,![]() ),∴
),∴![]() +
+![]() =4
=4![]()
∴![]() 所以所求椭圆的标准方程为
所以所求椭圆的标准方程为![]() =1.
(9分)
=1.
(9分)
(4)
解:由题意得方程组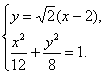 解得
解得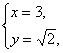 或
或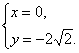
∴![]() (0,2
(0,2![]() )(10分)
)(10分)![]() =(-3,-3
=(-3,-3![]() ).∵
).∵![]() =λ
=λ![]() =(-3λ,3
=(-3λ,3![]() λ),
λ),
∴![]() =
=![]() +
+![]() =(3-3λ,
=(3-3λ,![]() ,3
,3![]() λ).∴
λ).∴![]() =
=![]()
=![]() =
=![]() ,∴当λ=
,∴当λ=![]() 时,
时,![]() 最小 (14分)
最小 (14分)