08届高考文科数学第一次联合考试试卷
注意事项:
1.本试题分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟。
2.请将第I卷选择题的答案填在答题卡上,第II卷在各题后直接作答。
参考公式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)= P(A)+ P(B) S=4πR2
如果事件A、B相互独立, 其中R表示球的半径
那么P(A·B)=P(A)·P(B) 球的体积公式
如果事件A在一次试验中发生的概率 ![]()
是![]() ,那么n次独立重复试验中恰好发 其中R表示球的半径
,那么n次独立重复试验中恰好发 其中R表示球的半径
生k 次的概率
Pn(k)=![]()
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是最符合题目要求的.
1![]() 已知集合M ={
已知集合M ={![]()
![]() <
<![]() },N={x
},N={x![]() },则M ∩N等于
( )
},则M ∩N等于
( )
A![]() Æ B
Æ B![]() {x-1<x<3} C
{x-1<x<3} C![]() {x0<x<3} D
{x0<x<3} D![]() {x1<x<3}
{x1<x<3}
2![]() 某校现有高一学生210人,高二学生270人,高三学生300人,用分层抽样的方法从这三个年级的学生中随机抽取n名学生进行问卷调查,如果已知从高一学生中抽取的人数为7,那么从高三学生中抽取的人数应为
( )
某校现有高一学生210人,高二学生270人,高三学生300人,用分层抽样的方法从这三个年级的学生中随机抽取n名学生进行问卷调查,如果已知从高一学生中抽取的人数为7,那么从高三学生中抽取的人数应为
( )
A![]() 10 B
10 B![]() 9 C
9 C![]() 8 D
8 D![]() 7
7
3![]() 若函数
若函数![]() 的反函数为
的反函数为![]() ( )
( )
A![]() 1 B
1 B![]() 11 C
11 C![]() 1或-1 D
1或-1 D![]() -1
-1
4![]() 在等差数列
在等差数列![]() 中,
中,![]() ,
,![]() ,则数列
,则数列![]() 的前9项之和
的前9项之和![]() 等于
( )
等于
( )
A.66 B.99 C.144 D.297
5![]() 已知
已知![]() 则不等式
则不等式![]() 的解集为
( )
的解集为
( )
A![]()
![]() B
B![]()
![]()
C![]()
![]() D
D![]()
![]()
6![]() 在
在![]() 中,“
中,“![]() ”是“
”是“![]() 为锐角三角形”的( )
为锐角三角形”的( )
A![]() 充分不必要条件 B
充分不必要条件 B![]() 必要不充分条件
必要不充分条件
C![]() 充要条件 D
充要条件 D![]() 既非充分又非必要条件
既非充分又非必要条件
|
A![]()
![]()
B![]()
![]()
C![]()
![]()
D![]()
![]()
8.在![]() 的展开式中,
的展开式中,![]() 的系数为
( )
的系数为
( )
A![]()
![]() 120
B
120
B![]() 120
C
120
C![]()
![]() 15
D
15
D![]() 15
15
9![]() 若直线
若直线![]() 按向量
按向量![]() =(1,
=(1,![]() 1)平移后与圆
1)平移后与圆![]() 相切,则
相切,则![]() 的值为( )
的值为( )
A. 8或![]() 2 B.6或
2 B.6或![]() 4 C.4或
4 C.4或![]() 6 D.2或
6 D.2或![]() 8
8
10![]() 某次文艺汇演,要将A、B、C、D、E、F这六个不同节目编排成节目单,如下表:
某次文艺汇演,要将A、B、C、D、E、F这六个不同节目编排成节目单,如下表:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 节目 |
|
|
|
|
|
|
如果A、B两个节目要相邻,且都不排在第3号位置,那么节目单上不同的排序方式
A![]() 192种 B
192种 B![]() 144种 C
144种 C![]() 96种 D
96种 D![]() 72种
72种
11![]() 已知点
已知点![]() 是以
是以![]() 、
、![]() 为焦点的椭圆
为焦点的椭圆![]() 上的一点,若
上的一点,若![]() ,
,![]() ,则此椭圆的离心率为
( )
,则此椭圆的离心率为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.若关于![]() 的方程
的方程![]() 恒有实数解,则实数m的取值范围是( )
恒有实数解,则实数m的取值范围是( )
A. [0,8] B.[![]() 1,8] C.
[0,5]
D. [
1,8] C.
[0,5]
D. [![]() 1,+∞)
1,+∞)
08届高考文科数学第一次联合考试试卷
| 题 号 | 一 | 二 | 三 | 总分 | ||||||
| 得 分 |
|
|
|
|
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中的横线上.
13![]() 已知
已知![]()
![]()
14![]() 一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为 .
一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为 .
15![]() 已知
已知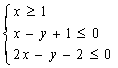 则
则![]() 的最小值是
的最小值是
![]()
16.已知点![]() 在圆
在圆![]() 上运动,当角
上运动,当角![]() 变化时,点
变化时,点![]() 运动区域的面积为
.
运动区域的面积为
.
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
|
(Ⅰ)求甲射击5次,有两次未击中目标的概率;
(Ⅱ)求两人各射击4次,甲恰好击中目标2次,且乙恰好击中目标3次的概率![]()
|
(I)求![]() 的最小正周期及最大值;
的最小正周期及最大值;
(II)求使![]() ≥2的
≥2的![]() 的取值范围
的取值范围
|
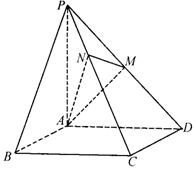
(Ⅰ)求证:![]() ⊥平面
⊥平面![]() ;
;
|
|
(Ⅰ)求![]() ,
,![]() ,
,![]() 的值;
的值;
(Ⅱ)求函数![]() 的单调递增区间,并求函数
的单调递增区间,并求函数![]() 在
在![]() 上的最大值和最小值
上的最大值和最小值 ![]()
|
(Ⅰ)分别求数列![]() ,
,![]() 的通项公式
的通项公式![]() ,
,![]()
![]()
(Ⅱ)设![]() 若
若![]() 恒成立,求c的最小值
恒成立,求c的最小值![]()
|
(Ⅰ)若双曲线过点![]() (
(![]() ,
,![]() ),求双曲线的方程;
),求双曲线的方程;
(Ⅱ)在(Ⅰ)的条件下,若![]() 、
、![]() 是双曲线上不同的两点,且
是双曲线上不同的两点,且![]() ,求直线
,求直线![]() 的方程
的方程![]()
参考答案及评分标准
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | D | B | D | B | C | C | A | B | D | A |
二、填空题:
13.1 14.![]() 15.5 16.
15.5 16.![]()
三、解答题:
17.解:(I)设“甲射击5次,有两次未击中目标”为事件A,则 ![]()
答:甲射击5次,有两次未击中目标的概率为![]()
![]() …………5分
…………5分
(Ⅱ)设“两人各射击4次,甲恰好击中目标2次,且乙恰好击中目标3次”为事件B,则![]()
答:两人各射击4次,甲恰好击中目标2次,且乙恰好击中目标3次的概率为![]()
![]() …10分
…10分
18.解:(I)![]()
![]() ……2分
……2分
![]()
![]() ………………4分
………………4分
![]()
![]() …………………………6分
…………………………6分
(II)由![]() 得
得![]()
![]()
![]()
![]()
![]() 的x的取值范围是
的x的取值范围是![]() …………12分
…………12分
19.解:(Ⅰ)因为四棱锥P—ABCD的底面是正方形,PA⊥底面ABCD,
则CD⊥侧面PAD![]()
![]() 又
又![]()
又![]() ……………5分
……………5分
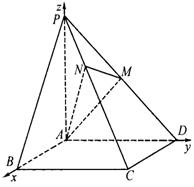
(Ⅱ)建立如图所示的空间直角坐标系![]() 又PA=AD=2,
又PA=AD=2,
则有P(0,0,2),D(0,2,0)![]()
![]()
|
设![]() 则有
则有
![]()
同理可得![]()
即得![]() …………………………8分
…………………………8分
由![]()
![]()
而平面PAB的法向量可为![]()
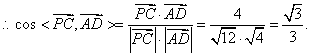
故所求平面AMN与PAB所成锐二面角的大小为![]() …………12分
…………12分
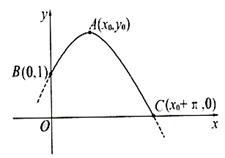
20.解:(Ⅰ)∵![]() 为奇函数,∴
为奇函数,∴![]()
即![]() ∴
∴![]() …………………2分
…………………2分
∵![]() 的最小值为
的最小值为![]() ∴
∴![]()
又直线![]() 的斜率为
的斜率为![]() 因此,
因此,![]()
∴![]() ,
,![]() ,
,![]()
![]() ………………………………………5分
………………………………………5分
(Ⅱ)由(Ⅰ)知![]()
![]()
∴![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大 |
| 极小 |
|
所以函数![]() 的单调增区间是
的单调增区间是![]() 和
和![]() …………8分
…………8分
∵![]() ,
,![]() ,
,![]()
∴![]() 在
在![]() 上的最大值是
上的最大值是![]() ,最小值是
,最小值是![]() ………12分
………12分
21.解:(Ⅰ)设d、q分别为数列![]() 、数列
、数列![]() 的公差与公比.
的公差与公比.
由题可知,![]() 分别加上1,1,3后得2,2+d,4+2d
分别加上1,1,3后得2,2+d,4+2d
是等比数列![]() 的前三项,
的前三项,
![]()
![]()
![]() ……………4分
……………4分
由此可得![]()
![]() …………………………6分
…………………………6分
(Ⅱ)![]() ①
①
当![]() ,
,![]() 当
当![]() ,
,![]() ②
②
①—②,得
![]()
![]()
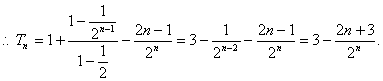 ………………9分
………………9分
![]()
![]() 在N*是单调递增的,
在N*是单调递增的,![]()
∴满足条件![]() 恒成立的最小整数值为
恒成立的最小整数值为![]() ……12分
……12分
22.解:(Ⅰ)∵双曲线方程为 ![]()
∴![]() ,
,
∴双曲线方程为 ![]() ,又曲线C过点Q(2,
,又曲线C过点Q(2,![]() ),
),
∴![]()
∴双曲线方程为 ![]() ………………5分
………………5分
(Ⅱ)∵![]() ,∴M、B2、N三点共线
,∴M、B2、N三点共线![]()
∵![]() , ∴
, ∴![]()
(1)当直线![]() 垂直x轴时,不合题意
垂直x轴时,不合题意![]()
(2)当直线![]() 不垂直x轴时,由B1(0,3),B2(0,-3),
不垂直x轴时,由B1(0,3),B2(0,-3),
可设直线![]() 的方程为
的方程为![]() ,①
,①
∴直线![]() 的方程为
的方程为 ![]() ②
②
由①,②知 ![]() 代入双曲线方程得
代入双曲线方程得
![]() ,得
,得![]() ,
,
解得 ![]() , ∴
, ∴![]() ,
,
故直线![]() 的方程为
的方程为 ![]() ………………12分
………………12分