08届高考文科数学第三次模拟考试试题
一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1![]() 已知
已知![]() 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为![]() ,那么
,那么![]() =
=
A.4 B.![]() C.
C.![]() D.
D.![]()
2![]() 过点
过点![]() 的直线
的直线![]() 经过圆
经过圆![]() 的圆心,则直线
的圆心,则直线![]() 的倾斜角大小为
的倾斜角大小为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3![]() 设函数f( x )的图象关于点(1,
设函数f( x )的图象关于点(1,![]() )对称,且存在反函数
)对称,且存在反函数![]() ( x ),若f(3) = 0,
( x ),若f(3) = 0,
则![]() (3)等于
(3)等于
A.-1 B.1 C.-2 D.2
4![]() 设m,n是两条不同的直线,α、β、γ是三个不同的平面
设m,n是两条不同的直线,α、β、γ是三个不同的平面![]() 给出下列四个命题:
给出下列四个命题:
①若m⊥α,n∥α,则m⊥n; ②若α⊥γ,β⊥γ,则α∥β;
③若m∥α,n∥α,则m∥n; ④若α∥β,β∥γ,m⊥α,,则m⊥γ![]()
其中正确命题的序号是:
A.①和② B.②和③ C.③和④ D.①和④
5.函数y = cos(2x+![]() )的一条对称轴方程是
)的一条对称轴方程是
A.x = -![]() B.x = -
B.x = -![]() C.x = -
C.x = -![]() D.x =
D.x = ![]()
6![]()
![]() ,则“
,则“![]() ”是“
”是“![]() ”的
”的
A.充分非必要条件 B.必要非充分条件
C.充分必要条件 D.既非充分也非必要条件
 7
7![]() 若点
若点![]() 在双曲线
在双曲线![]() 的左准线上,过点
的左准线上,过点![]() 且方向向量为
且方向向量为![]() 的光线,经直线
的光线,经直线![]() 反射后通过双曲线的左焦点,则这个双曲线的离心率为
反射后通过双曲线的左焦点,则这个双曲线的离心率为
A![]()
![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知四面体![]() 中,
中,![]() 与
与![]() 间的距离与夹角分别为3与
间的距离与夹角分别为3与![]() ,则四面体
,则四面体![]() 的体积为
的体积为
A.![]() B.1 C.2 D.
B.1 C.2 D.![]()
9.从1,2,3,4,5 中取三个不同数字作直线![]() 中
中![]() 的值,使直线与圆
的值,使直线与圆![]() 的位置关系满足相离,这样的直线最多有
的位置关系满足相离,这样的直线最多有
A.30条 B.20条 C.18条 D.12条
10.已知等差数列{an}与等差数列{bn}的前n项和分别为Sn和Tn,若![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知点P是抛物线![]() = 2x上的动点,点p在y轴上的射影是M,点A的坐标是
= 2x上的动点,点p在y轴上的射影是M,点A的坐标是![]() ,则 PA + PM 的最小值是
,则 PA + PM 的最小值是
A.![]() B.4 C.
B.4 C.![]() D.5
D.5
12.已知M点为椭圆上一点,椭圆两焦点为F1,F2,且![]() ,点I为
,点I为![]() 的内心,延长MI交线段F1F2于一点N,则
的内心,延长MI交线段F1F2于一点N,则![]() 的值为
的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:(本大题共4小题,每小题4分,共16分。)
13![]() 已知
已知![]() 满足
满足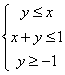 ,则
,则![]() 的最大值为
的最大值为
14![]() 四面体
四面体![]() 中,
中,![]() 是
是![]() 中点,
中点,![]() 是
是![]() 中点,
中点,![]() ,则直线
,则直线![]() 与
与![]() 所成的角大小为
所成的角大小为
15![]()
![]() 的展开式的二项式系数之和为64,则展开式中常数项为
的展开式的二项式系数之和为64,则展开式中常数项为
16.若M是直线![]() 上到原点的距离最近的点,则当
上到原点的距离最近的点,则当![]() 在实数范围内变化时, 动点M的轨迹方程是
在实数范围内变化时, 动点M的轨迹方程是
三、解答题:(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)
17![]() (本小题12分) 已知函数
(本小题12分) 已知函数![]()
![]()
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)当![]() 时,求函数
时,求函数![]() 的最大值,最小值
的最大值,最小值
18![]() (本小题12分)
(本小题12分)
某商场举行抽奖促销活动,抽奖规则是:从装有9个白球、1个红球的箱子中每次随机地摸出一个球,记下颜色后放回,摸出一个红球获得二等奖;摸出两个红球获得一等奖.现有甲、乙两位顾客,规定:甲摸一次,乙摸两次.求
(1)甲、乙两人都没有中奖的概率;
(2)甲、乙两人中至少有一人获二等奖的概率.
19![]() (本小题满分12分)
(本小题满分12分)
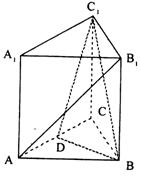
如图,已知正三棱柱ABC- ![]() ,D是AC的中点,∠
,D是AC的中点,∠![]() DC = 60°
DC = 60°
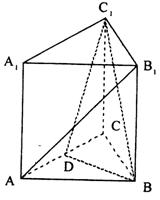 (1)求证:A
(1)求证:A![]() ∥平面B
∥平面B![]() D;
D;
(2)求二面角D-B![]() -C的大小
-C的大小
20![]() (本小题12分)
(本小题12分)
已知函数f(x)=x3+ax2+bx+c在x=-![]() 与x=1时都取得极值.
与x=1时都取得极值.
(1)求a、b的值及函数f(x)的单调区间;
(2)若对x∈[-1,2],不等式f(x)<c2恒成立,求c的取值范围.
21.(本小题12分)
已知数列![]() 中的相邻两项
中的相邻两项![]() 是关于
是关于![]() 的方程
的方程![]() 的两个根,且
的两个根,且![]() .
.
(1)求![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)求数列![]() 的前
的前![]() 项的和
项的和![]() ;
;
(3)求![]()
22![]() (本小题14分)
(本小题14分)
如图,在直角坐标系中,O为坐标原点,直线![]() ⊥x轴与点C,
⊥x轴与点C,
![]() ,
,![]() ,动点
,动点![]() 到直线
到直线![]() 的距离是它到点D的距离的2倍
的距离是它到点D的距离的2倍![]()
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点K为点![]() 的轨迹与x轴正半轴的交点,直线
的轨迹与x轴正半轴的交点,直线![]() 交点
交点![]() 的轨迹于
的轨迹于![]() 两点
两点
(![]() 与点K均不重合),且满足
与点K均不重合),且满足![]()
![]() 求直线EF在X轴上的截距;
求直线EF在X轴上的截距;
 (3)在(2)的条件下,动点
(3)在(2)的条件下,动点![]() 满足
满足![]() ,求直线
,求直线![]() 的斜率的取值范围
的斜率的取值范围![]()
答题卷
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题:
13、 14、 15、 16、
三、解答题:
17、
18、
 19、
19、
20、
21、
22、

(注:解答题答题卷的空间自留)
参考答案
一、选择题
1.B 2.D 3.A 4.D 5.C 6.B 7. A 8.A 9.C 10.D
11.C 12.B
二、填空题
13、3 14、![]() 15、-160 16、
15、-160 16、 ![]() ()
()
三、解答题
17、(1)![]() ……… 3分
……… 3分
![]()
![]() 的最小正周期为
的最小正周期为![]()
![]() …………………
5分
…………………
5分
(2)![]() , …………………
7分
, …………………
7分
![]() ………………… 10分
………………… 10分
![]()
![]()
![]() ………………… 11分
………………… 11分
![]() 当
当![]() 时,函数
时,函数![]() 的最大值为1,最小值
的最大值为1,最小值![]()
![]() ……… 12分
……… 12分
18(1)P1=![]() ;
……… 6分
;
……… 6分
(2)方法一:P2=![]()
方法二:P2=![]()
 方法三:P2=1-
方法三:P2=1-![]() ………
12分
………
12分
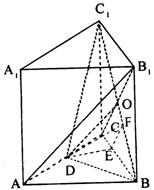
19、解法一:(1)连结![]() C交BC
C交BC![]() 于O,则O是B
于O,则O是B ![]() C的中点,连结DO
C的中点,连结DO
∵在△A![]() C中,O、D均为中点,
C中,O、D均为中点,
∴A![]() ∥DO…………………………2分
∥DO…………………………2分
∵A![]()
![]() 平面B
平面B![]() D,DO
D,DO![]() 平面B
平面B![]() D,∴A
D,∴A![]() ∥平面B
∥平面B![]() D ……4分
D ……4分
(2)设正三棱柱底面边长为2,则DC = 1,
∵∠![]() DC = 60°,∴C
DC = 60°,∴C![]() =
= ![]() ,作DE⊥BC于E。
,作DE⊥BC于E。
∵平面BC![]() ⊥平面ABC,∴DE⊥平面BC
⊥平面ABC,∴DE⊥平面BC![]()
![]()
作EF⊥B![]() 于F,连结DF,则 DF⊥B
于F,连结DF,则 DF⊥B![]()
∴∠DFE是二面角D-B![]() -C的平面角……8分
-C的平面角……8分
在Rt△DEC中,DE=![]()
在Rt△BFE中,EF = BE·sin![]()
∴在Rt△DEF中,tan∠DFE = ![]()
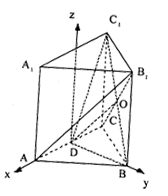 ∴二面角D-B
∴二面角D-B![]() -C的大小为arctan
-C的大小为arctan![]() ………………12分
………………12分
解法二:以AC的中D为原点建立坐标系,如图,
设 AD
= 1∵∠![]() DC =60°∴ C
DC =60°∴ C![]() =
= ![]() ,
,
则A(1,0,0),B(0,![]() ,0),C(-1,0,0),
,0),C(-1,0,0),
![]() (1,0
(1,0![]() ),
),![]() ,
,![]()
(1)连结![]() C交B
C交B![]() 于O是
于O是![]() C的中点,连结DO,则
C的中点,连结DO,则
O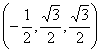 ,
, ![]() =
=![]()
∵A![]()
![]() 平面B
平面B![]() D,∴A
D,∴A![]() ∥平面B
∥平面B![]() D .………………………4分
D .………………………4分
(2)![]() =(-1,0,
=(-1,0,![]() ),
),![]()
设平面B![]() D的法向量为n = ( x , y , z ),则
D的法向量为n = ( x , y , z ),则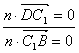
即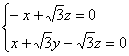 则有
则有![]() = 0令z = 1
= 0令z = 1
则n = (![]() ,0,1)
…………………………………8分
,0,1)
…………………………………8分
设平面BC![]()
![]() 的法向量为m = ( x′ ,y′,z′)
的法向量为m = ( x′ ,y′,z′)
| |
|
|
|
|
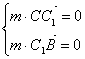 即
即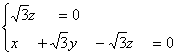 ∴z′= 0
∴z′= 0
![]() 令y = -1,解得m = (
令y = -1,解得m = (![]() ,-1,0)
,-1,0)
二面角D —B![]() —C的余弦值为cos<n , m>=
—C的余弦值为cos<n , m>=
∴二面角D—B![]() —C的大小为arc cos
—C的大小为arc cos![]() …………12分
…………12分
20、(1)f(x)=x3+ax2+bx+c, f′(x)=3x2+2ax+b,
由f′(-![]() )=
)=![]() a+b=0, f′(1)=3+2a+b=0,得
a+b=0, f′(1)=3+2a+b=0,得
a=-![]() ,b=-2,………… 3分
,b=-2,………… 3分![]()
f′(x)=3x2-x-2=(3x+2)(x-1),函数f(x)的单调区间如下表:
| x | (-∞,- | - | (- | 1 | (1,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以函数f(x)的递增区间为(-∞,-![]() )与(1,+∞);递减区间为(-
)与(1,+∞);递减区间为(-![]() ,1)…6分
,1)…6分
(2)f(x)=x3-![]() x2-2x+c
x∈[-1,2],当x=-
x2-2x+c
x∈[-1,2],当x=-![]() 时,f(x)=
时,f(x)=![]() +c为极大值,
+c为极大值,
而f(2)=2+c,则f(2)=2+c为最大值. ………… 8分![]()
要使f(x)<c2(x∈[-1,2])恒成立,只须c2>f(2)=2+c,
解得c<-1或c>2. ………… 12分![]()
21、(1)方程![]() 的两个根为
的两个根为![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() ;当
;当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() 时;
时;
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() .
………… 4分
.
………… 4分![]()
(2)![]()
![]()
![]() .
………… 8分
.
………… 8分![]()
(3)![]() =
=![]() ………… 12分
………… 12分![]()
22、(1)依题意知,点![]() 的轨迹是以点
的轨迹是以点![]() 为焦点、直线
为焦点、直线![]() 为其相应准线,
为其相应准线,
离心率为![]() 的椭圆
的椭圆
设椭圆的长轴长为2a,短轴长为2b,焦距为2c,
又![]() ,
,![]() ,∴点
,∴点![]() 在x轴上,且
在x轴上,且![]() ,且
,且![]() 则
则![]() 3
3
解之得:![]() ,
,![]() ,∴坐标原点
,∴坐标原点![]() 为椭圆的对称中心
为椭圆的对称中心![]()
∴动点M的轨迹方程为:![]()
![]() ………… 4分
………… 4分
(2)设![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() 得
得
![]()
![]() …………
5分
…………
5分
![]() ,
,![]()
![]()
![]() …………
6分
…………
6分
![]()
![]() ,
,![]() ,
,
![]() ,
,![]()
![]()
解得:![]()
![]() (舍)
(舍)![]() ∴ 直线EF在X轴上的截距为
∴ 直线EF在X轴上的截距为 ![]() …………8分
…………8分
(3)设![]() ,由
,由![]() 知,
知,![]()
![]()
直线![]() 的斜率为
的斜率为![]()
![]() ………… 10分
………… 10分
当![]() 时,
时,![]() ;
;
当![]() 时,
时,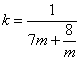 ,
,
![]() 时取“=”)或
时取“=”)或![]() 时取“=”),
时取“=”),
![]() ………… 12分
………… 12分
综上所述 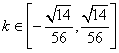 …………
14分
…………
14分![]()