08届高考理科数学第三次模拟考试
数学(理科)
一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
1![]() 计算
计算![]() =
=
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2![]() 过点
过点![]() 的直线
的直线![]() 经过圆
经过圆![]() 的圆心,则直线
的圆心,则直线![]() 的倾斜角大小为
的倾斜角大小为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3![]() 设函数f( x )的图象关于点(1,
设函数f( x )的图象关于点(1,![]() )对称,且存在反函数
)对称,且存在反函数![]() ( x ),若f(3) = 0,
( x ),若f(3) = 0,
则![]() (3)等于
(3)等于
(A)-1 (B)1 (C)-2 (D)2
4![]() 设m,n是两条不同的直线,α、β、γ是三个不同的平面
设m,n是两条不同的直线,α、β、γ是三个不同的平面![]() 给出下列四个命题:
给出下列四个命题:
①若m⊥α,n∥α,则m⊥n; ②若α⊥γ,β⊥γ,则α∥β;
③若m∥α,n∥α,则m∥n; ④若α∥β,β∥γ,m⊥α,,则m⊥γ![]()
其中正确命题的序号是:
(A)①和② (B)②和③ (C)③和④ (D)①和④
5.已知一个正四棱锥的各棱长均相等,则其相邻两侧面所成的二面角的大小为
(A)arcos![]() (B)arcsin(-
(B)arcsin(-![]() )
(C)arctan(
)
(C)arctan(![]() )
(D)arccot(
)
(D)arccot(![]() )
)
6![]()
![]() ,则“
,则“![]() ”是“
”是“![]() ”的
”的
(A)充分非必要条件 (B)必要非充分条件
(C)充分必要条件 (D)既非充分也非必要条件
7![]() 若点
若点![]() 在双曲线
在双曲线![]() 的左准线上,过点
的左准线上,过点![]() 且方向向量为
且方向向量为![]() 的光线,经直线
的光线,经直线![]() 反射后通过双曲线的左焦点,则这个双曲线的离心率为
反射后通过双曲线的左焦点,则这个双曲线的离心率为
 (A)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
8.已知四面体![]() 中,
中,![]() 与
与![]() 间的距离与
间的距离与
夹角分别为3与![]() ,则四面体
,则四面体![]() 的体积为
的体积为
(A)![]() (B)1 (C)2 (D)
(B)1 (C)2 (D)![]()
9.从1,2,3,4,5 中取三个不同数字作直线![]() 中
中![]() 的值,使直线与圆
的值,使直线与圆![]() 的位置关系满足相离,这样的直线最多有
的位置关系满足相离,这样的直线最多有
(A)30条 (B)20条 (C)18条 (D)12条
10.已知等差数列{an}与等差数列{bn}的前n项和分别为Sn和Tn,若![]() ,则
,则![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
11.若![]() ,则方程
,则方程![]() 在(0,2)上恰有( )个实根.
在(0,2)上恰有( )个实根.
(A)0 (B)1 (C)2 (D)3
12.已知M点为椭圆上一点,椭圆两焦点为F1,F2,且![]() ,点I为
,点I为![]() 的内心,延长MI交线段F1F2于一点N,则
的内心,延长MI交线段F1F2于一点N,则![]() 的值为
的值为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
![]()
二、填空题:(本大题共4小题,每小题4分,共16分。)
13![]() 已知
已知![]() 满足
满足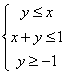 ,则
,则![]() 的最大值为
的最大值为
![]()
14![]()
![]() 的展开式的二项式系数之和为64,则展开式中常数项为
的展开式的二项式系数之和为64,则展开式中常数项为
![]()
15![]() 已知定义在正实数集上的连续函数
已知定义在正实数集上的连续函数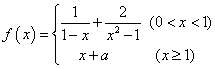 ,则实数
,则实数![]() 的值为
的值为
![]()
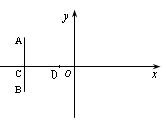
16.若函数f(x)=![]() 在(0,3)上单调递增,则a∈
。
在(0,3)上单调递增,则a∈
。
三、解答题:(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤。)
17![]() (本小题12分)
(本小题12分)
已知函数![]()
![]()
(I)求函数![]() 的最小正周期;
的最小正周期;
(II) 当![]() 时,求函数
时,求函数![]() 的最大值,最小值
的最大值,最小值![]()
18![]() (本小题12分)
(本小题12分)
一厂家向用户提供的一箱产品共10件,其中有2件次品,用户先对产品进行不放回抽检以决定是否接收![]() 抽检规则是这样的:一次取一件产品检查,若前三次没有抽查到次品,则用户接收这箱产品,而前三次中只要抽查到次品就停止抽检,并且用户拒绝接收这箱产品
抽检规则是这样的:一次取一件产品检查,若前三次没有抽查到次品,则用户接收这箱产品,而前三次中只要抽查到次品就停止抽检,并且用户拒绝接收这箱产品![]()
(I)求这箱产品被用户拒绝接收的概率;
(II)记x表示抽检的产品件数,求x的概率分布列及期望![]()
19![]() (本小题满分12分)
(本小题满分12分)
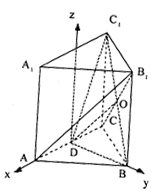
如图,已知正三棱柱ABC- ![]() ,D是AC的中点,∠
,D是AC的中点,∠![]() DC = 60°
DC = 60°
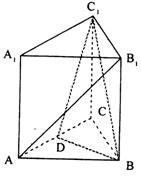 (Ⅰ)求证:A
(Ⅰ)求证:A![]() ∥平面B
∥平面B![]() D;
D;
(Ⅱ)求二面角D-B![]() -C的大小。
-C的大小。
20![]() (本小题12分)
(本小题12分)
已知函数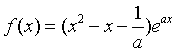 (
(![]() )
)![]()
(Ⅰ) 当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ) 若不等式![]() 对
对![]() 恒成立,求a的取值范围
恒成立,求a的取值范围![]()
21![]() (本小题12分)
(本小题12分)
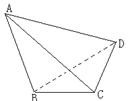
如图,在直角坐标系中,O为坐标原点,直线![]() ⊥x轴于点C,
⊥x轴于点C, ![]() ,
,![]() ,动点
,动点![]() 到直线
到直线![]() 的距离是它到点D的距离的2倍
的距离是它到点D的距离的2倍![]()
(I)求点![]() 的轨迹方程;
的轨迹方程;
(II)设点K为点![]() 的轨迹与x轴正半轴的交点,直线
的轨迹与x轴正半轴的交点,直线![]() 交点
交点![]() 的轨迹于
的轨迹于![]() 两点(
两点(![]() 与点K均不重合),且满足
与点K均不重合),且满足![]()
![]() 求直线EF在X轴上的截距;
求直线EF在X轴上的截距;
(Ⅲ)在(II)的条件下,动点![]() 满足
满足![]() ,求直线
,求直线![]() 的斜率的取值范围
的斜率的取值范围![]()
22.(本小题14分)已知数列![]() 中的相邻两项
中的相邻两项![]() 是关于
是关于![]() 的方程
的方程![]() 的两个根,且
的两个根,且![]() .
.
(I)求![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(II)求数列![]() 的前
的前![]() 项的和
项的和![]() ;
;
(Ⅲ)记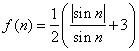 ,
,
![]() ,
,
求证:![]() .
.
2008届高三数学(理科)模拟试题(三)答题卷
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题:
13、 14、 15、 16、
三、解答题:
17、
18、
 19、
19、
20、
21、

22、
高三数学(理科)模拟试题(三)参考答案
一、1 B 2 D 3 A 4 D 5 D 6 B
7 A 8 A 9 C 10 D 11 B 12 B
二、13、3 14、-160 15、![]() 16、
16、![]()
三、17、解: (1)![]()
![]() …… 3分
…… 3分
![]()
![]() 的最小正周期为
的最小正周期为![]()
![]() ………………… 5分
………………… 5分
(2) ![]() ,
………………… 7分
,
………………… 7分
![]() ………………… 10分
………………… 10分
![]()
![]()
![]() ………………… 11分
………………… 11分
![]() 当
当![]() 时,函数
时,函数![]() 的最大值为1,最小值
的最大值为1,最小值![]()
![]() ………… 12分
………… 12分
18、(I)解:设这箱产品被用户拒绝接收事件为A,被接收为![]() ,则由对立事件概率公式
,则由对立事件概率公式
![]() 得:
得:![]()
即这箱产品被用户拒绝接收的概率为![]()
![]() …………
6分
…………
6分
(II)![]()
 ………… 10分
………… 10分
|
| 1 | 2 | 3 |
| P |
|
|
|
…………11分
∴ E![]() =
=![]() …………12分
…………12分
19、解法一:
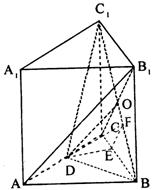 (Ⅰ)连结B1C交BC
(Ⅰ)连结B1C交BC![]() 于O,则O是B
于O,则O是B![]() C的中点,连结DO。
C的中点,连结DO。
∵在△A![]() C中,O、D均为中点,
C中,O、D均为中点,
∴A![]() ∥DO …………………………2分
∥DO …………………………2分
∵A![]()
![]() 平面B
平面B![]() D,DO
D,DO![]() 平面B
平面B![]() D,
D,
∴A![]() ∥平面B
∥平面B![]() D。…………………4分
D。…………………4分
(Ⅱ)设正三棱柱底面边长为2,则DC = 1。
∵∠![]() DC = 60°,∴C
DC = 60°,∴C![]() =
= ![]() 。
。
作DE⊥BC于E。
∵平面BC![]() ⊥平面ABC,
⊥平面ABC,
∴DE⊥平面BC![]()
![]()
作EF⊥B![]() 于F,连结DF,则 DF⊥B
于F,连结DF,则 DF⊥B![]()
∴∠DFE是二面角D-B![]() -C的平面角……………………………………8分
-C的平面角……………………………………8分
在Rt△DEC中,DE=![]()
在Rt△BFE中,EF = BE·sin![]()
∴在Rt△DEF中,tan∠DFE = ![]()
 ∴二面角D-B
∴二面角D-B![]() -C的大小为arctan
-C的大小为arctan![]() ………………12分
………………12分
解法二:以AC的中D为原点建立坐标系,如图,
设 AD = 1∵∠![]() DC =60°∴ C
DC =60°∴ C![]() =
= ![]() 。
。
则A(1,0,0),B(0,![]() ,0),C(-1,0,0),
,0),C(-1,0,0),
![]() (1,0
(1,0![]() ),
),![]() ,
,![]()
(Ⅰ)连结![]() C交B
C交B![]() 于O是
于O是![]() C的中点,连结DO,则
O
C的中点,连结DO,则
O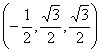 .
. ![]() =
=![]()
∵A![]()
![]() 平面B
平面B![]() D,
D,
∴A![]() ∥平面B
∥平面B![]() D.……………………………………………………………4分
D.……………………………………………………………4分
(Ⅱ)![]() =(-1,0,
=(-1,0,![]() ),
),![]()
设平面B![]() D的法向量为n = ( x , y , z ),则
D的法向量为n = ( x , y , z ),则![]()
即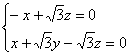 则有
则有![]() = 0令z = 1
= 0令z = 1
则n = (![]() ,0,1)…………………………………………………………8分
,0,1)…………………………………………………………8分
设平面BC![]()
![]() 的法向量为m = (
x′ ,y′,z′)
的法向量为m = (
x′ ,y′,z′)
| |
|
|
|
|
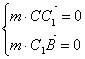 即
即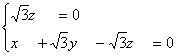 ∴z′= 0
∴z′= 0
![]() 令y = -1,解得m = (
令y = -1,解得m = (![]() ,-1,0)
,-1,0)
二面角D —B![]() —C的余弦值为cos<n , m>=
—C的余弦值为cos<n , m>=
∴二面角D—B![]() —C的大小为arc cos
—C的大小为arc cos![]() …………12分
…………12分
20、解: 对函数![]() 求导得:
求导得:![]() ……………2分
……………2分
(Ⅰ)当![]() 时,
时, ![]()
令![]() 解得
解得 ![]() 或
或![]()
![]() 解得
解得![]()
所以, ![]() 单调增区间为
单调增区间为![]() ,
,![]() ,
,
![]() 单调减区间为(-1,1)
……………5分
单调减区间为(-1,1)
……………5分
(Ⅱ) 令![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ………… 6分
………… 6分
由![]() 时,列表得:
时,列表得:
| x |
|
|
| 1 |
|
|
| + | 0 | - | 0 | + |
|
|
| 极大值 |
| 极小值 |
|
……………8分
对于![]() 时,因为
时,因为![]() ,所以
,所以![]() ,
,
∴![]() >0
…………
10 分
>0
…………
10 分
对于![]() 时,由表可知函数在
时,由表可知函数在![]() 时取得最小值
时取得最小值![]()
所以,当![]() 时,
时,![]()
由题意,不等式![]() 对
对![]() 恒成立,
恒成立,
所以得![]() ,解得
,解得![]() ……………12分
……………12分
21、解: (I)依题意知,点![]() 的轨迹是以点
的轨迹是以点![]() 为焦点、直线
为焦点、直线![]() 为其相应准线,
为其相应准线,
离心率为![]() 的椭圆
的椭圆
设椭圆的长轴长为2a,短轴长为2b,焦距为2c,
又![]() ,
,![]() ,∴点
,∴点![]() 在x轴上,且
在x轴上,且![]() ,则
,则![]() 3,
3,![]()
解之得:![]() ,
,![]()
![]()
∴坐标原点![]() 为椭圆的对称中心
为椭圆的对称中心![]()
∴动点M的轨迹方程为:![]()
![]() ………… 4分
………… 4分
(II)设![]() ,设直线
,设直线![]() 的方程为
的方程为![]() (-2〈n〈2),代入
(-2〈n〈2),代入![]() 得
得
![]()
![]() ………… 5分
………… 5分
![]() ,
,![]()
![]()
![]() ………… 6分
………… 6分
![]()
![]() ,K(2,0),
,K(2,0),![]() ,
,
![]() ,
,
![]()
![]()
解得:![]()
![]() (舍)
(舍)![]() ∴ 直线EF在X轴上的截距为
∴ 直线EF在X轴上的截距为
![]() …………8分
…………8分
(Ⅲ)设![]() ,由
,由![]() 知,
知,![]()
![]()
直线![]() 的斜率为
的斜率为![]()
![]() ………… 10分
………… 10分
当![]() 时,
时,![]() ;
;
当![]() 时,
时,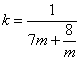 ,
,
![]() 时取“=”)或
时取“=”)或![]() 时取“=”),
时取“=”),
![]()
综上所述 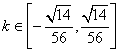 ………… 12分
………… 12分![]()
22、(I)解:方程![]() 的两个根为
的两个根为![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() 时;
时;
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() . ………… 4分
. ………… 4分![]()
(II)解:![]()
![]()
![]() .
…………
8分
.
…………
8分![]()
(III)证明:![]() ,
,
所以![]() ,
,
![]() .
…………
9分
.
…………
9分![]()
当![]() 时,
时,
![]() ,
,
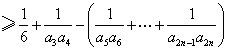
![]()
![]() …………
11分
…………
11分![]()
同时,![]()
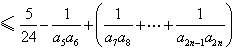
![]()
![]() .
…………
13分
.
…………
13分![]()
综上,当![]() 时,
时,![]() .
…………
14分
.
…………
14分![]()