08届高中毕业班理科数学第三次质量检查
数学试题（理科）
考试时间：120分钟 试卷满分：150分
注意事项：
准考证号码填写说明：准考证号码共九位，每位都体现不同的分类，具体如下：
| 0 | 5 | 0 | 0 | 0 |
答题卡上科目栏内必须填涂考试科目
一、选择题：（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的，）
1．已知全集为
，则有 （ ）
A．
B．
C．
D．
2．已知
为第三象限角，则
的值 （ ）
A．一定为正数 B．一定为负数
C．可能为正数，也可能为负数 D．不存在
3．若
，则下列不等式成立的是
A．
B．
C．
D．
4．在△ABC中，已知三边满足：(a+b+c)(a+b-c)=3ab,则角C等于 （ ）
A．150° B．30° C．45° D．60°
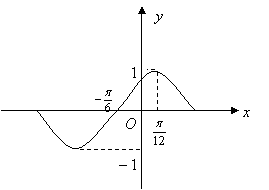5．下列函数中，图象的一部分如图所示的是（ ）
A．
B．
C．
D．
6．若数列{an}由a1=2,an+1=an+2n(n
)确定，则a100的值为 （ ）
A．9900 B．9902 C．9904 D．9906
7．如果－1，a，b，c，－9成等比数列，那么 （ ）
A．b=3,ac=9 B．b=3,ac=－9 C．b=－3,ac=9 D．b=－3,ac=－9
8．已知函数
的图象经过点
,则该函数的一条对称轴方程为
（ ）
A．
B．
C．
D．
9．已知一个等差数列的前９项的算术平均数为10,前10项的算术平均数为11,则此等差数列的公差为 （ ）
A．1 B．2 C．
D．4
|
，点P在向量
的延长线上，且
则点P的坐标 （ ）
A．（－2，11） B．
C．
D．（－1，8）
11．如果
，那么
的取值范围是 （ ）
A．
，
B．，
C．，
，
D．，
，
12．若
是等差数列，
是其前
项和，
，
，则
，
，
，…，中最小的是 （ ）
A．
B．
C．
D．
二、填空题：(本大题共有4个小题，每小题4分，共计16分.)
13．已知向量
，且A、B、C三点共线，则k=
14．已知
，
，
，则
15．不等式
＜1的解集为{xx＜1或x＞2＝,那么a的值为____________
16．有穷数列
，是其前项和，定义数列的凯森和为
。若有99项的数列
的凯森和为1000，则有100项的1，的凯森和为___________
三、解答题:( 本大题共有6个小题，共74分。解答应写出文字说明、演算步骤或证明过程。)
|
已知A（3，0），B（0，3），C（cos
,sin）.
（1）若
的值。
（2）O为坐标原点，若
。
18．（本小题满分12分）
已知函数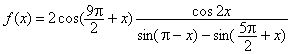
（1）求函数
的最小正周期、
单调递减区间；
（2）的图象由y=sinx的图
象经过怎样的变换可以得到；
（3）在给出的直角坐标系中，画
出函数
在区间
上的图象.
19．（本小题满分12分）
设Sn是数列的前n项和，所有项
, 且
，
（1）求数列的通项公式.
（2）
的值.
20．（本小题满分12分）
某外商到一开放区投资72万美元建起一座蔬菜加工厂，第一年各种经费12万美元，以后每年增加4万美元，每年销售蔬菜收入50万美元.设
表示前n年的纯收入（=前n年的总收入－前n前的总支出－投资额）
（1）从第几年开始获取纯利润？
（2）若干年后，外商为开发新项目，有两种处理方案：①年平均利润最大时以48万美元出售该厂；②纯利润总和最大时，以16万美元出售该厂，问哪种方案更合算？
21．（本小题满分12分）
设函数
的图象关于原点对称，
的图象在点
（1，
）处的切线的斜率为-6，且当
时有极值.
（1）求
的值；
（2）若
，求证：
.
22．（本小题满分14分）
设函数f(x)=3x2+1,g(x)=2x，现有数列{
}满足条件：对于n∈
, ＞0且f(+1)-f()=g(
+),又设数列{
}满足条件：=
(
，
n∈).
（1）求证：数列{}为等比数列；
（2）求证:数列
是等差数列；
（3）设k,L∈*,且k+L=5,
=
,
=
，求数列{}的通项公式；
（4）如果k+L=M0(k,L∈N+,M0＞3且M0是奇数)，且=,=,求从第几项
开始＞1恒成立.
参考答案
一、选择题：
|
二、填空题：
13．
14．
15．
16．991
三、解答题:( 本大题共有6个小题，共74分。解答应写出文字说明、演算步骤或证明过程。)
17．解：
18．解：（1）
………………………1分
………………2分
所以函数的最小正周期为π.………………………3分
所以函数的单调递减区间为
……………5分
（2）
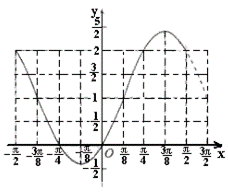
………9分
（3）由（1）知
|
|
|
|
|
|
|
|
| 1 |
| 1 |
| 1 |
故函数
在区间
上
的图象是 ……………………12分
19．解：（1）当n = 1时，
解得a1 = 3…………2分
当n≥2时，
= 
(an2
+ 2an-1－3)- (
+ 2an－3)………3分
∴4an = an2－ + 2an－2an－1
∴ 
（
）…………5分
是以3为首项，2为公差的等差数列
…………6分
（2）
①
又
②
②－① 
∴
…………12分
20．解：由题意知，每年的经费是以12为首项，4为公差的等差数列，设纯利润与年数的关系为
…2分
（1）纯利润就是要满足
………………4分
解得 
知从第三年开始获利 …………6分
（2）①年平均利润
当且仅当n=6时等号成立.
此方案共获利6×16+48=144（万美元），此时n=6，…………8分
②
当n=10时，
.
故第②种方案共获利128+16=144（万美元），……10分
故比较两种方案，获利都是144万美元。
但第①种方案只需6年，而第②种方案需10年，故选择第①方案更合算.……12分
21．解
(1) 
关于原点对称,
由
对
恒成立有
则
, 又
,
故
……6分
（2）
，
当
时，
，在[-1，1]上递减，而
即
同理，
，故.…………12分
22．解：（1）∵f(x)=3x2+1，g(x)=2x，f(an+1)-f(an)=g(an+1+)
∴3(an+1)2+1-3a2n-1=2(an+1+),即6an=2an+1
∴
=3 ∴数列{an}是以3为公比的等比等列…………3分
（2）∵bn=
∴
=
,
=
∴-=
=
∴数列{}是以
为首项，公差为的等差数列…………6分
（3）为方便起见,记数列{}的公差为
,由于
.
又∵bk=,bL=
∴ 
, ∴
∴
∵k+L=5 ∴
∴
=
…………10分
（4）若k +L =M0，由（3）可知 =
=3M0-3n+1
假设第M+1项开始满足an＞1恒成立，
∵bn=(，n∈N*) ∴
由（3）知
,∴0＜a＜1，所以要an＞1恒成立，只需＜0，即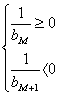
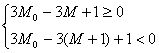
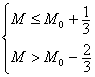
又M∈N*
∴M=M0，即数列{an}从第M0+1项开始以后的项满足a n＞1…14分