08届高考数学二摸模拟试卷
姓名: 班级: 学号:
一、填空题:本大题共14小题,每小题5分,共70分。把答案填在横线上。
1、已知集合![]() ,
,![]() 。若
。若![]() ,则实数
,则实数![]() 的取值范围是____________。
的取值范围是____________。
2、已知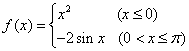 ,若
,若![]() ,则
,则![]() 。
。
3、已知直线![]() ,直线
,直线![]() 与
与![]() 关于直线
关于直线![]() 对称,则直线
对称,则直线![]() 的斜率为 。
的斜率为 。
4、方程![]() 有实根的概率为
。
有实根的概率为
。
5、三角形ABC中AP为BC边上的中线,![]() ,
,![]() ,则
,则![]() = 。
= 。
6、已知函数![]() ,若方程
,若方程![]() 有三个不同的根,且从小到大
有三个不同的根,且从小到大
依次成等比数列,则![]() 的值为 。
的值为 。
7、对任意实数![]() ,定义运算
,定义运算![]() ,其中
,其中![]() 是常数,等式右边的运算是通常的加法和乘法运算。已知
是常数,等式右边的运算是通常的加法和乘法运算。已知![]() ,并且有一个非零常数
,并且有一个非零常数![]() ,使得对任意实数
,使得对任意实数![]() ,都有
,都有![]() ,则
,则![]() 的值是 。
的值是 。
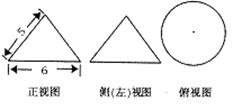
8、一个几何体的三视图及其尺寸如下左图(单位:㎝),则该几何体的表面积是 ,
|
 体积是
。
体积是
。
9、如上右图,在杨辉三角形中,斜线l的上方从1按箭头所示方向可以构成一个“锯齿形”的数列![]() :1,3,3,4,6,5,10,…,则a21的值为
。
:1,3,3,4,6,5,10,…,则a21的值为
。
10、对于在区间![]() 上有意义的两个函数
上有意义的两个函数![]() 和
和![]() ,如果对任意
,如果对任意![]() ,均有
,均有![]() , 那么我们称
, 那么我们称![]() 和
和![]() 在
在![]() 上是接近的。若
上是接近的。若![]() 与
与![]() 在闭区间
在闭区间![]() 上是接近的,则
上是接近的,则![]() 的取值范围是
。
的取值范围是
。
11、已知复数![]() (
(![]() 为虚数单位),且复数
为虚数单位),且复数![]() 在复平面上对应的点在第一象限,则实数
在复平面上对应的点在第一象限,则实数![]() 的取值范围为
。
的取值范围为
。
12、已知数列![]() 满足
满足![]() ,
,![]() ,
,
则![]() 。
。
13、如图,在矩形ABCD中,AB=1,BC=![]() ,此矩形沿地面上一直线滚动,在滚动过程中始终与地面垂直,设直线BC与地面所成角为
,此矩形沿地面上一直线滚动,在滚动过程中始终与地面垂直,设直线BC与地面所成角为![]() ,矩形周边上最高点离地面的距离为
,矩形周边上最高点离地面的距离为

![]() ,则
,则![]() = 。
= 。
14、符号![]() 表示不超过
表示不超过![]() 的最大整数,如
的最大整数,如![]() 。定义函数
。定义函数![]() ,给出如下四个命题:①函数
,给出如下四个命题:①函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ; ②方程
; ②方程![]() 有无数解;
有无数解;
③函数![]() 是周期函数;
④函数
是周期函数;
④函数![]() 是
是![]() 上的增函数。
上的增函数。
其中正确命题的序号是 。
二、解答题:本大题共90分,解答应写出文字说明、证明过程或演算步骤。
15、(本小题满分14分)
已知a、b、c是△ABC三边长,关于x的方程![]() 的两根之差的平方等于4,△ABC的面积
的两根之差的平方等于4,△ABC的面积![]()
(Ⅰ)求角C;
(Ⅱ)求a、b的值.
16、(本小题满分14分)已知![]() 是
是![]() 的三个内角,
的三个内角,![]() 。
。
(1)若![]() 是正三角形,求
是正三角形,求![]() 的值;
的值;
(2)若任意交换![]() 中两个角的位置,
中两个角的位置,![]() 的值是否变化?证明你的结论;
的值是否变化?证明你的结论;
(3)若![]() 中有一内角为
中有一内角为![]() ,求
,求![]() 的最小值。
的最小值。
17、(本小题满分14分)
已知数列{an}的前n项和为Sn,且满足![]()
(Ⅰ)判断![]() 是否为等差数列?并证明你的结论;
是否为等差数列?并证明你的结论;
(Ⅱ)求Sn和an
| |
18、(本小题满分16分)
设![]() 是函数
是函数![]() 的两个极值点,且
的两个极值点,且![]()
(Ⅰ)求a的取值范围;
(Ⅱ)求证:![]() .
.
19、(本小题满分16分)
甲、乙两公司同时开发同一种新产品,经测算,对于函数f(x)、g(x),当甲公司投入x万元作宣传时,若乙公司投入的宣传费小于f(x)万元,则乙公司对这一新产品的开发有失败的风险,否则没有失败的风险;当乙公司投入x万元作宣传时,若甲公司投入的宣传费小于g(x)万元,则甲公司对这一新产品的开发有失败的风险,否则没有失败的风险。
(Ⅰ)试解释![]() 的实际意义;
的实际意义;
(Ⅱ)设![]() ,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
20、(本小题满分16分)
椭圆G:![]() 的两个焦点F1(-c,0)、F2(c,0),M是椭圆上的一点,且满足
的两个焦点F1(-c,0)、F2(c,0),M是椭圆上的一点,且满足![]()
(Ⅰ)求离心率e的取值范围;
(Ⅱ)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为![]()
(1)求此时椭圆G的方程;
(2)设斜率为k(k≠0)的直线l与椭圆G相交于不同的两点A、
B,Q为AB的中点,问A、B两点能否关于过点![]() 的直线对称?若能,求出k
的直线对称?若能,求出k
的取值范围;若不能,请说明理由.
参考答案
1、![]() 2、
2、![]() 或
或![]() 3、
3、![]() 4、
4、![]() 5、
5、![]()
6、![]() 7、
7、![]() 8、24
8、24![]() ,12
,12![]() 9、66 10、
9、66 10、![]() 11、
11、![]()
12、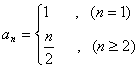 13、
13、![]() 14、②③
14、②③
15、解:(Ⅰ)设![]() 的两根
的两根
则![]()
![]() ……………………………………………………………………2分
……………………………………………………………………2分
![]()
![]() ………………………………………………………………4分
………………………………………………………………4分
又![]()
![]()
![]() ……………………………………………………………………6分
……………………………………………………………………6分
(Ⅱ)由![]()
![]() ①………………………………………………………………8分
①………………………………………………………………8分
由余弦定理:
![]()
即:![]()
![]()
![]() ②……………………………………………………12分
②……………………………………………………12分
由①②得:a=8,b=5 ……………………………………………………14分
16、(1)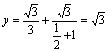 。……………………………………………………………………(3分)
。……………………………………………………………………(3分)
(2)∵![]() , (7分)
, (7分)
∴若任意交换![]() 中两个角的位置,
中两个角的位置,![]() 的值不会改变。……………………………(8分)
的值不会改变。……………………………(8分)
(3)不妨设![]() ,
,
则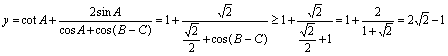 ,…(12分)
,…(12分)
当且仅当![]() 时,
时,![]() 。……………………………………………(14分)
。……………………………………………(14分)
17、解证:(Ⅰ)![]() ………………………………1分
………………………………1分
当n≥2时,![]() ………………2分
………………2分
![]()
故![]() 是以2为首项,以2为公差的等差数列.…………………………4分
是以2为首项,以2为公差的等差数列.…………………………4分
(Ⅱ)由(Ⅰ)得![]() …………………5分
…………………5分
当n≥2时,![]() …………………………6分
…………………………6分
当n=1时,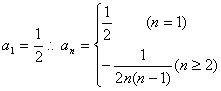 ………………8分
………………8分
(Ⅲ)1°当n=1时,![]() 成立…………………………9分
成立…………………………9分
2°假设n=k时,不等式成立,即![]() 成立
成立
则当n=k+1时,![]()
![]()
![]()
即当n=k+1时,不等式成立
由1°,2°可知对任意n∈N*不等式成立.
(Ⅲ)另证:![]()
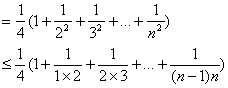
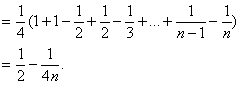 …………14分
…………14分
18、解证:(I)易得![]() …………………………………………1分
…………………………………………1分
![]() 的两个极值点
的两个极值点
![]() 的两个实根,又a>0
的两个实根,又a>0
![]() ……………………………………………………5分
……………………………………………………5分
∴![]()
∵![]()
![]()
![]() ……………………………………………………9分
……………………………………………………9分
(Ⅱ)设![]() 则
则
![]()
由![]()
![]() 上单调递增………………12分
上单调递增………………12分
![]()
![]() ………………………………………………16分
………………………………………………16分
19、解:(I)f(0)=10表示当甲公司不投入宣传费时,乙公司要避免新产品的开发有失败风险,至少要投入10万元宣传费;g(0)=20表示当乙公司不投入宣传费时,甲公司要避免新产品的开发有失败的风险,至少要投入20万元宣传费。…………………………4分
(Ⅱ)设甲公司投入宣传费x万元,乙公司投入宣传费y万元,依题意,当且仅当
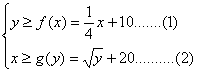 成立,双方均无失败的风险……………………8分
成立,双方均无失败的风险……………………8分
由(1)(2)得![]()
![]()
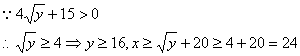 ……………………14分
……………………14分
![]()
答:要使双方均无失败风险,甲公司至少要投入24万元,乙公司至少要投入16万元。
……………………………………………………………………………………16元
20解:(I)设M(x0,y0)
![]() ①
①
又![]() ②……………………2分
②……………………2分
由②得![]() 代入①式整理得
代入①式整理得 ![]()
又![]()
解得![]()
![]() ……………………………………………………………………4分
……………………………………………………………………4分
(Ⅱ)(i)当![]()
设H(x,y)为椭圆上一点,则
![]()
若0![]()
由![]() (舍去)…………………………6分
(舍去)…………………………6分
若b≥3,当y=-3时,HN2有最大值2b2+18
由2b2+18=50得b2=16
∴所求椭圆方程为![]() ……………………………………8分
……………………………………8分
(ii)设A(x1,y1),B(x2,y2),Q(x0,y0),则由
 ③
③
又直线PQ⊥直线l ∴直线PQ方程为![]()
将点Q(x0,y0)代入上式得,![]() ④………………11分
④………………11分
由③④得Q![]() …………………………………………12分
…………………………………………12分
(解1)而Q点必在椭圆内部 ![]()
由此得![]()
![]()
故当![]() 时A、B两点关于点P、Q的直线对称.…………16分
时A、B两点关于点P、Q的直线对称.…………16分
(解2)∴AB所在直线方程为![]()
由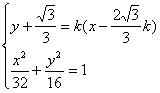 得
得
![]()
显然1+2k2≠0
而![]()
![]()
直线l与椭圆有两不同的交点A、B ∴△>0
解得![]()
![]()
故当![]() 时,A、B两点关于点P、Q的直线对称。
时,A、B两点关于点P、Q的直线对称。
…………………………………………………………………………16分
(ii)另解;设直线l的方程为y=kx+b
由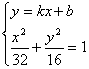 得
得
![]()
设A(x1,y1),B(x2,y2),Q(x0,y0),则
![]() ③……………………9分
③……………………9分
又直线PQ⊥直线l ∴直线PQ方程为![]()
将点Q(x0,y0)代入上式得,![]() ④………………10分
④………………10分
将③代入④![]() ⑤…………………………………………11分
⑤…………………………………………11分
∵x1,x2是(*)的两根
![]() ⑥……12分
⑥……12分
⑤代入⑥得![]()
∴当![]() 时,A、B两点关于点P、Q的直线对称。……16分
时,A、B两点关于点P、Q的直线对称。……16分