08届高考数学典型问题与易错问题
典型问题
1.在△ABC中,a、b、c分别为角A、B、C的对边,![]() ,则△ABC的形状为( B )
,则△ABC的形状为( B )
A.正三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
2.“![]() ”是“
”是“![]() ”的 条件。(答:充分非必要条件)
”的 条件。(答:充分非必要条件)
3.已知平面上三点A、B、C满足![]() 的值等于 ( C )
的值等于 ( C )
A.25 B.
4.函数![]() 的图象按向量
的图象按向量![]() 平移后,所得函数的解析式是
平移后,所得函数的解析式是![]() ,则
,则![]() =________(答:
=________(答:![]() )
)
5、已知两圆方程分别为:![]() ,
,![]() ,则两圆的公切线方程为(A)
,则两圆的公切线方程为(A)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、已知动点![]() 满足
满足![]() ,
,![]() 为坐标原点,则
为坐标原点,则![]() 的取值范围是_
的取值范围是_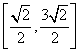 ______
______
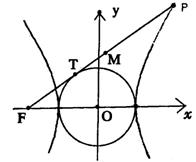
16、对正整数![]() ,设抛物线
,设抛物线![]() ,过
,过![]() 任作直线
任作直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,则数列
两点,则数列![]() 的前
的前![]() 项和为__—n(n+1)________
项和为__—n(n+1)________
7.正实数x1,x2及函数,f
(x)满足![]() ,则
,则![]() 的最小值为 ( B )
的最小值为 ( B )
A.4 B.![]() C.2 D.
C.2 D.![]()
8.已知函数![]() ,则“b >
,则“b >
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
9.椭圆![]() 与直线
与直线![]() 交于A、B两点,过原点与线段AB中点的直线的斜率为
交于A、B两点,过原点与线段AB中点的直线的斜率为![]() 的值为 ( A )
的值为 ( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知:![]() 是直线,
是直线,![]() 是平面,给出下列四个命题:(1)若
是平面,给出下列四个命题:(1)若![]() 垂直于
垂直于![]() 内的两条直线,则
内的两条直线,则![]() ;(2)若
;(2)若![]() ,则
,则![]() 平行于
平行于![]() 内的所有直线;(3)若
内的所有直线;(3)若![]() 且
且![]() 则
则![]() ;(4)若
;(4)若![]() 且
且![]() 则
则![]() ;(5)若
;(5)若![]() 且
且![]() 则
则![]()
![]() 。其中正确命题的个数是
( B )
。其中正确命题的个数是
( B )
(A) 0 (B) 1 (C) 2 (D) 3
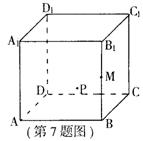
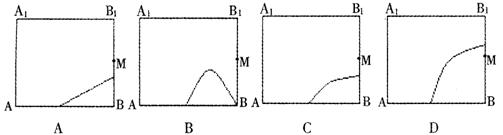
|
有一动点P到平面A
倍,点M是棱BB1的中点,则动点P所在曲线的大致
| |
|
12.一次研究性课堂上,老师给出函数![]() ,三位同学甲、乙、丙在研究此函数时分别给出命题:
,三位同学甲、乙、丙在研究此函数时分别给出命题:
甲:函数f (x)的值域为(-1,1);
乙:若x1≠x2,则一定有f (x1)≠f (x2);
丙:若规定![]() 对任意
对任意![]() 恒成立.
恒成立.
你认为上述三个命题中正确的个数有( D )
A.0个 B.1个 C.2个 D.3个
13.已知函数![]() 在区间
在区间![]() 上是增函数,则
上是增函数,则![]() 的取值范围是____(答:
的取值范围是____(答:![]() ));
));
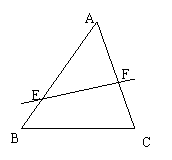
14. 在△ABC中,E、F分别为AB、AC上的点,若![]() =m,
=m,![]() =n,则
=n,则
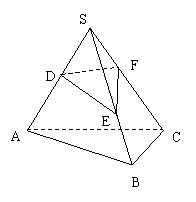
![]() = mn. 拓展到空间:在三棱锥S-ABC中,D、E、F分别是侧棱SA、SB、SC上的点,若
= mn. 拓展到空间:在三棱锥S-ABC中,D、E、F分别是侧棱SA、SB、SC上的点,若![]() = m,
= m,![]() =n,
=n,![]() = p,则
= p,则![]() =
= ![]() .
.
 |
15.已知双曲线![]() 的右焦点为F,右准线与一条渐近线交于点A,
的右焦点为F,右准线与一条渐近线交于点A,
△OAF的面积为![]() (O为坐标原点),则双曲线的两条渐近线的夹角为 60°
(O为坐标原点),则双曲线的两条渐近线的夹角为 60°
16.直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数f (x)的图象恰好通过k个格点,则称函数f (x)为k阶格点函数.下列函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 其中是一阶格点函数的有 ①②④ .(填上所有满足题意的序号)
其中是一阶格点函数的有 ①②④ .(填上所有满足题意的序号)
17.已知△ABC,若对任意t∈R,≥,则C
A.∠A=900 B.∠B=
18.等差数列![]() 的前
的前![]() 项和为
项和为![]() ,公差
,公差![]() . 若存在正整数
. 若存在正整数![]() ,使得
,使得![]() ,则当
,则当![]() (
(![]() )时,有
)时,有![]() (填“>”、“<”、“=”).
(填“>”、“<”、“=”).
![]()
(6)设等差数列{an}的前n项和为Sn,已知S12>0,S13<0,则 ,,…, 中最大的是 B
(A) (B) (C) (D)
19.定义在N*上的函数![]() 满足:f(0) = 2,f(1) = 3,
满足:f(0) = 2,f(1) = 3,
且![]() .
.
(Ⅰ)求f(n)(nÎN*);
(Ⅱ)求![]() .
.
(Ⅰ)由题意:![]() ,所以有:
,所以有:![]() ,又
,又![]() ,所以
,所以![]() ,即
,即![]() ,故
,故![]() .
.
(Ⅱ)![]() .
.
20.已知数列{an}满足a1=1,a2=-13,![]()
(Ⅰ)设![]() 的通项公式;
的通项公式;
(Ⅱ)求n为何值时,![]() 最小(不需要求
最小(不需要求![]() 的最小值)
的最小值)
解:(I)![]()
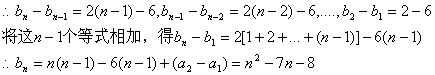
即数列{bn}的通项公式为![]()
(Ⅱ)若an最小,则![]()
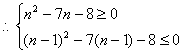 注意n是正整数,解得8≤n≤9
注意n是正整数,解得8≤n≤9
∴当n=8或n=9时,an的值相等并最小
21.已知函数f(x)=x3+ax2+bx+c关于点(1,1)成中心对称,且f '(1)=0.
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)设数列{an}满足条件:a1∈(1,2),an+1=f (an)
求证:(a1- a2)·(a3-1)+(a2- a3)·(a4-1)+…+(an- an+1)·(an+2-1)<1
解:(Ⅰ)由f(x)=x3+ax2+bx+c关于点(1,1)成中心对称,所以
x3+ax2+bx+c+(2-x)3+a(2-x)2+b(2-x)+c=2
对一切实数x恒成立.得:a=-3,b+c=3,
对由f '(1)=0,得b=3,c=0,
故所求的表达式为:f(x)= x3-3x2+3x.
(Ⅱ) an+1=f (an)= an 3-3 an 2+3 an (1)
令bn=an-1,0<bn<1,由代入(1)得:bn+1=![]() ,bn=
,bn=![]() ,
,
∴ 1>bn >bn+1 >0
(a1-a2)·(a3-1)+(a2-a3)·(a4-1)+…+(an-an+1)·(an+2-1)=![]()
<![]() =b1-bn+1<b1<1。
=b1-bn+1<b1<1。
22.设函数![]() .
.
(Ⅰ)如果![]() ,点P
,点P![]() 曲线
曲线![]() 上一个动点,求以P为切点的切线其斜率取最小值时的切线方程;
上一个动点,求以P为切点的切线其斜率取最小值时的切线方程;
(Ⅱ)若![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
.解(Ⅰ)设切线斜率为![]() 则
则![]() 当
当![]() 时
时![]() 最小值为
最小值为![]() .
.![]()
所以切线方程为![]() 即
即![]()
(Ⅱ)由![]() >0
>0 ![]() <0得.
<0得.
函数![]() 在
在![]() 为增函数,在
为增函数,在![]() 减函数
减函数
(1)![]() ,无解; (2)
,无解; (2)![]() 无解;
无解;
(3)![]() ,解得
,解得![]() .综上所述
.综上所述 ![]() .
.
23.已知O为坐标原点,点E、F的坐标分别为(-1,0)、(1,0),动点A、M、N满足![]() (
(![]() ),
),![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求点M的轨迹W的方程;
(Ⅱ)点![]() 在轨迹W上,直线PF交轨迹W于点Q,且
在轨迹W上,直线PF交轨迹W于点Q,且![]() ,若
,若![]() ,求实数
,求实数![]() 的范围.
的范围.
解:(Ⅰ)∵![]() ,
,![]() ,
,
∴ MN垂直平分AF.
又![]() ,∴ 点M在AE上,
,∴ 点M在AE上,
∴ ![]() ,
,![]() ,
,
∴ ![]() ,
,
∴ 点M的轨迹W是以E、F为焦点的椭圆,且半长轴![]() ,半焦距
,半焦距![]() ,
,
∴ ![]() .
.
∴ 点M的轨迹W的方程为![]() (
(![]() ).
).
(Ⅱ)设![]()
∵ ![]() ,
,![]() ,
,
∴ 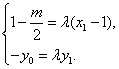 ∴
∴ 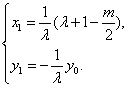
由点P、Q均在椭圆W上,
∴ 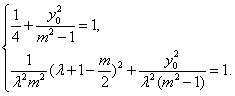
消去![]() 并整理,得
并整理,得![]() ,
,
由![]() 及
及![]() ,解得
,解得![]() .
.
24.已知函数![]() 的定义域为
的定义域为![]() ,导数
,导数![]() 满足0<
满足0<![]() <2
且
<2
且![]() ,常数
,常数![]() 为方程
为方程![]() 的实数根,常数
的实数根,常数![]() 为方程
为方程![]() 的实数根.
的实数根.
(Ⅰ)若对任意![]() ,存在
,存在![]() ,使等式
,使等式![]() 成立.试问:方程
成立.试问:方程![]() 有几个实数根;
有几个实数根;
(Ⅱ)求证:当![]() 时,总有
时,总有![]() 成立;
成立;
(Ⅲ)对任意![]() ,若满足
,若满足![]() ,求证:
,求证:![]() 。
。
21、(I)假设方程![]() 有异于
有异于![]() 的实根m,即
的实根m,即![]() .则有
.则有
![]() 成立
.
成立
.
因为![]() ,所以必有
,所以必有![]() ,但这与
,但这与![]() ≠1矛盾,
≠1矛盾,
因此方程![]() 不存在异于c1的实数根.
不存在异于c1的实数根.
∴方程![]() 只有一个实数根.
只有一个实数根.
(II)令![]() ,
,
∴函数![]() 为减函数.
为减函数.
又![]() ,
,
∴当![]() 时,
时,![]() ,即
,即![]() 成立.
成立.
(III)不妨设![]() ,
,![]() 为增函数,
为增函数,
即![]() .又
.又![]() ,∴函数
,∴函数![]() 为减函数
为减函数
即![]() .
.
![]() ,
,
即![]() .
.
![]() ,
,
![]() .
.
25、平面直角坐标系中,已知![]() 、
、![]() 、
、![]() ,满足向量
,满足向量
![]() 与向量
与向量![]() 共线,且点
共线,且点![]() 都在斜率为6的同一条直线上.
都在斜率为6的同一条直线上.
(1)试用![]() 与n来表示
与n来表示![]() ;
;
(2)设![]() ,且12<a≤15,求数列
,且12<a≤15,求数列![]() 中的最小值的项.
中的最小值的项.
解:(1)![]() 点
点![]() 都在斜率为6的同一条直线上,
都在斜率为6的同一条直线上,
![]()
![]() ,即
,即![]() ,
,
于是数列![]() 是等差数列,故
是等差数列,故![]() .
.
![]()
![]() ,
,![]() ,又
,又![]() 与
与![]() 共线,
共线,
![]()
![]()
![]()
![]()
![]() .
.
当n=1时,上式也成立.
所以an![]() .
.
(2)把![]() 代入上式,
代入上式,
得![]()
![]()
![]()
![]() 12<a≤15,
12<a≤15,![]() ,
,
![]() 当n=4时,
当n=4时,![]() 取最小值,
取最小值,![]() 最小值为a4=18-
最小值为a4=18-
26.已知二次函数![]() 为偶函数,函数f(x)的图象与直线y=x相切.
为偶函数,函数f(x)的图象与直线y=x相切.
(1)求f(x)的解析式
(2)若函数![]() 上是单调减函数,求k的取值范围.
上是单调减函数,求k的取值范围.
(1)∵f(x+1)为偶函数,
∴![]()
![]() 恒成立,
恒成立,
即(
∴
∴b=-
∴![]()
∵函数f(x)的图象与直线y=x相切,
∴二次方程![]() 有两相等实数根,
有两相等实数根,
∴![]()
![]()
(2)∵![]()
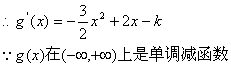
![]()
![]()
故k的取值范围为![]()
27.已知AB是抛物线![]() 的任一弦,F为抛物线的焦点,l为准线.m是过点A且以向量
的任一弦,F为抛物线的焦点,l为准线.m是过点A且以向量![]() 为方向向量的直线.
为方向向量的直线.
(1)若过点A的抛物线的切线与y轴相交于点C,求证:AF=CF;
(2)若![]() 异于原点),直线OB与m相交于点P,求点P的轨迹方程;
异于原点),直线OB与m相交于点P,求点P的轨迹方程;
(3)若AB过焦点F,分别过A,B的抛物线两切线相交于点T,求证:![]() 且T在直线l上.
且T在直线l上.
解:(1)设A(![]() ,因为导数
,因为导数![]() ,
,
则直线AC的方程:![]()
由抛物线定义知,AF=![]() +
+![]() ,又CF=
,又CF=![]() -(-
-(-![]() )=
)=![]() +
+![]() ,故AF=CF.
,故AF=CF.
(2)设![]()
由![]()
得![]() .
①
.
①
直线OB方程:![]() ②
②
直线m的方程:![]() , ③
, ③
由①②③得y=-p,故点P的轨迹方程为y=-p(x≠0).
(3)设![]() 则
则![]()
因为AB是焦点弦,设AB的方程为:![]()
得![]()
由(1)知直线AT方程:![]()
同理直线BT方程:![]()
所以直线AB方程:![]() ,
,
又因为AB过焦点,![]() ,故T在准线上.
,故T在准线上.
28.
|
(Ⅰ)求点P的轨迹方程;
(Ⅱ)若轨迹上的点P与同一平面上的点G、M分别满足
![]() ,
,
求以P、G、D为项点的三角形的面积.
解:(Ⅰ)![]()
∴点P的轨迹是D为焦点,l为相应准线的椭圆.
由![]()
以CD所在直线为x轴,以CD与⊙D的另一个交点O为坐标原点建立直角坐标系.
∴所求点P的轨迹方程为![]()
(Ⅱ)![]() G为椭圆的左焦点.
G为椭圆的左焦点.
又![]()
由题意,![]() (否则P、G、M、D四点共线与已经矛盾)
(否则P、G、M、D四点共线与已经矛盾)
![]()
又∵点P在椭圆上, ![]()
又![]()
![]()
29.设无穷数列{an}具有以下性质:①a1=1;②当![]()
(Ⅰ)请给出一个具有这种性质的无穷数列,使得不等式![]() 对于任意的
对于任意的![]() 都成立,并对你给出的结果进行验证(或证明);
都成立,并对你给出的结果进行验证(或证明);
(Ⅱ)若![]() ,其中
,其中![]() ,且记数列{bn}的前n项和Bn,证明:
,且记数列{bn}的前n项和Bn,证明:![]()
解:(Ⅰ)令![]() ,
,
则无穷数列{an}可由a1 =
1,![]() 给出.
给出.
显然,该数列满足![]() ,且
,且
![]()
(Ⅱ)![]()
![]()
又![]()
![]()
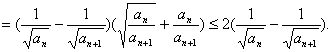
![]()
![]()
30、已知函数![]() 为偶函数,且其
为偶函数,且其
图像上相邻的一个最高点和最低点之间的距离为![]() 。
。
(1)求函数f(x)的解析式;
(2)若
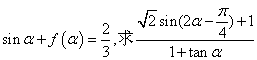 的值。
的值。
31.设![]() 分别为
分别为![]() 的重心和外心,
的重心和外心,![]() ,且
,且![]() 。
。
(I)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
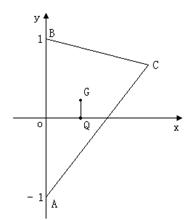 (II)若
(II)若![]() 是过点
是过点![]() 且垂直于
且垂直于![]() 轴的直线,是否存在直线
轴的直线,是否存在直线![]() ,使得
,使得![]() 与曲线
与曲线![]() 交于两个不同的点
交于两个不同的点![]() ,且
,且![]() 恰被
恰被![]() 平分?若存在,求出
平分?若存在,求出![]() 的斜率的取值范围;若不存在,请说明理由。
的斜率的取值范围;若不存在,请说明理由。
13.解:(I)设![]() ,则
,则![]() ,因为
,因为![]() ,可得
,可得![]() ;又由
;又由![]() ,
,
可得点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() 。
。
(II)假设存在直线![]() ,代入
,代入![]() 并整理得
并整理得
![]() ,
,
设![]() ,则
,则![]()
![]() 又
又![]()
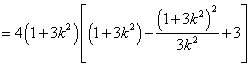
![]() ,解得
,解得![]() 或
或![]()
特别地,若![]() ,代入
,代入![]() 得,
得,![]() ,此方程无解,即
,此方程无解,即![]() 。
。
综上,![]() 的斜率的取值范围是
的斜率的取值范围是![]() 或
或![]() 。
。
18.已知△ABC中,三个内角是A、B、C的对边分别是a、b、c,其中c=10,且![]()
![]() (I)求证:△ABC是直角三角形;
(I)求证:△ABC是直角三角形;
(II)设圆O过A、B、C三点,点P位于劣弧AC上,∠PAB=60°,.求四边形ABCP的面积.
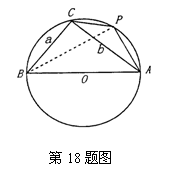 18.解:(Ⅰ)证明:根据正弦定理得,
18.解:(Ⅰ)证明:根据正弦定理得,![]()
整理为,sinAcosA=sinBcosB,即sin
∴![]() ∴
∴![]() .
.
![]()
![]() ∴舍去A=B. ∴
∴舍去A=B. ∴![]() 即
即![]() .
.
故△ABC是直角三角形.
(Ⅱ)解:由(1)可得:a=6,b=8.
在Rt△ACB中,![]()
∴![]()
=![]()
=![]()
连结PB,在Rt△APB中,AP=AB·cos∠PAB=5.
∴四边形ABCP的面积![]()
=24+![]()
![]() =18+
=18+![]() .
.
32.已知三次函数![]() 在
在![]() 和
和![]() 时取极值,且
时取极值,且![]() .
.
(1) 求函数![]() 的表达式;
的表达式;
(2) 求函数![]() 的单调区间和极值;
的单调区间和极值;
(3) 若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,试求
,试求![]() 、
、![]() 应满足的条件.
应满足的条件.
解:(1) ![]() ,
,
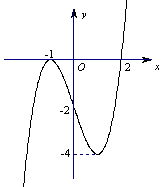 由题意得,
由题意得,![]() 是
是![]() 的两个根,
的两个根,
解得,![]() .
.
再由![]() 可得
可得![]() .
.
∴![]() .
.
(2) ![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
∴函数![]() 在区间
在区间![]() 上是增函数;
上是增函数;
在区间![]() 上是减函数;在区间
上是减函数;在区间![]() 上是增函数.
上是增函数.
函数![]() 的极大值是
的极大值是![]() ,极小值是
,极小值是![]() .
.
(3) 函数![]() 的图象是由
的图象是由![]() 的图象向右平移
的图象向右平移![]() 个单位,向上平移4
个单位,向上平移4![]() 个单位得到的,
个单位得到的,
所以,函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() (
(![]() ).
).
而![]() ,∴
,∴![]() ,即
,即![]() .
.
于是,函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() .
.
令![]() 得
得![]() 或
或![]() .
.
由![]() 的单调性知,
的单调性知,![]() ,即
,即![]() .
.
综上所述,![]() 、
、![]() 应满足的条件是:
应满足的条件是:![]() ,且
,且![]() .
.
易错问题
1.定义在![]() 上的偶函数
上的偶函数![]() 满足
满足![]() ,且在
,且在![]() 上是减函数,若
上是减函数,若![]() 是锐角三角形的两个内角,则
是锐角三角形的两个内角,则![]() 的大小关系为____ (答:
的大小关系为____ (答:![]() );
);
2.函数![]() 的图象与
的图象与![]() 轴的交点个数有____个(答:2)
轴的交点个数有____个(答:2)
3.如若函数![]() 是偶函数,则函数
是偶函数,则函数![]() 的对称轴方程是__ (答:
的对称轴方程是__ (答:![]() ).
).
4.(1)设![]() 成等差数列,
成等差数列,![]() 成等比数列,则
成等比数列,则![]() 的取值范围是____________.(答:
的取值范围是____________.(答:![]() )。
)。
(2)设![]() 成等差数列,
成等差数列,![]() 成等比数列,则
成等比数列,则![]() 的取值范围是____________.(答:
的取值范围是____________.(答:![]() )。
)。
5.已知函数![]() 过点
过点![]() 作曲线
作曲线![]() 的切线,求此切线的方程(答:
的切线,求此切线的方程(答:![]() 或
或![]() )。
)。
6.已知函数![]() 在区间[-1,2
]上是减函数,那么b+c有最__值__答:大,
在区间[-1,2
]上是减函数,那么b+c有最__值__答:大,![]() )
)
7.函数![]() 处有极小值10,则a+b的值为____(答:-7)
处有极小值10,则a+b的值为____(答:-7)
8.已知![]() ,
,![]() ,如果
,如果![]() 与
与![]() 的夹角为锐角,则
的夹角为锐角,则![]() 的取值范围是______(答:
的取值范围是______(答:![]() 或
或![]() 且
且![]() );
);
9.若点![]() 是
是![]() 的外心,且
的外心,且![]() ,则
,则![]() 的内角
的内角![]() 为____(答:
为____(答:![]() );
);
10.设集合![]() ,
,![]() ,
,![]() ,则
,则![]() _____(答:
_____(答:![]() )
)
11.![]() ,如果
,如果![]() ,求
,求![]() 的取值。(答:a≤0)
的取值。(答:a≤0)
已知函数![]() 在区间
在区间![]() 上至少存在一个实数
上至少存在一个实数![]() ,使
,使![]() ,求实数
,求实数![]() 的取值范围。 (答:
的取值范围。 (答:![]() )
)
12.已知O是△ABC所在平面内的一定点,动点P满足![]() ,
,![]() ,则动点P的轨迹一定通过△ABC的 (D)
,则动点P的轨迹一定通过△ABC的 (D)
A.内心 B.垂心 C.外心 D.重心
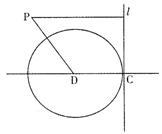
|
点F引圆![]() 的切线,切点为T,延长FT交
的切线,切点为T,延长FT交
双曲线右支于P点,若M为线段FP的中点,O为坐标
原点,则MO-MT与b-a的大小关系为 (B )
A.MO-MT > b-a
B.MO-MT = b-a
C.MO-MT < b-a
D.不确定
14.如图,![]() 所在的平面
所在的平面![]() 和四边形
和四边形![]() 所在的平面
所在的平面![]() 垂直,且
垂直,且![]() ,
, ![]() ,
, ![]() ,
,![]() ,
,![]() ,则点
,则点![]() 在平面
在平面![]() 内的轨迹是 (A )
内的轨迹是 (A )
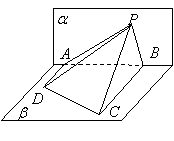 A.圆的一部分
A.圆的一部分
B.椭圆的一部分
C.双曲线的一部分
D.抛物线的一部分
15若函数![]() 的导函数为
的导函数为![]() ,则函数
,则函数![]() 的单调递减区间是(C )
的单调递减区间是(C )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
16.定义在R上的函数![]() ,它同时满足具有下述性质:
,它同时满足具有下述性质:
①对任何![]()
②对任何![]() 则
则![]() 0 .
0 .
17.设数列{an}是等比数列,![]() ,则a4与a10的等比中项为 ( )
,则a4与a10的等比中项为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
18.已知数列![]() 的前
的前![]() 项和
项和![]() 为非零常数),则数列
为非零常数),则数列![]() 为( )
为( )
(A)等差数列 (B)等比数列
(C)既不是等差数列,又不是等比数列 (D)既是等差数列又是等比数列
19.已知全集U=R,集合![]() ,则
,则
A.![]() B.
B.![]()
C.{(1,-2)} D.![]() ( )
( )
20. 已知椭圆![]() 的左右焦点分别为F1与F2,点P在直线l:
的左右焦点分别为F1与F2,点P在直线l:![]() 上,
上,
当![]() 取最大值时,点P的坐标为 (-10,-4)或(-2,4)
。
取最大值时,点P的坐标为 (-10,-4)或(-2,4)
。
21.椭圆![]() 的左右焦点分别为F1、F2,点P在椭圆上,若P,F1、F2是一个直角三角形的三个顶点,则P到X轴距离为 1或
的左右焦点分别为F1、F2,点P在椭圆上,若P,F1、F2是一个直角三角形的三个顶点,则P到X轴距离为 1或![]() .
.
22.过![]() 轴上一点
轴上一点![]() ,向圆
,向圆![]() 作切线,切点分别为
作切线,切点分别为![]() ,则
,则![]() 面积的最大值为
面积的最大值为 ![]() 。
。
已知向量![]() 是两个不共线的非零向量, 向量
是两个不共线的非零向量, 向量![]() 满足
满足![]() .则向量
.则向量![]() 用向量
用向量![]() 一定可以表示为
(C)
一定可以表示为
(C)
A.
![]() 且
且![]() . B.
. B. 
![]()
C.
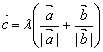
![]() D.
D. 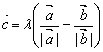
![]() , 或
, 或 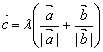
![]()
(5)若数列![]() 中,
中,![]() ,且对任意的正整数
,且对任意的正整数![]() 、
、![]() 都有
都有![]() ,则
,则![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]() ( C)
( C)
16.已知x∈N*,f(x)= 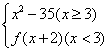 ,其值域设为D,给出下列数值:-26,-1,9,14,27,65,则其中属于集合D的元素 ___14,65 _
_.(写出所有可能的数值)
,其值域设为D,给出下列数值:-26,-1,9,14,27,65,则其中属于集合D的元素 ___14,65 _
_.(写出所有可能的数值)
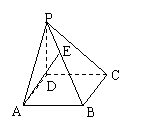 23、如图,
23、如图,![]() 垂直正方形
垂直正方形![]() 所在的平面,
所在的平面,![]() ,动点
,动点![]() 在线段
在线段![]() 上,则二面角
上,则二面角![]() 的取值范围是
的取值范围是
A、![]() B、
B、![]()
C、![]() D、
D、![]()
24.在△OAB(O为原点)中,![]() ,若
,若![]() ,则S△AOB的值为 ( )
,则S△AOB的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
25.若y=3x(x∈[a,b])的值域为[1,9],则a2+b2-
A.[2,4] B.[4,16] C.[2,2] D.[4,12]
26.在等比数列![]() 中,
中,![]() ,前
,前![]() 项和为
项和为![]() ,若数列
,若数列![]() 也是等比数列,
也是等比数列,
则![]() 等于( C )
等于( C )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
27、点P在平面上作匀速直线运动,速度向量![]() =(4,-3)(即点P的运动方向与
=(4,-3)(即点P的运动方向与![]() 相同,且每秒移动的距离为
相同,且每秒移动的距离为![]() 个单位.设开始时点P的坐标为(-10,10),则5秒后点P的坐标为( D )
个单位.设开始时点P的坐标为(-10,10),则5秒后点P的坐标为( D )
(A)(-2,4) (B)(-30,25) (C)(5,-10) (D)(10,-5)
28、已知在△ABC中,∠ACB=90°,BC=3,AC=4,P是AB上的点,则点P到AC、BC
的距离乘积的最大值是 3 。
29、若函数![]() 内为增函数,则实数a的取值范围(A )
内为增函数,则实数a的取值范围(A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
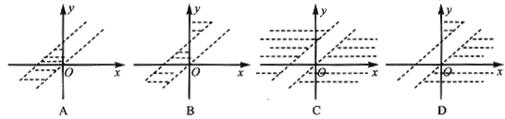
 30、如图,平面内的两条相交直线
30、如图,平面内的两条相交直线![]() 和
和![]() 将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ (不包括边界). 若
将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ (不包括边界). 若![]() ,且点
,且点![]() 落在第Ⅲ部分,则实数
落在第Ⅲ部分,则实数![]() 满足( B
)
满足( B
)
(A) ![]() .
(B)
.
(B) ![]() .
.
(C) ![]() .
(D)
.
(D) ![]() .
.
31.已知双曲线![]() 的焦点分别为F1、F2,点P在双曲线上且PF1
=4PF2,则双曲线离心率的最大值为(
B )
的焦点分别为F1、F2,点P在双曲线上且PF1
=4PF2,则双曲线离心率的最大值为(
B )
A.![]() B.
B.![]() C.2 D.
C.2 D.![]()
8、某班有48名学生,某次数学考试,算术平均分为70分,标准差为s,后来发现成绩记录有误,某甲得80分却误记为50分,某乙得70分却误记为100分,更正后计算得标准差为s1,则s1和s之间的大小关系为 …………………………………………………(D )
(A) s1>s (B) s1=s (C) s+5<s1 (D) s>s1
15.在ABC中,若:= = ,则COSA等于_![]() __________.
__________.
4、已知等差数列{an}的首项a1=120,d=-4,记Sn= a1+a2+…+an,若Sn≤an(n>1),则n最小值为………………………………………………………………………………(B )
(A)60 (B)62 (C)63 (D)70
7.二元函数![]() 定义域为
定义域为![]() ,则函数
,则函数![]() 的定义域所表示的平面区域是(B)
的定义域所表示的平面区域是(B)
|
9、一条走廊宽 ![]()
![]() 的整块地砖来铺设(每块地砖都是单色的, 每种颜色的地砖都足够多), 要求相邻的两块地砖颜色不同, 那么所有的不同拼色方法有
( D)
的整块地砖来铺设(每块地砖都是单色的, 每种颜色的地砖都足够多), 要求相邻的两块地砖颜色不同, 那么所有的不同拼色方法有
( D)
(A)![]() 个 (B)
个 (B) ![]() 个 C.
个 C. ![]() 个 (D)
个 (D) ![]() 个
个
(18)已知等比数列{an}的前n项和为Sn.
(Ⅰ)若Sm,Sm+2,Sm+1成等差数列,证明am,am+2,am+1成等差数列;
(Ⅱ)写出(Ⅰ)的逆命题,判断它的真伪,并给出证明.
证 (Ⅰ) ∵Sm+1=Sm+am+1,Sm+2=Sm+am+1+am+2.
由已知2Sm+2=Sm+Sm+1,∴ 2(Sm+am+1+am+2)=Sm+(Sm+am+1),
∴am+2=-am+1,即数列{an}的公比q=-.
∴am+1=-am,am+2=am,∴2am+2=am+am+1,∴am,am+2,am+1成等差数列.
(Ⅱ) (Ⅰ)的逆命题是:若am,am+2,am+1成等差数列,则Sm,Sm+2,Sm+1成等差数列.
设数列{an}的公比为q,∵am+1=amq,am+2=amq2.
由题设,2am+2=am+am+1,即2amq2=am+amq,即2q2-q-1=0,∴q=1或q=-.
当q=1时,A≠0,∴Sm, Sm+2, Sm+1不成等差数列.
逆命题为假.
19. (12分)设某物体一天中的温度T是时间t的函数,![]() ,
,![]() 其中温度的单位是
其中温度的单位是![]() ,时间的单位是小时。t=0表示12:00, t取正值表示12:00点以后。若测得该物体在8:00的温度为8
,时间的单位是小时。t=0表示12:00, t取正值表示12:00点以后。若测得该物体在8:00的温度为8![]() ,12:00的温度为60
,12:00的温度为60![]() ,13:00的温度为58
,13:00的温度为58![]() ,且已知该物体的温度在8:00和16:00有相同的变化率。
,且已知该物体的温度在8:00和16:00有相同的变化率。
(1)写出该物体的温度T关于时间t的函数关系式;
(2)该物体在10:00到14:00这段时间中(包括10:00,14:00)何时温度最高?并求出最高温度。
(1)![]() 依题意得
依题意得
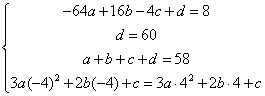
解得:a=1,b=0,c=-3,d=60 故T(t)=t3-3t+60
(2)![]() =0,得:
=0,得:![]()
比较T(-2),T(-1),T(1),T(2)知,在10:00![]() 14:00这段时间中,该物体在11:00和14:00的温度最高,且最高温度为62
14:00这段时间中,该物体在11:00和14:00的温度最高,且最高温度为62![]() .
.