08届高考数学复习试题精选(二)
卞志业 2008-1-17
1.(0710吉林一中)已知![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2. (0711东北师大)采取简单随机抽样,从含有6个个体的总体中抽取一个容量为3的样本,个体a前两次未被抽到,第三次被抽到的概率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. (0711东北师大)设函数f(x),对任意的实数x、y,有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,则f(x)在区间![]() 上 ( )
上 ( )
A.有最大值f(a) B.有最小值f(a)
C.有最大值![]() D. 有最小值
D. 有最小值![]()
4.(0712福建莆田)给出下列四个命题:①若直线a∥平面α,直线b⊥α,则a⊥b;②若直线a∥平面α,α⊥平面β,则a⊥β;③若a、b是二条平行直线,b![]() 平面α,则a∥α;④若平面α⊥平面β,平面γ⊥β,则α∥γ。其中正确的命题是 (
)
平面α,则a∥α;④若平面α⊥平面β,平面γ⊥β,则α∥γ。其中正确的命题是 (
)
(A)。① ( B)、② (C)、③ ( D)、④
5. (0712福建莆田)已知单位向量![]() ,
,![]() 的夹角为
的夹角为![]() ,那么
,那么![]() +2
+2![]() 等于 ( )
等于 ( )
A.![]() B.3 C.
B.3 C.![]() D.
D.![]()
6.(0711广州汕头)函数![]() 图象的一个对称中心是( )
图象的一个对称中心是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.(0711安徽舒城)已知等差数列{an}的前n项和为Sn,且S2=10,S5=55,则过点P(n,![]() ),Q(n+3,
),Q(n+3,![]() ) (n∈N*)的一次函数解析式是
) (n∈N*)的一次函数解析式是
A.y=2x+1 B.y=![]() C.y=
C.y=![]() x-1 D.y=2x-1
x-1 D.y=2x-1
8.(0711广东六校联考)数列![]() 中,
中,![]()
![]() ,则
,则![]() =
=
A. ![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
 9.(0711广东六校联考)
已知函数
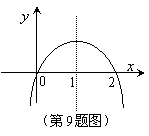
9.(0711广东六校联考)
已知函数![]() ,其导数
,其导数![]() 的图象如右图,则函数
的图象如右图,则函数![]() 的极小值是(
)
的极小值是(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.(0710吉林一中)甲、乙两人相约10天之内在某地会面,约定先到的人等候另一个人,经过3天以后方可离开,若他们在限期内到达目的的地的时间是随机的,则甲、乙两人能会面的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
11.(0711广东六校联考)数列![]() 中,
中,![]()
![]() ,则
,则![]() =( )
=( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
12.(0710吉林一中)设![]() 是定义在R上以2为周期的偶函数,已知
是定义在R上以2为周期的偶函数,已知![]() ,则
,则![]() 在(1,2)上 ( )
在(1,2)上 ( )
A.是增函数,且![]() B.是增函数,且
B.是增函数,且![]()
C.是减函数,且![]() D.是减函数,且
D.是减函数,且![]()
13.(0710吉林一中)(理)![]() .
.
13. (0711安徽舒城)已知![]() 在x处的切线斜率为
在x处的切线斜率为![]() ,且数列
,且数列![]() 为递增数列,则a的取值范围是
。
为递增数列,则a的取值范围是
。
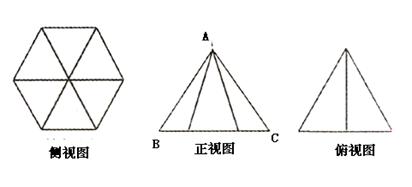
14.(0710吉林一中)一个几何的三视图如图所示:其中,正视图中△ABC的边长是2的正三角形,俯视图为正六边形,那么该几何体几的体积为
. 
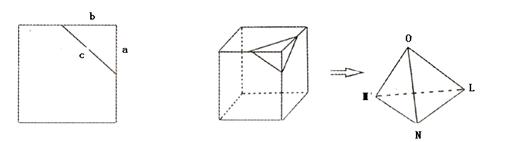
15.(0710吉林一中)在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有:![]()
设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O—LMN,如果用![]() 表示三个侧面面积,
表示三个侧面面积,![]() 表示截面面积,那么你类比得到的结论是
.
表示截面面积,那么你类比得到的结论是
.
16.(0710吉林一中)给出下列四个命题:
①存在![]() 是奇函数;
是奇函数;
②要得到函数![]() 的图象,只要将函数
的图象,只要将函数![]() 个单位;
个单位;
③函数![]()
④函数![]() 的图象既是中心对称图形,又是轴对称图形.
的图象既是中心对称图形,又是轴对称图形.
其中,真命题的编号是 .(写出所有真命题的编号)
17.
(0710吉林一中)已知函数![]()
![]() ,
,
![]() 相邻两对称轴间的距离不小于
相邻两对称轴间的距离不小于![]()
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)在![]()
![]()
![]() 的面积.
的面积.
18.
(0710吉林一中)已知二次函数![]() 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为![]() 的图象上.
(Ⅰ)求数列
的图象上.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() 都成立的最小正整数m.
都成立的最小正整数m.
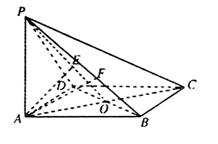
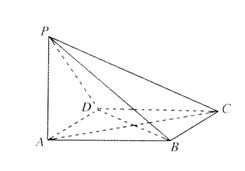
19.(0710吉林一中)如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
(Ⅰ)求证:平面PBD⊥平面PAC;
(Ⅱ)求点A到平面PBD的距离;
(Ⅲ)求二面角A—PB—D的余弦值.
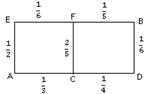 20.理(0711东北师大)某人居住在A处,准备开车到B处上班.若各路段发生堵车都是相互独立的,同一路段发生堵车最多只有一次,发生堵车的概率如图(例如:
20.理(0711东北师大)某人居住在A处,准备开车到B处上班.若各路段发生堵车都是相互独立的,同一路段发生堵车最多只有一次,发生堵车的概率如图(例如: ![]() 算作两段:路段AC发生堵车的概率为
算作两段:路段AC发生堵车的概率为![]() , 路段CD发生堵车的概率为
, 路段CD发生堵车的概率为![]() ).
).
(1)请你为其选择一条由A到B的路线,使不堵车的概率最大;
(2)求路线![]() 中遇到堵车次数的期望.
中遇到堵车次数的期望.
20. (07山东高考)设![]() 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量![]() 表示方程
表示方程![]() 实根的个数(重根按一个计).
实根的个数(重根按一个计).
(I)求方程![]() 有实根的概率;
有实根的概率;
(II)求在先后两次出现的点数中有5的条件下,方程![]() 有实根的概率.
有实根的概率.
21. (0710吉林一中)
已知函数![]()
![]() ,且在点P处的切线与直线
,且在点P处的切线与直线![]()
(Ⅰ)若![]() ,试求函数
,试求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() 的单调递增区间,试求
的单调递增区间,试求![]() 的范围.
的范围.
22.(0710吉林一中)已知定点F(1,0),动点P在y轴上运动,过点P做PM交x轴于点M,并延长MP到点N,且![]()
(Ⅰ)求点N的轨迹方程;
(Ⅱ)直线l与点N的轨迹交于A、B不同两点,若![]() ,且
,且![]() ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
08届高考数学复习试题精选(二)答案
一、选择题:本大题主要考查基本知识和基本运算 共12小题,每小题5分,满分60分.
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 | C | C | A | A | C | B | A | B | D | D | B | D |
二、填空题: 本大题主要考查基本知识和基本运算. 本大题共4小题,每小题4分,满分16分。
13. ![]()
![]() 14.
14. ![]() _
_
15. ![]() 16. ①③
16. ①③
三、解答题: 本大题共6小题,其中17~21题每题12分,22题14分,满分74分.解答应写出文字说明、演算步骤或推证过程.
17.解: (Ⅰ)![]()
![]()
![]() ………………3分
………………3分
![]()
![]() ……………4分
……………4分
由题意可知![]()
解得![]() ……………………5分
……………………5分
(Ⅱ)由(Ⅰ)可知![]() 的最大值为1,
的最大值为1,
![]()
![]()
![]() ……………6分
……………6分
而![]()
![]()
![]() ………………8分
………………8分
由余弦定理知![]()
![]() …10
…10
联立解得![]() ………11分
………11分![]() ……12分
……12分
(或用配方法![]()
![]() )
)
18.解: (Ⅰ)设二次函数为![]() …………1分
…………1分
![]()
![]()
![]()
![]() ……3分,又
……3分,又![]() 的图象上.
的图象上.
![]() ………………………………4分
………………………………4分
当![]() ……5分
……5分
当![]() ,满足上式
,满足上式
![]() ………………………………6分
………………………………6分
(Ⅱ)由(Ⅰ)得:![]() ………8分
………8分
故![]()
![]() ……………………10分
……………………10分
要使![]() 都成立 必须且只须
都成立 必须且只须![]()
![]()
![]() …………12分
…………12分
|
(Ⅰ)证明:设AC与BD交于O,连结PO

![]() ……………………(3分)
……………………(3分)
又![]()
![]() ……………………(4分)
……………………(4分)
(Ⅱ)作![]()
![]()
所以AE为点A到平面PBD的距离.…………(6分)
在![]()
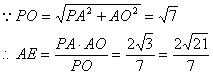 ,所以A点到平面PBD的距离为
,所以A点到平面PBD的距离为![]() …8分
…8分
(Ⅲ)作![]()
![]()
![]()
![]() …10分
…10分
在![]() ,
,
![]()
|
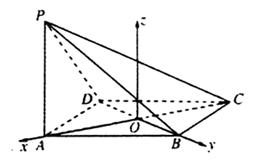
解法二:(Ⅰ)设AC与BD交于O点
![]()
以OA、OB所在直线分别x轴,y轴.
以过O且垂直平面ABCD的直线为z轴,建立
如图的空间直角坐标系,则
![]()
![]() …………………………2分
…………………………2分
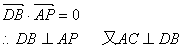
![]()
![]() ……(4分)
……(4分)
(Ⅱ)设平面PDB的法向量为![]() ,
,![]()
由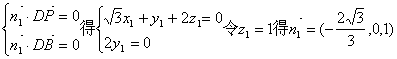 …………6分
…………6分
 =
=![]() …………8分
…………8分
(Ⅲ)设平面ABP的法向量![]()
![]()
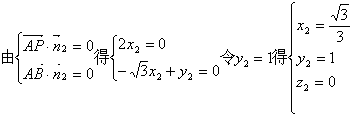
![]() …10分
…10分
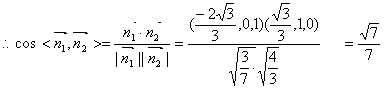 …………11分
…………11分
所以二面角A—PB—D的余弦值为![]() …………12分
…………12分
20.解:记AEFB表示![]() 不堵车,其它类似.
不堵车,其它类似.
(1) P(AEFB)=![]() , P(ACDB)=
, P(ACDB)=![]() ,P(ACFB)=
,P(ACFB)=![]() ,
,
![]()
![]() ,
,
![]()
![]() 为最佳路线.
为最佳路线.
(2)设![]() 表示
表示![]() 中堵车次数.则
中堵车次数.则![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
20.
解::(I)基本事件总数为![]() ,
,
若使方程有实根,则![]() ,即
,即![]() 。
。
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
目标事件个数为![]()
因此方程![]() 有实根的概率为
有实根的概率为![]()
(II) 记“先后两次出现的点数中有5”为事件M,“方程![]() 有实根” 为事件N,则
有实根” 为事件N,则![]() ,
,![]() ,
,
![]() .
.
21.解:(1)由![]() ①……1分
①……1分
又![]()
![]() ,
, ![]() ②…3分
②…3分
又![]() ①、②联立得:
①、②联立得:![]()
![]() ……4分
……4分
![]()
![]() 的单调递减区间.…6分
的单调递减区间.…6分
(2)令![]()
又![]()
![]()
即![]() 单调递增区间.
单调递增区间.
![]() …………………………8分
…………………………8分
由(1)知:![]()
![]()
![]() ………10分
………10分
![]() ……11分
……11分
由![]()
![]()
![]() ……………12分
……………12分
另解:由![]() 得:
得:![]()
![]()
![]()
![]() …10分
…10分 ![]() ……12分
……12分
注:若用b表示a,酌情给分.
22.解: (Ⅰ)由于![]() 则P为MN的中心,……1分,
则P为MN的中心,……1分,
设N(x,y),则M(-x,0),P(0,![]() ),……(2分),由
),……(2分),由![]() 得
得![]()
![]()
![]() 所以点N的轨迹方程为
所以点N的轨迹方程为![]() ……5分
……5分
(Ⅱ)设直线l的方程是![]() 与
与![]() :
:
![]() ……………………6分
……………………6分
设![]() 则:
则:![]()
![]()
![]() ……………………7分
……………………7分
由![]()
![]() 即
即![]()
![]() …………9分
…………9分
由于直线与N的轨迹交于不同的两点,则![]()
把![]()
![]() ………………10分
………………10分
而![]()
![]()
![]()
![]()
![]() …11分
…11分
又因为![]()
![]()
解得![]()
综上可知k的取值范围是![]() .…14分
.…14分