08届高考文科数学2月测试卷
数学(文科)
一．选择题：本大题共10个小题；每小题5分，共50分．在每小题给出的四个选项中，有且只有一项是符合题目要求的．
1．若集合满足{3}
B{1,2,3},则集合B的个数是（ ）。
A．1 B．3 C．4 D．8
2．已知
是虚数单位，则复数
等于（ ）。
A．
B．
C．
D．
3．函数
的最小正周期为（ ）
A．1 B．2 C．3 D．4
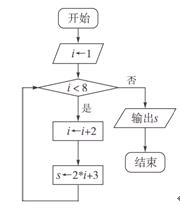
4．如图2给出的算法流程图中，输出的结果s=（ ）. 图2
A．19 B．25 C．23 D．21
5．数列三个实数a、b、c成等比数列，若a+b+c=1成立，则b取值范围是 （ ）
A．[0，
] B．[－1，] C．[－，0] D．
（0，]
6．为确保信息安全，信息需加密传输，发送方由明文→密文(加密)，接收方由密文→明文(解密)，已知加密规则为：明文
，
，
对应密文
，
，
.例如,明文1，2，3对应密文7，14，6. 当接收方收到密文16，30，14时，则解密得到的明文为（ ）
A．2，4，7 B．2，7，4 C．4，2，7 D．7，4，2
7.对于平面
和共面的直线
、
下列命题中真命题是
A．若
则
B．若
则
C．若
则 D．若、
与所成的角相等，则
8．
为圆
内异于圆心的一点，则直线
与该圆的位置关系为（ ）
A．相离 B．相交 C．相切 D．相切或相离
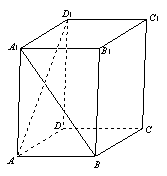9．如图，正棱柱
中，
，则异面直线
与
所成角的余弦值为
A．
B．
C．
D．
10．定义新运算
：当
时，
；当
时, 
，则函数
， 
的最大值等于( )
A．-1 B．1 C． 2 D． 12
第Ⅱ卷 (非选择题共100分)
二． 填空题：本大题共4个小题，每小题5分，满分20分．
11．已知
，若
的夹角为钝角， 则实数
的取值范围为
．
12．有三颗骰子A、B、C，A的表面分别刻有1，2，3，4，5，6，B的表面分别刻有1，3，5，7，9，11，C的表面分别刻有2，4，6，8，10，12，则抛掷三颗骰子后向上的点数之和为12的概率是
13．在等差数列
中，若
的值为_______
14．设实数x, y满足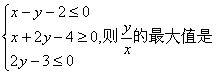
三．解答题：本大题6小题，共80分．解答应写出文字说明，证明过程或演算步骤．
15．(本小题满分14分)
已知函数
的最大值为1.
（1）求常数的值；
（2）求
的单调递增区间；
（3）求
成立的
的取值集合。
16．(本小题满分12分)
设
为公差大于0的等差数列，
为数列的前n项的和．已知
，
．
（1）求数列的通项公式
；
（2）若
，证明：数列
的前n项和
<
．
17. （本小题满分14分）
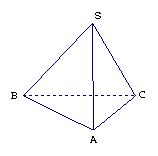在三棱锥
中，
,
.
(1) 求三棱锥的体积；
(2) 证明:
;
(3) 求二面角C-SA-B的大小。
18．（本小题14分）
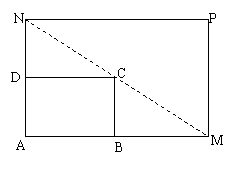
如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN，要求B在AM上，D在AN上，且对角线MN过C点，已知AB＝3米，AD＝2米，
（1） 要使矩形AMPN的面积大于32平方米，则AN的长应在什么范围内？
（2）
若AN 
（单位：米），则当AM、AN的长度是多少时，矩形花坛AMPN的面积最大？并求出最大面积．
19．（本小题满分12分）
（1）求经过点A（5，2），B（3，2），圆心在直线2x-y-3=0上圆方程；
（2）设圆上的点A（2，3）关于直线x+2y=0的对称点仍在这个圆上，且与直线x-y+1=0相交的弦长为
，求圆方程。
20．（本小题满分14分）
已知二次函数
满足条件：① 
； ② 的最小值为
.
(1) 求函数的解析式；
(2) 设数列
的前项积为
, 且
, 求数列的通项公式；