高考数学三角函数复习测试题
选择题
1.对任意的锐角α,β,下列不等关系中正确的是 ( )
(A)sin(α+β)>sinα+sinβ (B)sin(α+β)>cosα+cosβ
(C)cos(α+β)<sinα+sinβ (D)cos(α+β)<cosα+cosβ
2.当![]() 时,函数
时,函数![]() 的最小值为 ( )
的最小值为 ( )
(A)2 (B)![]() (C)4 (D)
(C)4 (D)![]()
3.在![]() 中,已知
中,已知![]() ,给出以下四个论断: ( )
,给出以下四个论断: ( )
① ![]() ②
② ![]()
③ ![]() ④
④ ![]()
其中正确的是(A)①③ (B)②④ (C)①④ (D)②③
4函数f (x) = sin x +cos x 的最小正周期是 ( )
(A) ![]() (B)
(B)![]()
![]() (C)
(C)![]() (D)2
(D)2![]()
5.已知函数y
=tan ![]() 在(-
在(-![]() ,
,![]() )内是减函数,则 ( )
)内是减函数,则 ( )
(A)0 < ![]() ≤ 1 (B)-1 ≤
≤ 1 (B)-1 ≤ ![]() < 0 (C)
< 0 (C)![]() ≥ 1 (D)
≥ 1 (D)![]() ≤ -1
≤ -1
6.锐角三角形的内角A 、B 满足tan A - ![]() = tan B,则有 ( )
= tan B,则有 ( )
(A)sin 2A –cos B = 0 (B)sin 2A + cos B = 0
(C)sin 2A – sin B = 0 (D) sin 2A+ sin B = 0
7.设![]() ,且
,且![]() ,则 ( )
,则 ( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
8.![]() ( )
( )
(A) ![]() (B)
(B) ![]() (C)
1
(D)
(C)
1
(D)![]()
9.已知k<-4,则函数y=cos2x+k(cosx-1)的最小值是( )
(A) 1 (B) -1 (C) 2k+1 (D) -2k+1
10.已知![]() ( )
( )
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
11.设函数![]() 为 ( )
为 ( )
A.周期函数,最小正周期为![]() B.周期函数,最小正周期为
B.周期函数,最小正周期为![]()
C.周期函数,数小正周期为![]() D.非周期函数
D.非周期函数
12.在△OAB中,O为坐标原点,![]() ,则当△OAB的面积达最大值时,
,则当△OAB的面积达最大值时,![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13、若![]() ,则
,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
14.若![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
15.![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
C.![]() D.
D.![]()
17函数![]() 在下列哪个区间上是减函数 ( )
在下列哪个区间上是减函数 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
18函数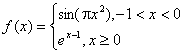 ,若
,若![]() ,则
,则![]() 的所有可能值为 (A)1
(B)
的所有可能值为 (A)1
(B)![]() (C)
(C)![]() (D)
(D)![]() ( )
( )
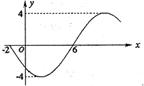 19函数
19函数![]() 的部分图象如图所示,则函数表达式为( )
的部分图象如图所示,则函数表达式为( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
填空题:
20已知tan ![]() =2,则tanα的值为-
=2,则tanα的值为-![]() ,tan
,tan![]() 的值为
的值为
21设a为第四象限的角,若 ![]() ,则tan 2a =______________.
,则tan 2a =______________.
22.函数![]() 的图象与直线
的图象与直线![]() 有且仅有两个不同的交点,则
有且仅有两个不同的交点,则![]() 的取值范围是__________。
的取值范围是__________。
23.函数![]() 的最小正周期T=__________。
的最小正周期T=__________。
24若![]() ,
,![]() ,则
,则![]() =__________。
=__________。
25.函数![]() 的最小正周期与最大值的和为
.
的最小正周期与最大值的和为
.
26.设函数f (x)的图象与直线x =a,x =b及x轴所围成图形的面积称为函数f(x)在[a,b]上的面积,已知函数y=sinnx在[0,![]() ]上的面积为
]上的面积为![]() (n∈N* )(i)y=sin3x在[0,
(n∈N* )(i)y=sin3x在[0,![]() ]上的面积为
]上的面积为 ![]() ;(ii)y=sin(3x-π)+1在[
;(ii)y=sin(3x-π)+1在[![]() ,
,![]() ]上的面积为 .
]上的面积为 .
27.已知![]() 、
、![]() 均为锐角,且
均为锐角,且![]() =
.
=
.
解答题:
28.
化简![]() 并求函数
并求函数![]() 的值域和最小正周期.
的值域和最小正周期.
29 已知![]() =2,求
=2,求
(I)![]() 的值; (II)
的值; (II)![]() 的值.
的值.
.
30设函数![]() 图像的一条对称轴是直线
图像的一条对称轴是直线![]() 。(Ⅰ)求
。(Ⅰ)求![]() ;(Ⅱ)求函数
;(Ⅱ)求函数![]() 的单调增区间;(Ⅲ)画出函数
的单调增区间;(Ⅲ)画出函数![]() 在区间
在区间![]() 上的图像。
上的图像。
31已知![]() 为第二象限的角,
为第二象限的角,![]() ,
,![]() 为第一象限的角,
为第一象限的角,![]() .求
.求![]() 的值.
的值.
32.已知函数f(x)=-![]() sin2x+sinxcosx.
sin2x+sinxcosx.
(Ⅰ) 求f(![]() )的值; (Ⅱ) 设
)的值; (Ⅱ) 设![]() ∈(0,
∈(0,![]() ),f(
),f(![]() )=
)=![]() -
-![]() ,求sin
,求sin![]() 的值.
的值.
33.已知函数f(x)=2sinxcosx+cos2x.
(Ⅰ) 求f(![]() )的值;(Ⅱ) 设
)的值;(Ⅱ) 设![]() ∈(0,
∈(0,![]() ),f(
),f(![]() )=
)=![]() ,求sin
,求sin![]() 的值.
的值.
34.
已知向量![]() .
.
求函数f(x)的最大值,最小正周期,并写出f(x)在[0,π]上的单调区间.
35. 已知在△ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos2C=0,求角A、B、C的大小.
36.若函数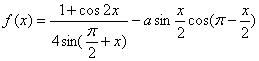 的最大值为2,试确定常数a的值.
的最大值为2,试确定常数a的值.
37.
已知![]() . (I)求sinx-cosx的值;
. (I)求sinx-cosx的值;
(Ⅱ)求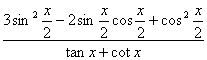 的值.
的值.
38已知向量
![]() ,
,
求![]() 的值.
的值.
39已知![]() .
.
,