高考数学不等式复习测试题
1．对于
，给出下列四个不等式
①
②
③
④
其中成立的是 ( D )
A．①与③ B．①与④ C．②与③ D．②与④
2.设z=x—y ,式中变量x和y满足条件
则z的最小值为
（ A ）
(A) 1 (B) –1 (C) 3 (D) –3
3．不等式
的解集是 （
A ）
A．
B．
C．
D．
4．不等式
的解集为 （ A ）
A． 
B．
C． 
D．
5．一元二次方程
有一个正根和一个负根的充分不必要条件是： （ C ）
A．
B．
C．
D．
6． 若
是等差数列，首项
，则使前n项和
成立的最大自然数n是： （
B ）
A．4005 B．4006 C．4007 D．4008
7．已知a、b、c满足
，且
，那么下列选项中不一定成立的是 （ C ）
A．
B．
C． 
D．
8．函数
上的最大值和最小值之和为a，则a的值为
（ B ）
A．
B．
C．2 D．4
9．若
，则下列不等式①
；②
③
；
④
中，正确的不等式有 （ B ）
A．1个 B．2个 C．3个 D．4个
10．设集合
，那么点P（2，3）
的充要条件是（ A ）
A．
B．
C．
D．
11．设
则以下不等式中不恒成立的是 （
B ）
A．
B．
C．
D．
12．命题p：若a、b∈R，则a+b>1是a+b>1的充分而不必要条件；
命题q：函数y=
的定义域是（－∞，－1
∪[3，+∞
.则 （
D ）
A．“p或q”为假 B．“p且q”为真
C．p真q假 D．p假q真
13．
的最小值为
（ B ）
A．
－ B．－ C．－－ D．+
14．不等式
的解集为 （ A ）
A．
B．
C．
D．
15．设函数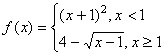
，则使得
的自变量
的取值范围为
（ A ）
A．
B．
C．
D．
16．不等式
的解集为 （
D ）
A．
B．
C．
D．
17．不等式x+2≥x的解集是 {xx≥－1} .
18.已知
则不等式
≤5的解集是 
.
19．在函数
中，若a，b，c成等比数列且
，则
有最____大__________值（填“大”或“小”），且该值为_____-3_________.
20．某村计划建造一个室内面积为800
的矩形蔬菜温室。在温室内，沿左．右两侧与后侧内墙各保留1
宽的通道，沿前侧内墙保留3宽的空地。当矩形温室的边长各为多少时？蔬菜的种植面积最大。最大种植面积是多少？
本小题主要考查把实际问题抽象为数学问题，应用不等式等基础知识和方法解决问题的能力.
解：设矩形温室的左侧边长为a m，后侧边长为b m，则 ab=800.
蔬菜的种植面积 
所以 
当
答：当矩形温室的左侧边长为40m，后侧边长为20m时，蔬菜的种植面积最大，最大种植面积为648m2.
21．已知数列
的前
项和
满足
.
（1）写出数列的前三项
；
（2）求数列的通项公式；
（3）证明：对任意的整数
，有
.
本小题主要考查数列的通项公式，等比数列的前n项和以及不等式的证明.考查灵活运用数学知识分析问题和解决问题的能力.
（Ⅰ）解：由
由
由
（Ⅱ）解：当
时，有
……
所以
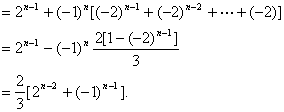
经验证a1也满足上式，所以 
（Ⅲ）证明：由通项公式得
当
且n为奇数时， 
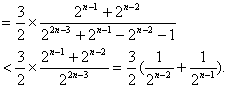
当
为偶数时，
当为奇数时，
所以对任意整数m>4，有
22．已知函数
满足下列条件：对任意的实数x1，x2都有
和
，其中
是大于0的常数.
设实数a0，a，b满足
和
(Ⅰ)证明
，并且不存在
，使得
；
(Ⅱ)证明
；
(Ⅲ)证明
.
本小题主要考查函数、不等式等基本知识，以及综合运用数学知识解决问题的能力.满分14分.
证明：（I）任取
和
②
可知 
，
从而 
. 假设有
①式知
∴不存在
（II）由
③
可知
④
由
①式，得
⑤
由
和②式知，
⑥
由⑤、⑥代入④式，得 
（III）由③式可知
（用②式）
（用①式）
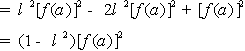
23．如图，直线
相交于点P.直线l1与x轴交于点P1，过点P1作x轴的垂线交直线l2于点Q1，过点Q1作y轴的垂线交直线l1于点P2，过点P2作x轴的垂线交直线l2于点Q2，…，这样一直作下去，可得到一系列点P1、Q1、P2、Q2，…，点Pn（n=1，2，…）的横坐标构成数列
|
；
（Ⅱ）求数列
的通项公式；
（Ⅲ）比较
的大小.
（Ⅰ）证明：设点Pn的坐标是
，由已知条件得
点Qn、Pn+1的坐标分别是：
由Pn+1在直线l1上，得 
所以 
即 
（Ⅱ）解：由题设知 
又由（Ⅰ）知 
，
所以数列 
是首项为
公比为
的等比数列.
从而
（Ⅲ）解：由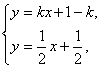
得点P的坐标为（1，1）.
所以
（i）当
时，
>1+9=10.
而此时 
（ii）当
时，<1+9=10.
而此时 
24．某企业2003年的纯利润为500万元，因设备老化等原因，企业的生产能力将逐年下降.若不能进行技术改造，预测从今年起每年比上一年纯利润减少20万元，今年初该企业一次性投入资金600万元进行技术改造，预测在未扣除技术改造资金的情况下，第n年（今年为第一年）的利润为500(1+
)万元（n为正整数）.
（Ⅰ）设从今年起的前n年，若该企业不进行技术改造的累计纯利润为An万元，进行技术改造后的累计纯利润为Bn万元（须扣除技术改造资金），求An、Bn的表达式；
（Ⅱ）依上述预测，从今年起该企业至少经过多少年，进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润？
本小题主要考查建立函数关系式、数列求和、不等式的等基础知识，考查运用数学知识解决实际问题的能力.满分12分.
解：（Ⅰ）依题设，An=(500－20)+(500－40)+…+(500－20n)=490n－10n2；
Bn=500[(1+)+(1+
)+…+(1+)]－600=500n－
－100.
（Ⅱ）Bn－An=(500n－－100) －(490n－10n2)
=10n2+10n－－100=10[n(n+1) － 
－10].
因为函数y=x(x+1) －
－10在（0，+∞）上为增函数，
当1≤n≤3时，n(n+1) － －10≤12－
－10<0；
当n≥4时，n(n+1) － －10≥20－
－10>0.
∴仅当n≥4时，Bn>An.
答：至少经过4年，该企业进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润.