高考数学数列专题测试卷
一、选择题
1．已知等差数列
中，
，则
的值是（
）
A．15 B．30 C．31 D．64
2．在各项都为正数的等比数列
中，首项
，前三项和为21，则
=（ ）
A．33 B．72 C．84 D．189
3．如果
，
，…，
为各项都大于零的等差数列，公差
，则（ ）
（A）
（B）
（C）+
+
（D）=
4．将1，2，…，9这9个数平均分成三组，则每组的三个数都成等差数列的概率为（ ）
A．
B．
C．
D．
5．已知数列
（ ）
A．
B．3 C．4 D．5
6．一给定函数
的图象在下列图中，并且对任意
，由关系式
得到的数列
满足
，则该函数的图象是（ ）
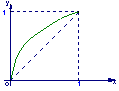
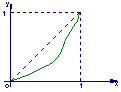
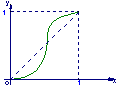
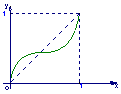
A B C D
二、填空题
1．在数列{an}中,a1=1,a2=2,且
则
=_____．
2．设等比数列{
}的公比为q，前n项和为
，若
，，
成等差数列，则q的值为
三、解答题
1．数列
的前n项和为S
,且
n=1,2,3….求
（I）
的值及数列的通项公式；
（II）
的值.
2．
已知
（Ⅰ）当
时，求数列
的前n项和
（Ⅱ）求
。
3．已知
是各项均为正数的等差数列，
、
、
成等差数列．又
，
…．
（Ⅰ）证明
为等比数列；
（Ⅱ）如果无穷等比数列各项的和
，求数列的首项和公差
．
（注：无穷数列各项的和即当
时数列前项和的极限）
4．设数列的首项
,且
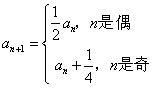,记
(Ⅰ)求
(Ⅱ)判断数列是否为等比数列,并证明你的结论;
(Ⅲ)求
5．设等比数列的公比为
，前n项和
（Ⅰ）求的取值范围；
（Ⅱ）设
，记
的前n项和为
，试比较与的大小
6．已知数列
（1）证明
（2）求数列的通项公式an.
7．在等差数列{an}中，公差d≠0,且a2是a1和a4的等比中项,已知a1,a3,
成等比数列，求数列k1,k2,k3,…,kn的通项kn