08届高中毕业班文科数学第三次质量检查
数学试题(文科)
考试时间:120分钟 试卷满分:150分
注意事项:
![]() 准考证号码填写说明:准考证号码共九位,每位都体现不同的分类,具体如下:
准考证号码填写说明:准考证号码共九位,每位都体现不同的分类,具体如下:
| 0 | 5 | 0 | 0 | 0 |
答题卡上科目栏内必须填涂考试科目
一、选择题(本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的,请将答案填入答题纸的相应位置,否则不给分)
1.已知直线![]() 平行,则a等于 ( )
平行,则a等于 ( )
A.1 B.-1 C.2 D.-1或2
2.若![]() 成立的 ( )
成立的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.过点![]() 的直线l经过圆
的直线l经过圆![]() 的圆心,则直线l的倾斜角大小为( )
的圆心,则直线l的倾斜角大小为( )
A.150° B.120° C.30° D.60°
4.已知集合![]() ,
,![]() ,且
,且![]() ,若
,若![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.设定点F1(0,-3)、F2(0,3),动点P满足条件![]() ,则点P的轨迹是 ( )
,则点P的轨迹是 ( )
A.椭圆 B.线段 C.不存在 D.椭圆或线段
6.若![]()
![]() ,则函数
,则函数![]() 与
与![]() 的图象 ( )
的图象 ( )
A.关于![]() 轴对称 B.关于
轴对称 B.关于![]() 轴对称
轴对称
C.关于直线![]() 对称
D.关于原点对称
对称
D.关于原点对称
7.设![]() 则
则![]() 等于 ( )
等于 ( )
A.213 B.212 C.26 D.27
8.椭圆![]() 和
和![]()
![]() 具有 ( )
具有 ( )
A.相同的离心率 B.相同的焦点
C.相同的顶点 D.相同的长、短轴
9.已知x、y满足约束条件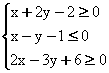 ,则
,则![]() 的最小值为 ( )
的最小值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
|
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.设![]() 的平均数,m是
的平均数,m是![]() 的平均数,n是
的平均数,n是![]() 的平均数,则下列各式正确的是 ( )
的平均数,则下列各式正确的是 ( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.已知![]() 是椭圆
是椭圆![]() 上的一点,若
上的一点,若![]() 到椭圆右准线的距离是
到椭圆右准线的距离是![]() ,则点
,则点![]() 到左焦点的距离是 ( )
到左焦点的距离是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:(本大题共4小题,每小题4分,共16分. 请将答案填入答题纸的相应位置,否则不给分)
13.已知Sn是数列{an}的前n项和,且Sn = 3n-2,则an = .
14.顶点在原点,坐标轴为对称轴的抛物线过点(-2,3),则它的方程是 .
15.如果实数x、y满足等式![]() ,则
,则![]() 最大值
最大值
16.下列命题中,
①![]() 的最小值是2 ;
②
的最小值是2 ;
②![]() 的最小值是
的最小值是![]() ;
;
③![]() 的最小值是2;④当x>0时,
的最小值是2;④当x>0时,![]() 的最小值是2,
的最小值是2,
⑤当x>1时,![]() 的最小值是2;
的最小值是2;
其正确命题的序号为
|
17.(本小题满分12分,每小题6分)
(1)求经过点![]() ,且与两坐标轴构成等腰三角形的直线方程.
,且与两坐标轴构成等腰三角形的直线方程.
(2)求满足(1)中条件的直线与y轴围成的三角形的外接圆的方程.
18.(本小题满分12分)
已知函数![]() 。
。
(1)写出函数的单调递减区间;
(2)设![]() ,f (x)的最小值是-2,最大值是
,f (x)的最小值是-2,最大值是![]() ,求实数a、b的值.
,求实数a、b的值.
19.(本小题满分12分)
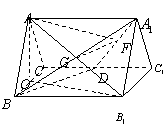
如图,正三棱柱![]() 的所有棱长都为
的所有棱长都为![]() ,
,![]() 为
为![]() 中点.
中点.
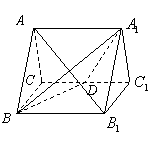 (Ⅰ)求证:
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
20.(本小题满分12分)
已知圆C圆心在x轴,且过两点A(-1,1),B![]()
(1)求圆C的方程
(2)设有点列![]() ,过点Pn(n=1,2……)引圆C的切线,若切线的斜率为kn,求和
,过点Pn(n=1,2……)引圆C的切线,若切线的斜率为kn,求和![]()
21. (本小题满分14分)
已知两个函数![]() ,
,![]() .
.
(1)![]() ,解不等式
,解不等式![]()
(2)若对任意![]() [-3,3],都有
[-3,3],都有![]()
![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
22.(本小题满分12分)
已知平面内任意一点P满足PF1+PF2=10,其中F1(0,-4)、F2(0,4) 为平面内两个定点,
(1)求点P的轨迹方程.
(2)若O为原点,Q是OP的中点,M在F2Q上,且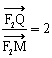 ,求点M的轨迹方程.
,求点M的轨迹方程.
参考答案
一、选择题(每小题5分,共60分):
|
二、填空题(每小题4分,共16分):
13.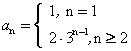 ; 14.
; 14.![]() 或
或![]() ; 15.
; 15. ![]() ;
16.①⑤.
;
16.①⑤.
三、解答题:
17.(12分) 解(1):设直线![]() 的方程为:
的方程为:![]() ……2分,
……2分,
又![]()
![]() 上,
上,![]() ……3分
……3分
由①②解得a=3,b=3或a=-1,b=1 ……5分
∴直线![]() 的方程为:x+y-3=0或x-y+1=0
……6分
的方程为:x+y-3=0或x-y+1=0
……6分
(2)因为(1)中所求得的两条直线互相垂直,所以y轴被两直线截得的线段即是所求圆的直径且经过P点.令圆心为(0,b),
又x+y-3=0和x-y+1=0在y轴截距分别为3和1, ……9分
则![]() =r2 , 得到b=2.
……11分
=r2 , 得到b=2.
……11分
所求圆的标准方程为![]() .
……12分
.
……12分
18.(12分)(1)解:![]()
![]() .……4分
.……4分
∵a>0,x∈R,∴f (x)的递减区间是![]() (k∈Z)……6分
(k∈Z)……6分
(2)解:∵x∈[0,![]() ],∴2x∈[0,
],∴2x∈[0,![]() ],2x-
],2x-![]() ∈[
∈[![]() ] …….8分
] …….8分
∴![]() ……9分 ∴函数f (x)的
……9分 ∴函数f (x)的
最小值是![]() ,最大值是
,最大值是![]()
由已知得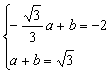 ,……11分. 解得a=2,b=
,……11分. 解得a=2,b=![]() ……12分
……12分
19.
(12分)解法一:(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]() .
.
![]() 为正三角形,
为正三角形,![]() .
.
![]() 正三棱柱
正三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
 连结
连结![]() ,在正方形
,在正方形![]() 中,
中,![]() 分别为
分别为![]() 的中点,
的中点,
![]() ,
,
![]() .在正方形
.在正方形![]() 中,
中,
![]() ,
,
![]() 平面
平面![]() .
.
(Ⅱ)设![]() 与
与![]() 交于点
交于点![]() ,在平面
,在平面![]() 中,
中,
作![]() 于
于![]() ,连结
,连结![]() ,
,
由(Ⅰ)得![]() 平面
平面![]() .
.![]() ,
,
![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,由等面积法可求得
中,由等面积法可求得![]() ,
,
 又
又![]() ,
,
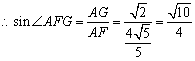 .
.
所以二面角![]() 的大小为
的大小为![]() .
.
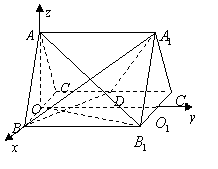
解法二:(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]() .
.
![]() 为正三角形,
为正三角形,![]() .
.
![]() 在正三棱柱
在正三棱柱![]() 中,
中,
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
取![]() 中点
中点![]() ,以
,以![]() 为原点,
为原点,![]() ,
,
![]() ,
,![]() 的方向为
的方向为![]() 轴的正方向建立空间直角坐标系, ……2分
轴的正方向建立空间直角坐标系, ……2分
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() , ……4分
, ……4分
![]() ,
,![]() .
.![]() 平面
平面![]() . ……5分
. ……5分
(Ⅱ)设平面![]() 的法向量为
的法向量为![]() . ……6分
. ……6分
![]() ,
,![]() .
.![]() ,
,![]() ,
,
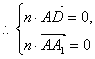
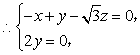
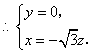 ……8分
……8分
令![]() 得
得![]() 为平面
为平面![]() 的一个法向量. …….9分
的一个法向量. …….9分
由(Ⅰ)知![]() 平面
平面![]() ,
,
![]() 为平面
为平面![]() 的法向量.……10分
的法向量.……10分
![]() ,
,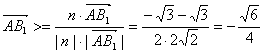 ……11分
……11分
![]() 二面角
二面角![]() 的大小为
的大小为![]() . ……12分
. ……12分
20.(12分)(1)设圆C方程![]() 代入A、B两点坐标,得
代入A、B两点坐标,得
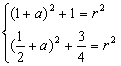 解得
解得 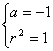
∴圆C:![]() ……5分
……5分
(2)设过点Pn(n,0)的圆C的切线方程为 ![]() ……6分
……6分
即 ![]() 又圆心C(-1,0)到切线距离等于圆的半径
又圆心C(-1,0)到切线距离等于圆的半径
∴![]() ……8分 即
……8分 即![]()
解得![]() ……9分; 又可变形为:
……9分; 又可变形为:![]() …… 10分
…… 10分
![]()
![]() 12分
12分
21![]() (14分)(1)设函数
(14分)(1)设函数![]() 的图象上任一点
的图象上任一点![]() 关于原点的对称点为
关于原点的对称点为![]() ,
,
则 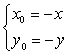 .
.
∵点![]() 在函数
在函数![]() 的图象上.
的图象上.
![]()
![]() 即
即![]() 故
故![]()
![]()
由![]() 可得:
可得:![]()
当![]() 时,
时,![]() ,此时不等式无解
,此时不等式无解 ![]()
当![]()
![]()
![]() 时,
时,![]() ,
,![]()
![]()
因此,原不等式的解集为![]() .
.![]()
(另解:![]() 得
得![]()
![]()
![]() ,因此,原不等式的解集为
,因此,原不等式的解集为![]() )
)
(2)依题意:![]()
![]()

列表(略)

22.(12分)解:(1)已知PF1+PF2=10>F1F2=8,所以P点的轨迹是以2a=10为长轴,以F1、F2为焦点,而且焦点在y轴上的椭圆…..2分
即:a=5,c=4,
则b=3. 所以P点的轨迹方程为![]() ……4分
……4分
(2)令M(x,y),Q(x1,y1),P(xo,yo),由已知M也为F2Q中点……5分
则有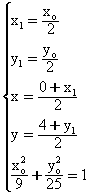 ……9分;
……9分;
得方程为![]() ……11分
……11分
故点M轨迹方程为![]() …….12分
…….12分