高考数学复习推理与证明变式题
一、合情推理
1.人教A版选修2-2第79页例1:已知数列![]() 的第1项
的第1项![]() ,且
,且![]()
![]() ,试归纳出这个数列的通项公式.
,试归纳出这个数列的通项公式.
变式1:已知数列![]() 的第1项
的第1项![]() ,且
,且![]()
![]() ,试归纳出这个数列的通项公式.
,试归纳出这个数列的通项公式.
解:![]() ,
,![]() ,…,一般地有
,…,一般地有![]() ;
;
本题也可以直接求出通项公式.
由![]() 得,
得,![]() ,即
,即![]() ,
,
所以数列![]() 是首项为
是首项为![]() ,公差为2的等差数列,则
,公差为2的等差数列,则![]() ,
,
而![]() ,则
,则![]() .
.
理科学生还可以先归纳,提出猜想,然后用数学归纳法证明.
变式2:已知数列![]() 的第1项
的第1项![]() ,且
,且![]()
![]() ,试归纳出这个数列的通项公式.
,试归纳出这个数列的通项公式.
解:![]() ,
,![]() ,…,一般地有
,…,一般地有![]() ;
;
本题也可以直接求出通项公式.
由![]() 得,
得,![]() ,即
,即![]() ,
,
所以数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,则
的等差数列,则![]() ,
,
而![]() ,则
,则![]() .
.
由变式(1)、变式(2)你能总结出什么规律?
对满足![]()
![]() 型的数列
型的数列![]() ,当
,当![]() 时采取取倒数的方法即可得出数列
时采取取倒数的方法即可得出数列![]() 是等差数列,再根据等差数列的通项公式即可求出数列
是等差数列,再根据等差数列的通项公式即可求出数列![]() 的通项.
的通项.
变式3:(2005年高考湖南卷)已知数列![]() 的第1项
的第1项![]() ,且
,且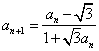
![]() ,则
,则![]()
A.0
B.![]() C.
C.![]() D.
D.![]()
解法1:由于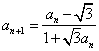 ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,由此归纳出数列
,由此归纳出数列![]() 是以3为周期的数列,则
是以3为周期的数列,则![]() ,选B.
,选B.
解法2: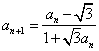 ,令
,令![]() ,则
,则![]() ,
,
则![]() ,即
,即![]() ,
,![]() ,
,
而![]() ,则
,则![]() ,
,![]() ;
;
变式4:(2007年广州市高考二模)已知数列![]() 满足
满足![]() ,
,![]() (
(![]() ),则
),则![]() 的值为
,
的值为
, ![]() 的值为
.
的值为
.
【思路1】分别求出![]() 、
、![]() 、
、![]() 、
、![]() ,可以发现
,可以发现![]() ,且
,且![]() ,故
,故![]()
![]() .
.
【思路2】由![]() ,联想到两角和的正切公式,设
,联想到两角和的正切公式,设![]() ,则有
,则有![]() ,
,![]() ,
,![]() ,
,![]() ,…….
,…….
则![]() ,故
,故![]()
![]() .
.
从以上变式3到变式5,你能受到什么启发呢?结构与两角和或差正切公式相似,这样的数列一定是周期数列.
2.人教A版选修2-2第83页例3:类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.
变式1:直角三角形与直角四面体的性质类比
| 平面内直角三角形的性质 | 空间中直角四面体的性质 |
|
在ΔABC中,∠BCA=900,点C在AB上的射影为D,则有下列结论: (1) 点D在线段AB上. (2) AB>AC,AB>BC, 即直角三角形三边中斜边最长. (3) 射影定理: AC2=ADAB, CB2=DBAB, CD2=ADDB (4) |
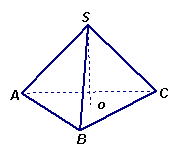
在四面体SABC中,三个平面SAB、平面SBC、平面SAC两两垂直,点S在底面上的射影为O,则有类似结论: (1) 点O在ΔABC内. (2) ΔABC,ΔABS,ΔSBC,ΔASC中,ΔABC的面积最大; (3)
(4) |
 以上结论的证明如下:
以上结论的证明如下:
(1)由题设SA,SB,SC两两垂直,则三角形SBC为直角三角形,则斜边BC边上的高SD在三角形SBC内,即点D在BC上,
连结AD,则BC⊥平面SAD,则平面ABC⊥平面ASD,过点S在面SAD内作SO![]() AD于O,则SO⊥平面ABC,即点S在平面ABC的射影为O;
AD于O,则SO⊥平面ABC,即点S在平面ABC的射影为O;
由于三角形SAD为直角三角形,则斜边AD上的高的垂足O在线段AD上,即O在三角形ABC内.
(2)由于![]() ,
,![]() ,
,
∵SAD为直角三角形,则斜边![]() ,故
,故![]() ;
;
同理可证:![]() ,
,![]() .
.
(3)![]() ,而在直角三角形ASD中,
,而在直角三角形ASD中,![]() ,
,
∴![]() ,
,
因此 ![]() .,同理可证
.,同理可证![]() ,
,![]() .
.
(4)在直角三角形SAD中,由于SO![]() AD于O,则
AD于O,则![]() ,
,
在直角三角形SBC中,由于SD![]() BC于D,则
BC于D,则![]() ,
,
因此![]() .
.
变式2:平面内的一般三角形与空间中的四面体性质类比
| 三角形 | 四面体 |
| 三角形两边之和大于第三边. | 四面体任意三个面的面积之和大于第四个面的面积. |
| 三角形的三条内角平分线交于一点且该点是三角形内切圆的圆心. | 四面体的六个二面角的平分面交于一点,且该点是四面体内切球的球心. |
| 三角形任意两边中点的连线平行于第三边,且等于第三边的一半. | 四面体任意三条棱的中点连成的三角形的面积等于第四个面面积的 |
| 三角形的任何一条边上的中线将三角形分成面积相等的两部分. | 四面体的任何一个三角形面上的一条中线和这个三角形所在平面外一顶点所确定的平面将这个四面体分成体积相等的两部分. |
| 三角形的三条中线交于一点,且三角形的每一条中线被该点分成的两段的比为2:1. | 将四面体的每一个顶点和对面的重心相连接,所得四条线段交于一点,且其中每一条线段被交点分成的两段的比都是3:1 |
| 在ΔABC中, | 在四面体ABCD中,二面角C-AB-D的平分面交棱CD于点E,则, |
| 在ΔABC中, | 在四面体ABCD中,棱AB与面ACD、BCD的夹角分别 |
| 设ΔABC的三边长分别为 (1) (2) | 四面体S—ABCD的四个侧面的面积分别为 (2) |
以上性质,限于篇幅,不再一一证明.
变式3:平面内三角形与空间中的三棱柱性质类比
| 三角形 | 三棱柱 |
| 三角形的三个内角之和为180 | 三棱柱的任意两个侧面所成的三个二面角之和为180 |
| 三角形中任意两个两边之和大于第三边 | 三棱柱的任意两个侧面的面积之和大于第三个侧面的面积 |
| 三角形中较大的边所对的角较大;反之,较大的角所对的边也较大. | 三棱柱中面积较大的侧面所对的二面角较大;反之,较大的二面角所对的侧面的面积也较大. |
| 三角形中位线定理:三角形任意两边中点的连线平行于第三边,且等于第三边的一半. | 经过三棱柱ABC-A1B1C1的棱A1C1、B1C1、BC中点D、E、F的平面与侧面A1B1BA平行,且该平面被三棱柱ABC-A1B1C1所截得的四边形DEFG的面积是侧面A1B1BA面积的
|
| 三角形内角平分线定理: 在ΔABC中, 则 |
|
| 正弦定理: 在ΔABC中,有 | 如图,在三棱柱ABC—A1B1C1中,二面角B—AA1—C、C—BB1—A、B—CC1—A所成的二面角分别为
|
| 余弦定理:在ΔABC中,有
| 在三棱柱ABC—A1B1C1中,二面角B—AA1—C、C—BB1—A、B—CC1—A所成的二面角分别为
|
| 三角形的面积为 | 在三棱柱ABC—A1B1C1中,棱CC1到侧面A1ABB1的距离为 |
 以上性质证明的关键是构造直截面(与侧棱垂直的截面),转化为平面问题,以正弦定理的拓广为例,其余的类似证明.
以上性质证明的关键是构造直截面(与侧棱垂直的截面),转化为平面问题,以正弦定理的拓广为例,其余的类似证明.
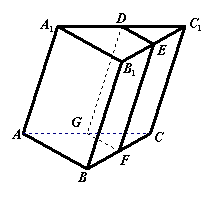
(6)如图4,在三棱柱ABC—A1B1C1中,二面角B—AA1—C、
C—BB1—A、B—CC1—A所成的二面角分别为![]() 、
、![]() 、
、![]() ,
,
则 ![]() ;
;
证明:作平面DEF与三棱柱ABC-A1B1C1侧棱垂直,分别交侧棱AA1,BB1 ,CC1于点D,E,F,则![]() =
=![]() ,
,![]() ,
,![]() ,
,
在![]() DEF中,根据正弦定理得
DEF中,根据正弦定理得![]() ,即
,即![]()
而![]() ,且
,且![]() ,因此
,因此![]() .
.
二、直接证明与间接证明
1.人教A版选修2-2第96页例1 在ΔABC中,三个内角A,B,C对应的边分别为![]() ,且A,B,C成等差数列,
,且A,B,C成等差数列,![]() 成等比数列,求证ΔABC为等边三角形.
成等比数列,求证ΔABC为等边三角形.
变式1:在ΔABC中,三个内角A,B,C对应的边分别为![]() ,且A,B,C成等差数列,
,且A,B,C成等差数列,![]() 也成等差数列,求证ΔABC为等边三角形.
也成等差数列,求证ΔABC为等边三角形.
证明:由A,B,C成等差数列知,![]() ,由余弦定理知
,由余弦定理知![]() ,
,
又![]() 也成等差数列,∴
也成等差数列,∴![]() ,代入上式得
,代入上式得![]() ,
,
整理得![]() ,∴
,∴![]() ,从而
,从而![]() ,而
,而![]() ,则
,则![]() ,
,
从而ΔABC为等边三角形.
变式2:在ΔABC中,三个内角A,B,C对应的边分别为![]() ,且
,且![]() 成等比数列,
成等比数列,![]() 成等差数列,求证ΔABC为等边三角形.
成等差数列,求证ΔABC为等边三角形.
证明:由于![]() 成等比数列,则
成等比数列,则![]() ,即
,即![]() ∴
∴![]() (1)
(1)
又![]() 成等差数列,则
成等差数列,则![]()
则![]() ,
,
由于![]() ,∴
,∴![]() ,即
,即![]() (2)
(2)
将(2)式代入(1)式得:![]() ,
,
∴![]() 或
或![]() (舍去),而
(舍去),而![]() ,∴
,∴![]() (3)
(3)
将(3)代入(1)得:![]() ,由于
,由于![]() ,∴
,∴![]() ,
,
因此![]() ,从而ΔABC为等边三角形.
,从而ΔABC为等边三角形.
变式3:在ΔABC中,三个内角A,B,C对应的边分别为![]() ,且
,且![]() 成等比数列,
成等比数列,![]() 成等比数列,求证ΔABC为等边三角形.
成等比数列,求证ΔABC为等边三角形.
证明:由于![]() 成等比数列,则
成等比数列,则![]() ,即
,即![]() ∴
∴![]() (1)
(1)
又![]() 成等比数列,则
成等比数列,则![]() ,∴
,∴![]() ,
,
即![]() (2)
(2)
将(2)代入(1)得:![]() ,∴
,∴![]() 或
或![]() (舍去)
(舍去)
而![]() ,∴
,∴![]() (3)将(3)代入(1)得:
(3)将(3)代入(1)得:![]() ,
,
由于![]() ,∴
,∴![]() ,因此
,因此![]() ,从而ΔABC为等边三角形.
,从而ΔABC为等边三角形.
变式4:在ΔABC中,三个内角A,B,C对应的边分别为![]() ,且
,且![]() 成等差数列,
成等差数列,![]() 成等差数列,求证ΔABC为等边三角形.
成等差数列,求证ΔABC为等边三角形.
证明:由于![]() 成等差数列,则
成等差数列,则![]() =
=![]()
∴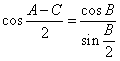 (1)
(1)
又![]() 成等差数列,则
成等差数列,则![]() ,∴
,∴![]() ,
,
由于![]() ,∴
,∴![]() (2)
(2)
将(1)代入(2)得![]() ,∴
,∴![]() ,而
,而![]() ,∴
,∴![]() (3)将(3)代入(2)得:
(3)将(3)代入(2)得:![]() ,由于
,由于![]() ,∴
,∴![]() ,
,
因此![]() ,从而ΔABC为等边三角形.
,从而ΔABC为等边三角形.
变式5: 在ΔABC中,三个内角A,B,C对应的边分别为![]() ,且
,且![]() 成等差数列,
成等差数列,![]() 成等比数列,求证ΔABC为等边三角形.
成等比数列,求证ΔABC为等边三角形.
证明:由于![]() 成等差数列,则
成等差数列,则![]() =
=![]()
∴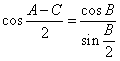 ,则
,则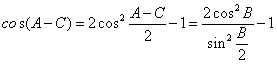 (1)
(1)
又![]() 成等比数列,则
成等比数列,则![]() ,∴
,∴![]() ,
,
即![]() (2)
(2)
将(1)代入(2)整理得:![]()
即![]() ,分解因式得
,分解因式得
![]() ,∴
,∴![]() 或
或![]() (舍去)或
(舍去)或![]() (舍去)
(舍去)
而![]() ,∴
,∴![]() (3)将(3)代入(2)得:
(3)将(3)代入(2)得:![]() ,
,
由于![]() ,∴
,∴![]() ,因此
,因此![]() ,从而ΔABC为等边三角形.
,从而ΔABC为等边三角形.
2.人教A版选修2-2第101页例5:求证![]() 是无理数
是无理数
变式1:求证![]() 是无理数
是无理数
证明:假设![]() 是无理数,则存在互质的数
是无理数,则存在互质的数![]() ,使得
,使得![]() ,从而
,从而 ![]() ,即
,即![]() ,
,
所以![]() 为3的倍数,于是可设
为3的倍数,于是可设![]() ,因此,
,因此,![]() ,即
,即![]() ,所以
,所以![]() 也为3的倍数,这与
也为3的倍数,这与![]() 互质矛盾,由此可知假设是错误的,从而
互质矛盾,由此可知假设是错误的,从而![]() 是无理数.
是无理数.
变式2:若![]() 为奇数,则
为奇数,则![]() 是无理数.
是无理数.
证明:假设![]() 是有理数,则存在互质的数
是有理数,则存在互质的数![]() ,使得
,使得![]() ,则
,则
![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() 为偶数,
为偶数,
由于![]() 为偶数,说明,
为偶数,说明,![]() 与
与![]() 同为偶数或同为奇数,由于它们的积为偶数,则
同为偶数或同为奇数,由于它们的积为偶数,则![]() 与
与![]() 同为偶数,设
同为偶数,设![]() ,
,![]()
![]() ,从而有
,从而有![]()
即![]() ,∴
,∴![]() 为偶数,∴
为偶数,∴![]() 为偶数,则
为偶数,则![]() 也为偶数,这与
也为偶数,这与![]() 互质矛盾,由此可知假设是错误的,从而
互质矛盾,由此可知假设是错误的,从而![]() 是无理数.
是无理数.
三、数学归纳法
人教A版选修2-2第106页例1:用数学归纳法证明 ![]() .
.
变式1:是否存在常数![]() ,使得
,使得![]() 对一切正整数
对一切正整数![]() 都成立?并证明你的结论.
都成立?并证明你的结论.
解:假设存在常数![]() 使等式成立,令
使等式成立,令![]() 得:
得: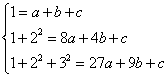 解之得
解之得![]() ,下面用数学归纳法证明:
,下面用数学归纳法证明:![]() 对一切正整数
对一切正整数![]() 都成立.(略)
都成立.(略)
变式2:已知![]() ,是否存在
,是否存在![]() 的整式
的整式![]() ,使得等式
,使得等式![]() 对于大于1的一切正整数
对于大于1的一切正整数![]() 都成立?并证明你的结论.
都成立?并证明你的结论.
解:假设![]() 存在,
存在,
令![]() ,求得
,求得![]() ,令
,令![]() ,求得
,求得![]() ,令
,令![]() ,求得
,求得![]() ,
,
由此猜想:![]() ,下面用数学归纳法证明:
,下面用数学归纳法证明:![]() 对一切大于1的正整数
对一切大于1的正整数![]() 都成立.(略)
都成立.(略)

 在三棱柱ABC-A1B1C1中,平面BB1GH平分面角A—BB1—C1,则
在三棱柱ABC-A1B1C1中,平面BB1GH平分面角A—BB1—C1,则