高考数学数列试题汇编
重庆文1
在等比数列{an}中,a2=8,a5=64,,则公比q为( A )
A.2 B.3 C.4 D.8
重庆理1
若等差数列{![]() }的前三项和
}的前三项和![]() 且
且![]() ,则
,则![]() 等于( A )
等于( A )
A.3 B.4 C.5 D.6
安徽文3
等差数列![]() 的前
的前![]() 项和为
项和为![]() 若
若![]() ( B )
( B )
A.12 B.10 C.8 D.6
辽宁文5
设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,
,![]() ,则
,则![]() ( B )
( B )
A.63 B.45 C.36 D.27
福建文2
等比数列![]() 中,
中,![]() ,则
,则![]() 等于( C )
等于( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
福建理2
数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则
,则![]() 等于( B )
等于( B )
A.1 B.![]() C.
C.![]() D.
D.![]()
广东理5
已知数列{![]() }的前
}的前![]() 项和
项和![]() ,第
,第![]() 项满足
项满足![]() ,则
,则![]() ( B )
( B )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
湖北理5
已知![]() 和
和![]() 是两个不相等的正整数,且
是两个不相等的正整数,且![]() ,则
,则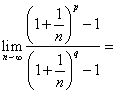 ( C )
( C )
A.0 B.1 C.![]() D.
D.![]()
湖南文4
在等比数列![]() (
(![]() )中,若
)中,若![]() ,
,![]() ,则该数列的前10项和为( B )
,则该数列的前10项和为( B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
湖北理8
已知两个等差数列![]() 和
和![]() 的前
的前![]() 项和分别为A
项和分别为A![]() 和
和![]() ,且
,且![]() ,则使得
,则使得![]() 为整数的正整数
为整数的正整数![]() 的个数是( D )
的个数是( D )
A.2 B.3 C.4 D.5
湖南理10
设集合![]() ,
, ![]() 都是
都是![]() 的含两个元素的子集,且满足:对任意的
的含两个元素的子集,且满足:对任意的![]() ,
,![]() (
(![]() ,
,![]() ),都有
),都有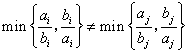 (
(![]() 表示两个数
表示两个数![]() 中的较小者),则
中的较小者),则![]() 的最大值是( B )
的最大值是( B )
A.10 B.11 C.12 D.13
辽宁理4
设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,
,![]() ,则
,则![]() ( )
( )
A.63 B.45 C.36 D.27
宁夏文6
已知![]() 成等比数列,且曲线
成等比数列,且曲线![]() 的顶点是
的顶点是![]() ,则
,则![]() 等于( B )
等于( B )
A.3 B.2 C.1 D.![]()
宁夏理4
已知![]() 是等差数列,
是等差数列,![]() ,其前10项和
,其前10项和![]() ,则其公差
,则其公差![]() ( D )
( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
陕西文5
等差数列{an}的前n项和为Sn,若![]() ( C )
( C )
A.12 B.18 C.24 D.42
四川文7
等差数列{an}中,a1=1,a3+a5=14,其前n项和Sn=100,则n=( B )
A.9 B.10 C.11 D.12
上海文14
数列![]() 中,
中,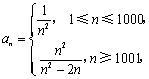 则数列
则数列![]() 的极限值( B )
的极限值( B )
A.等于![]() B.等于
B.等于![]() C.等于
C.等于![]() 或
或![]() D.不存在
D.不存在
陕西理5
各项均为正数的等比数列![]() 的前n项和为Sn,若Sn=2,S30=14,则S40等于( C )
的前n项和为Sn,若Sn=2,S30=14,则S40等于( C )
A.80 B.30 C.26 D.16
天津理8
设等差数列![]() 的公差
的公差![]() 不为0,
不为0,![]() .若
.若![]() 是
是![]() 与
与![]() 的等比中项,则
的等比中项,则![]() ( B )
( B )
A.2 B.4 C.6 D.8
重庆理14
设{![]() }为公比q>1的等比数列,若
}为公比q>1的等比数列,若![]() 和
和![]() 是方程
是方程![]() 的两根,则
的两根,则![]() _____.18
_____.18
天津理13
设等差数列![]() 的公差
的公差![]() 是2,前
是2,前![]() 项的和为
项的和为![]() ,则
,则![]() .3
.3
全国2文14
已知数列的通项![]() ,则其前
,则其前![]() 项和
项和![]() .
.![]()
全国1理15
等比数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() ,
,![]() ,
,![]() 成等差数列,则
成等差数列,则![]() 的公比为 .
的公比为 .![]()
宁夏文16
已知![]() 是等差数列,
是等差数列,![]() ,其前5项和
,其前5项和![]() ,则其公差
,则其公差![]() .
.![]()
江西理14
已知数列![]() 对于任意
对于任意![]() ,有
,有![]() ,若
,若![]() ,则
,则![]() .4
.4
江西文14
已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则
,则![]() .7
.7
广东文13
已知数列{![]() }的前
}的前![]() 项和
项和![]() ,则其通项
,则其通项![]() ;若它的第
;若它的第![]() 项满足
项满足![]() ,则
,则![]() . 2n-10 ;
8
. 2n-10 ;
8
北京理10
若数列![]() 的前
的前![]() 项和
项和![]() ,则此数列的通项公式为 ;数列
,则此数列的通项公式为 ;数列![]() 中数值最小的项是第 项.
中数值最小的项是第 项.![]()
![]()
北京文10
若数列![]() 的前
的前![]() 项和
项和![]() ,则此数列的通项公式为 .
,则此数列的通项公式为 .![]()
重庆理21
已知各项均为正数的数列{![]() }的前n项和满足
}的前n项和满足![]() ,且
,且![]()
(1)求{![]() }的通项公式;
}的通项公式;
(2)设数列{![]() }满足
}满足![]() ,并记
,并记![]() 为{
为{![]() }的前n项和,求证:
}的前n项和,求证:
![]()
(Ⅰ)解:由![]() ,解得a1=1或a1=2,由假设a1=S1>1,因此a1=2。
,解得a1=1或a1=2,由假设a1=S1>1,因此a1=2。
又由an+1=Sn+1- Sn=![]() ,
,
得an+1- an-3=0或an+1=-an
因an>0,故an+1=-an不成立,舍去。
因此an+1- an-3=0。从而{an}是公差为3,首项为2的等差数列,故{an}的通项为an=3n-2。
(Ⅱ)证法一:由![]() 可解得
可解得
![]() ;
;
从而![]() 。
。
因此![]() 。
。
令![]() ,则
,则
![]() 。
。
因![]() ,故
,故
![]() .
.
特别的![]() 。从而
。从而![]() ,
,
即![]() 。
。
证法二:同证法一求得bn及Tn。
由二项式定理知当c>0时,不等式
![]() 成立。
成立。
由此不等式有
![]()
![]()
=![]() 。
。
证法三:同证法一求得bn及Tn。
令An=![]() ,Bn=
,Bn=![]() ,Cn=
,Cn=![]() 。
。
因![]() ,因此
,因此![]() 。
。
从而
![]()
>![]() 。
。
浙江理21
已知数列![]() 中的相邻两项
中的相邻两项![]() 是关于
是关于![]() 的方程
的方程![]() 的两个根,且
的两个根,且![]() .
.
(I)求![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(II)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)记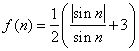 ,
,
![]() ,
,
求证:![]() .
.
本题主要考查等差、等比数列的基本知识,考查运算及推理能力.满分15分.
(I)解:方程![]() 的两个根为
的两个根为![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,
所以![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 时;
时;
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() .
.
(II)解:![]()
![]()
![]() .
.
(III)证明:![]() ,
,
所以![]() ,
,
![]() .
.
当![]() 时,
时,
![]() ,
,
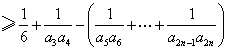
![]()
![]() ,
,
同时,![]()
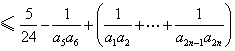
![]()
![]() .
.
综上,当![]() 时,
时,![]() .
.
浙江文19
已知数列{![]() }中的相邻两项
}中的相邻两项![]() 、
、![]() 是关于x的方程
是关于x的方程![]() 的两个根,且
的两个根,且![]() ≤
≤![]() (k =1,2,3,…).
(k =1,2,3,…).
(I)求![]() 及
及![]() (n≥4)(不必证明);
(n≥4)(不必证明);
(Ⅱ)求数列{![]() }的前2n项和S2n.
}的前2n项和S2n.
本题主要考查等差、等比数列的基本知识,考查运算及推理能力.满分14分.
(I)解:方程![]() 的两个根为
的两个根为![]() .
.
当k=1时,![]() ,所以
,所以![]() ;
;
当k=2时,![]() ,所以
,所以![]() ;
;
当k=3时,![]() ,所以
,所以![]() ;
;
当k=4时,![]() ,所以
,所以![]() ;
;
因为n≥4时,![]() ,所以
,所以![]()
(Ⅱ)![]() =
=![]() .
.
天津理21
在数列![]() 中,
中,![]() ,其中
,其中![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)证明存在![]() ,使得
,使得![]() 对任意
对任意![]() 均成立.
均成立.
本小题以数列的递推关系式为载体,主要考查等比数列的前![]() 项和公式、数列求和、不等式的证明等基础知识与基本方法,考查归纳、推理、运算及灵活运用数学知识分析问题和解决问题的能力.满分14分.
项和公式、数列求和、不等式的证明等基础知识与基本方法,考查归纳、推理、运算及灵活运用数学知识分析问题和解决问题的能力.满分14分.
(Ⅰ)解法一:![]() ,
,
![]() ,
,
![]() .
.
由此可猜想出数列![]() 的通项公式为
的通项公式为![]() .
.
以下用数学归纳法证明.
(1)当![]() 时,
时,![]() ,等式成立.
,等式成立.
(2)假设当![]() 时等式成立,即
时等式成立,即![]() ,
,
那么![]()
![]()
![]() .
.
这就是说,当![]() 时等式也成立.根据(1)和(2)可知,等式
时等式也成立.根据(1)和(2)可知,等式![]() 对任何
对任何![]() 都成立.
都成立.
解法二:由![]() ,
,![]() ,
,
可得![]() ,
,
所以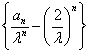 为等差数列,其公差为1,首项为0,故
为等差数列,其公差为1,首项为0,故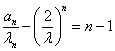 ,所以数列
,所以数列![]() 的通项公式为
的通项公式为![]() .
.
(Ⅱ)解:设![]() , ①
, ①
![]() ②
②
当![]() 时,①式减去②式,
时,①式减去②式,
得![]() ,
,
![]() .
.
这时数列![]() 的前
的前![]() 项和
项和![]() .
.
当![]() 时,
时,![]() .这时数列
.这时数列![]() 的前
的前![]() 项和
项和![]() .
.
(Ⅲ)证明:通过分析,推测数列![]() 的第一项
的第一项![]() 最大,下面证明:
最大,下面证明:
![]() . ③
. ③
由![]() 知
知![]() ,要使③式成立,只要
,要使③式成立,只要![]() ,
,
因为![]()
![]()
![]() .
.
所以③式成立.
因此,存在![]() ,使得
,使得![]() 对任意
对任意![]() 均成立.
均成立.
天津文20
在数列![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)证明数列![]() 是等比数列;
是等比数列;
(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)证明不等式![]() ,对任意
,对任意![]() 皆成立.
皆成立.
本小题以数列的递推关系式为载体,主要考查等比数列的概念、等比数列的通项公式及前![]() 项和公式、不等式的证明等基础知识,考查运算能力和推理论证能力.满分12分.
项和公式、不等式的证明等基础知识,考查运算能力和推理论证能力.满分12分.
(Ⅰ)证明:由题设![]() ,得
,得
![]() ,
,![]() .
.
又![]() ,所以数列
,所以数列![]() 是首项为
是首项为![]() ,且公比为
,且公比为![]() 的等比数列.
的等比数列.
(Ⅱ)解:由(Ⅰ)可知![]() ,于是数列
,于是数列![]() 的通项公式为
的通项公式为
![]() .
.
所以数列![]() 的前
的前![]() 项和
项和![]() .
.
(Ⅲ)证明:对任意的![]() ,
,
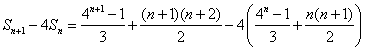
![]() .
.
所以不等式![]() ,对任意
,对任意![]() 皆成立.
皆成立.
四川文22
已知函数f(x)=x2-4,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,u)(u,N +),其中为正实数.
(Ⅰ)用xx表示xn+1;
(Ⅱ)若a1=4,记an=lg![]() ,证明数列{a1}成等比数列,并求数列{xn}的通项公式;
,证明数列{a1}成等比数列,并求数列{xn}的通项公式;
(Ⅲ)若x1=4,bn=xn-2,Tn是数列{bn}的前n项和,证明Tn<3.
解析:本题综合考查数列、函数、不等式、导数应用等知识,以及推理论证、计算及解决问题的能力.
(Ⅰ)由题可得![]() .
.
所以曲线![]() 在点
在点![]() 处的切线方程是:
处的切线方程是:![]() .
.
即![]() .
.
令![]() ,得
,得![]() .
.
即![]() .
.
显然![]() ,∴
,∴![]() .
.
(Ⅱ)由![]() ,知
,知![]() ,同理
,同理![]() .
.
故![]() .
.
从而![]() ,即
,即![]() .所以,数列
.所以,数列![]() 成等比数列.
成等比数列.
故![]() .
.
即![]() .
.
从而![]()
所以![]()
(Ⅲ)由(Ⅱ)知![]() ,
,
∴![]()
∴![]()
当![]() 时,显然
时,显然![]() .
.
当![]() 时,
时,![]()
∴![]()
![]()
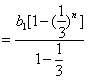
![]() .
.
综上,![]()
![]() .
.
上海理20
若有穷数列![]() (
(![]() 是正整数),满足
是正整数),满足![]() 即
即![]() (
(![]() 是正整数,且
是正整数,且![]() ),就称该数列为“对称数列”。
),就称该数列为“对称数列”。
(1)已知数列![]() 是项数为7的对称数列,且
是项数为7的对称数列,且![]() 成等差数列,
成等差数列,![]() ,试写出
,试写出![]() 的每一项
的每一项
(2)已知![]() 是项数为
是项数为![]() 的对称数列,且
的对称数列,且![]() 构成首项为50,公差为
构成首项为50,公差为![]() 的等差数列,数列
的等差数列,数列![]() 的前
的前![]() 项和为
项和为![]() ,则当
,则当![]() 为何值时,
为何值时,![]() 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)对于给定的正整数![]() ,试写出所有项数不超过
,试写出所有项数不超过![]() 的对称数列,使得
的对称数列,使得![]() 成为数列中的连续项;当
成为数列中的连续项;当![]() 时,试求其中一个数列的前2008项和
时,试求其中一个数列的前2008项和![]()
解:(1)设![]() 的公差为
的公差为![]() ,则
,则![]() ,解得
,解得 ![]() ,
,
![]() 数列
数列![]() 为
为![]() .
.
(2)![]()
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() 取得最大值.
取得最大值.
![]() 的最大值为626.
的最大值为626.
(3)所有可能的“对称数列”是:
① ![]() ;
;
② ![]() ;
;
③ ![]() ;
;
④ ![]() .
.
对于①,当![]() 时,
时,![]() .
.
当![]() 时,
时,![]()
![]()
![]() .
.
对于②,当![]() 时,
时,![]() .
.
当![]() 时,
时,![]()
![]() .
.
对于③,当![]() 时,
时,![]() .
.
当![]() 时,
时,![]()
![]() .
.
对于④,当![]() 时,
时,![]() .
.
当![]() 时,
时,![]()
![]() .
.
上海文20
如果有穷数列![]() (
(![]() 为正整数)满足条件
为正整数)满足条件![]() ,
,![]() ,…,
,…,![]() ,即
,即![]() (
(![]() ),我们称其为“对称数列”.
),我们称其为“对称数列”.
例如,数列![]() 与数列
与数列![]() 都是“对称数列”.
都是“对称数列”.
(1)设![]() 是7项的“对称数列”,其中
是7项的“对称数列”,其中![]() 是等差数列,且
是等差数列,且![]() ,
,![]() .依次写出
.依次写出![]() 的每一项;
的每一项;
(2)设![]() 是
是![]() 项的“对称数列”,其中
项的“对称数列”,其中![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,求
的等比数列,求![]() 各项的和
各项的和![]() ;
;
(3)设![]() 是
是![]() 项的“对称数列”,其中
项的“对称数列”,其中![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.求
的等差数列.求![]() 前
前![]() 项的和
项的和![]()
![]() .
.
解:(1)设数列![]() 的公差为
的公差为![]() ,则
,则![]() ,解得
,解得 ![]() ,
,
![]() 数列
数列![]() 为
为![]() .
.
(2)![]()
![]()
![]()
![]()
![]() .
.
(3)![]() .
.
由题意得 ![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.
的等差数列.
当![]() 时,
时,![]()
![]() .
.
当![]() 时,
时,![]()
![]()
![]()
![]() .
.
综上所述,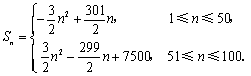
陕西理22
已知各项全不为零的数列{ak}的前k项和为Sk,且Sk=![]() N*),其中a1=1.
N*),其中a1=1.
(Ⅰ)求数列{ak}的通项公式;
(Ⅱ)对任意给定的正整数n(n≥2),数列{bk}满足![]() (k=1,2,…,n-1),b1=1.
(k=1,2,…,n-1),b1=1.
求b1+b2+…+bn.
解:(Ⅰ)当![]() ,由
,由![]() 及
及![]() ,得
,得![]() .
.
当![]() 时,由
时,由![]() ,得
,得![]() .
.
因为![]() ,所以
,所以![]() .从而
.从而![]() .
.
![]() ,
,![]() .故
.故![]() .
.
(Ⅱ)因为![]() ,所以
,所以![]() .
.
所以![]()
![]() .
.
故![]()
![]()
![]() .
.
陕西文20
已知实数列![]() 等比数列,其中
等比数列,其中![]() 成等差数列.
成等差数列.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)数列![]() 的前
的前![]() 项和记为
项和记为![]() 证明:
证明: ![]() <128
<128![]() …).
…).
解:(Ⅰ)设等比数列![]() 的公比为
的公比为![]() ,
,
由![]() ,得
,得![]() ,从而
,从而![]() ,
,![]() ,
,![]() .
.
因为![]() 成等差数列,所以
成等差数列,所以![]() ,
,
即![]() ,
,![]() .
.
所以![]() .故
.故![]() .
.
(Ⅱ)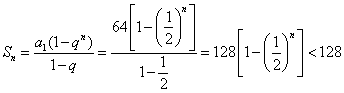 .
.
山东理17
设数列![]() 满足
满足![]() ,
,![]() .
.
(Ⅰ)求数列![]() 的通项;
的通项;
(Ⅱ)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
(I)![]()
![]()
![]()
![]()
验证![]() 时也满足上式,
时也满足上式,![]()
(II) ![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]()
山东文18
设![]() 是公比大于1的等比数列,
是公比大于1的等比数列,![]() 为数列
为数列![]() 的前
的前![]() 项和.已知
项和.已知![]() ,且
,且![]() 构成等差数列.
构成等差数列.
(1)求数列![]() 的等差数列.
的等差数列.
(2)令![]() 求数列
求数列![]() 的前
的前![]() 项和
项和![]() .
.
解:(1)由已知得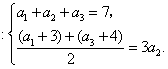
解得![]() .
.
设数列![]() 的公比为
的公比为![]() ,由
,由![]() ,可得
,可得![]() .
.
又![]() ,可知
,可知![]() ,
,
即![]() ,
,
解得![]() .
.
由题意得![]() .
.
![]() .
.
故数列![]() 的通项为
的通项为![]() .
.
(2)由于![]()
由(1)得![]()
![]()
又![]()
![]() 是等差数列.
是等差数列.
![]()
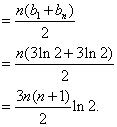
故![]() .
.
全国2理21
设数列![]() 的首项
的首项![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() ,证明
,证明![]() ,其中
,其中![]() 为正整数.
为正整数.
21.解:(1)由![]()
整理得 ![]() .
.
又![]() ,所以
,所以![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,得
的等比数列,得
![]()
(2)方法一:
由(1)可知![]() ,故
,故![]() .
.
那么,![]()
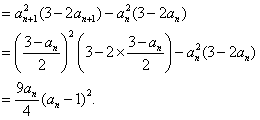
又由(1)知![]() 且
且![]() ,故
,故![]() ,
,
因此 ![]() 为正整数.
为正整数.
方法二:
由(1)可知![]() ,
,
因为![]() ,
,
所以 ![]() .
.
由![]() 可得
可得![]() ,
,
即 ![]()
两边开平方得 ![]() .
.
即 ![]() 为正整数.
为正整数.
全国2文17
设等比数列![]() 的公比
的公比![]() ,前
,前![]() 项和为
项和为![]() .已知
.已知![]() ,求
,求![]() 的通项公式.
的通项公式.
解:由题设知![]() ,
,
则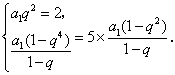 ②
②
由②得![]() ,
,![]() ,
,![]() ,
,
因为![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,代入①得
时,代入①得![]() ,通项公式
,通项公式![]() ;
;
当![]() 时,代入①得
时,代入①得![]() ,通项公式
,通项公式![]() .
.
全国1理22
已知数列![]() 中
中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 中
中![]() ,
,![]() ,
,![]() ,
,
证明:![]() ,
,![]() .
.
解:(Ⅰ)由题设:
![]()
![]()
![]() ,
,
![]() .
.
所以,数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
![]() ,
,
即![]() 的通项公式为
的通项公式为![]() ,
,![]() .
.
(Ⅱ)用数学归纳法证明.
(ⅰ)当![]() 时,因
时,因![]() ,
,![]() ,所以
,所以
![]() ,结论成立.
,结论成立.
(ⅱ)假设当![]() 时,结论成立,即
时,结论成立,即![]() ,
,
也即![]() .
.
当![]() 时,
时,
![]()
![]()
![]() ,
,
又![]() ,
,
所以 ![]()
![]()
![]()
![]() .
.
也就是说,当![]() 时,结论成立.
时,结论成立.
根据(ⅰ)和(ⅱ)知![]() ,
,![]() .
.
全国1文21
设![]() 是等差数列,
是等差数列,![]() 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且![]() ,
,![]() ,
,![]()
(Ⅰ)求![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅱ)求数列![]() 的前n项和
的前n项和![]() .
.
解:(Ⅰ)设![]() 的公差为
的公差为![]() ,
,![]() 的公比为
的公比为![]() ,则依题意有
,则依题意有![]() 且
且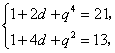
解得![]() ,
,![]() .
.
所以![]() ,
,
![]() .
.
(Ⅱ)![]() .
.
![]() ,①
,①
![]() ,②
,②
②-①得![]() ,
,
![]()
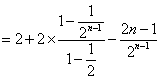
![]() .
.
辽宁理21
已知数列![]() ,
,![]() 与函数
与函数![]() ,
,![]() ,
,![]() 满足条件:
满足条件:
![]() ,
,![]() .
.
(I)若![]() ,
,![]() ,
,![]() ,
,![]() 存在,求
存在,求![]() 的取值范围;
的取值范围;
(II)若函数![]() 为
为![]() 上的增函数,
上的增函数,![]() ,
,![]() ,
,![]() ,证明对任意
,证明对任意![]() ,
,![]() (用
(用![]() 表示).
表示).
江西理22
设正整数数列![]() 满足:
满足:![]() ,且对于任何
,且对于任何![]() ,有
,有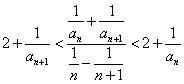 .
.
(1)求![]() ,
,![]() ;
;
(3)求数列![]() 的通项
的通项![]() .
.
解:(1)据条件得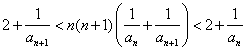 ①
①
当![]() 时,由
时,由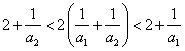 ,即有
,即有![]() ,
,
解得![]() .因为
.因为![]() 为正整数,故
为正整数,故![]() .
.
当![]() 时,由
时,由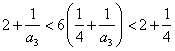 ,
,
解得![]() ,所以
,所以![]() .
.
(2)方法一:由![]() ,
,![]() ,
,![]() ,猜想:
,猜想:![]() .
.
下面用数学归纳法证明.
1![]() 当
当![]() ,
,![]() 时,由(1)知
时,由(1)知![]() 均成立;
均成立;
2![]() 假设
假设![]() 成立,则
成立,则![]() ,则
,则![]() 时
时
由①得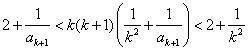
![]()
![]()
因为![]() 时,
时,![]() ,所以
,所以![]() .
.
![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() .
.
故![]() ,即
,即![]() 时,
时,![]() 成立.
成立.
由1![]() ,2
,2![]() 知,对任意
知,对任意![]() ,
,![]() .
.
(2)方法二:
由![]() ,
,![]() ,
,![]() ,猜想:
,猜想:![]() .
.
下面用数学归纳法证明.
1![]() 当
当![]() ,
,![]() 时,由(1)知
时,由(1)知![]() 均成立;
均成立;
2![]() 假设
假设![]() 成立,则
成立,则![]() ,则
,则![]() 时
时
由①得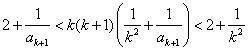
即![]() ②
②
由②左式,得![]() ,即
,即![]() ,因为两端为整数,
,因为两端为整数,
则![]() .于是
.于是![]() ③
③
又由②右式,![]() .
.
则![]() .
.
因为两端为正整数,则![]() ,
,
所以![]() .
.
又因![]() 时,
时,![]() 为正整数,则
为正整数,则![]() ④
④
据③④![]() ,即
,即![]() 时,
时,![]() 成立.
成立.
由1![]() ,2
,2![]() 知,对任意
知,对任意![]() ,
,![]() .
.
江西文21
设![]() 为等比数列,
为等比数列,![]() ,
,![]() .
.
(1)求最小的自然数![]() ,使
,使![]() ;
;
(2)求和:![]() .
.
解:(1)由已知条件得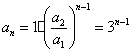 ,
,
因为![]() ,所以,使
,所以,使![]() 成立的最小自然数
成立的最小自然数![]() .
.
(2)因为![]() ,…………①
,…………①
![]() ,…………②
,…………②
![]() 得:
得:![]()
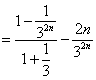
![]()
所以![]() .
.
江苏理20
已知 ![]() 是等差数列,
是等差数列,![]() 是公比为
是公比为![]() 的等比数列,
的等比数列,![]() ,记
,记![]() 为数列
为数列![]() 的前
的前![]() 项和,
项和,
(1)若![]() 是大于
是大于![]() 的正整数
的正整数![]() ,求证:
,求证:![]() ;(4分)
;(4分)
(2)若![]() 是某一正整数
是某一正整数![]() ,求证:
,求证:![]() 是整数,且数列
是整数,且数列![]() 中每一项都是数列
中每一项都是数列![]() 中的项;(8分)
中的项;(8分)
(3)是否存在这样的正数![]() ,使等比数列
,使等比数列![]() 中有三项成等差数列?若存在,写出一个
中有三项成等差数列?若存在,写出一个![]() 的值,并加以说明;若不存在,请说明理由;(4分)
的值,并加以说明;若不存在,请说明理由;(4分)
解:设![]() 的公差为
的公差为![]() ,由
,由![]() ,知
,知![]() ,
,![]() (
(![]() )
)
(1)因为![]() ,所以
,所以![]() ,
,
![]() ,
,
所以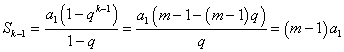
(2)![]() ,由
,由![]() ,
,
所以![]() 解得,
解得,![]() 或
或![]() ,但
,但![]() ,所以
,所以![]() ,因为
,因为![]() 是正整数,所以
是正整数,所以![]() 是整数,即
是整数,即![]() 是整数,设数列
是整数,设数列![]() 中任意一项为
中任意一项为
![]() ,设数列
,设数列![]() 中的某一项
中的某一项![]()
![]() =
=![]()
现在只要证明存在正整数![]() ,使得
,使得![]() ,即在方程
,即在方程![]() 中
中![]() 有正整数解即可,
有正整数解即可,![]() ,所以
,所以
![]() ,若
,若![]() ,则
,则![]() ,那么
,那么![]() ,当
,当![]() 时,因为
时,因为![]() ,只要考虑
,只要考虑![]() 的情况,因为
的情况,因为![]() ,所以
,所以![]() ,因此
,因此![]() 是正整数,所以
是正整数,所以![]() 是正整数,因此数列
是正整数,因此数列![]() 中任意一项为
中任意一项为
![]() 与数列
与数列![]() 的第
的第![]() 项相等,从而结论成立。
项相等,从而结论成立。
(3)设数列![]() 中有三项
中有三项![]() 成等差数列,则有
成等差数列,则有
2![]() 设
设![]() ,所以2
,所以2![]() ,令
,令![]() ,则
,则![]()
![]() ,因为
,因为![]() ,所以
,所以![]() ,所以
,所以![]() ,即存在
,即存在![]() 使得
使得![]() 中有三项
中有三项![]() 成等差数列。
成等差数列。
湖南理21
已知![]() (
(![]() )是曲线
)是曲线![]() 上的点,
上的点,![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,且满足
项和,且满足![]() ,
,![]() ,
,![]() ….
….
(I)证明:数列![]() (
(![]() )是常数数列;
)是常数数列;
(II)确定![]() 的取值集合
的取值集合![]() ,使
,使![]() 时,数列
时,数列![]() 是单调递增数列;
是单调递增数列;
(III)证明:当![]() 时,弦
时,弦![]() (
(![]() )的斜率随
)的斜率随![]() 单调递增
单调递增
解:(I)当![]() 时,由已知得
时,由已知得![]() .
.
因为![]() ,所以
,所以![]() .
…… ①
.
…… ①
于是![]() .
……②
.
……②
由②-①得![]() .
…… ③
.
…… ③
于是![]() . …… ④
. …… ④
由④-③得![]() ,
…… ⑤
,
…… ⑤
所以![]() ,即数列
,即数列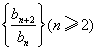 是常数数列.
是常数数列.
(II)由①有![]() ,所以
,所以![]() .由③有
.由③有![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
而 ⑤表明:数列![]() 和
和![]() 分别是以
分别是以![]() ,
,![]() 为首项,6为公差的等差数列,
为首项,6为公差的等差数列,
所以![]() ,
,![]() ,
,![]() ,
,
数列![]() 是单调递增数列
是单调递增数列![]() 且
且![]() 对任意的
对任意的![]() 成立.
成立.
![]() 且
且![]()
![]()
![]() .
.
即所求![]() 的取值集合是
的取值集合是![]() .
.
(III)解法一:弦![]() 的斜率为
的斜率为![]()
任取![]() ,设函数
,设函数![]() ,则
,则![]()
记![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数,
上为增函数,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为减函数,
上为减函数,
所以![]() 时,
时,![]() ,从而
,从而![]() ,所以
,所以![]() 在
在![]() 和
和![]() 上都是增函数.
上都是增函数.
由(II)知,![]() 时,数列
时,数列![]() 单调递增,
单调递增,
取![]() ,因为
,因为![]() ,所以
,所以![]()
![]() .
.
取![]() ,因为
,因为![]() ,所以
,所以![]()
![]() .
.
所以![]() ,即弦
,即弦![]() 的斜率随
的斜率随![]() 单调递增.
单调递增.
解法二:设函数![]() ,同解法一得,
,同解法一得,![]() 在
在![]() 和
和![]() 上都是增函数,
上都是增函数,
所以![]() ,
,![]() .
.
故![]() ,即弦
,即弦![]() 的斜率随
的斜率随![]() 单调递增.
单调递增.
湖南文20
设![]() 是数列
是数列![]() (
(![]() )的前
)的前![]() 项和,
项和,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
(I)证明:数列![]() (
(![]() )是常数数列;
)是常数数列;
(II)试找出一个奇数![]() ,使以18为首项,7为公比的等比数列
,使以18为首项,7为公比的等比数列![]() (
(![]() )中的所有项都是数列
)中的所有项都是数列![]() 中的项,并指出
中的项,并指出![]() 是数列
是数列![]() 中的第几项.
中的第几项.
20.解:(I)当![]() 时,由已知得
时,由已知得![]() .
.
因为![]() ,所以
,所以![]() . …………………………①
. …………………………①
于是![]() . …………………………………………………②
. …………………………………………………②
由②-①得:![]() .……………………………………………③
.……………………………………………③
于是![]() .……………………………………………………④
.……………………………………………………④
由④-③得:![]() .…………………………………………………⑤
.…………………………………………………⑤
即数列![]() (
(![]() )是常数数列.
)是常数数列.
(II)由①有![]() ,所以
,所以![]() .
.
由③有![]() ,所以
,所以![]() ,
,
而⑤表明:数列![]() 和
和![]() 分别是以
分别是以![]() ,
,![]() 为首项,6为公差的等差数列.
为首项,6为公差的等差数列.
所以![]() ,
,![]() ,
,![]() .
.
由题设知,![]() .当
.当![]() 为奇数时,
为奇数时,![]() 为奇数,而
为奇数,而![]() 为偶数,所以
为偶数,所以![]() 不是数列
不是数列![]() 中的项,
中的项,![]() 只可能是数列
只可能是数列![]() 中的项.
中的项.
若![]() 是数列
是数列![]() 中的第
中的第![]() 项,由
项,由![]() 得
得![]() ,取
,取![]() ,得
,得![]() ,此时
,此时![]() ,由
,由![]() ,得
,得![]() ,
,![]()
![]() ,从而
,从而![]() 是数列
是数列![]() 中的第
中的第![]() 项.
项.
(注:考生取满足![]() ,
,![]() 的任一奇数,说明
的任一奇数,说明![]() 是数列
是数列![]() 中的第
中的第![]() 项即可)
项即可)
湖北理21
已知![]() 为正整数,
为正整数,
(I)用数学归纳法证明:当![]() 时,
时,![]() ;
;
(II)对于![]() ,已知
,已知![]() ,求证
,求证![]() ,
,
求证![]() ,
,![]() ;
;
(III)求出满足等式![]() 的所有正整数
的所有正整数![]() .
.
本小题主要考查数学归纳法、数列求和、不等式等基础知识和基本的运算技能,考查分析问题能力和推理能力.
解法1:(Ⅰ)证:用数学归纳法证明:
(ⅰ)当![]() 时,原不等式成立;当
时,原不等式成立;当![]() 时,左边
时,左边![]() ,右边
,右边![]() ,
,
因为![]() ,所以左边
,所以左边![]() 右边,原不等式成立;
右边,原不等式成立;
(ⅱ)假设当![]() 时,不等式成立,即
时,不等式成立,即![]() ,则当
,则当![]() 时,
时,
![]() ,
,![]() ,于是在不等式
,于是在不等式![]() 两边同乘以
两边同乘以![]() 得
得
![]() ,
,
所以![]() .即当
.即当![]() 时,不等式也成立.
时,不等式也成立.
综合(ⅰ)(ⅱ)知,对一切正整数![]() ,不等式都成立.
,不等式都成立.
(Ⅱ)证:当![]() 时,由(Ⅰ)得
时,由(Ⅰ)得![]() ,
,
于是![]()
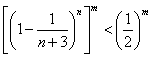 ,
,![]() .
.
(Ⅲ)解:由(Ⅱ)知,当![]() 时,
时,
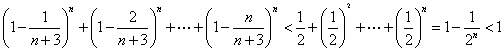 ,
,
![]() .
.
即![]() .即当
.即当![]() 时,不存在满足该等式的正整数
时,不存在满足该等式的正整数![]() .
.
故只需要讨论![]() 的情形:
的情形:
当![]() 时,
时,![]() ,等式不成立;
,等式不成立;
当![]() 时,
时,![]() ,等式成立;
,等式成立;
当![]() 时,
时,![]() ,等式成立;
,等式成立;
当![]() 时,
时,![]() 为偶数,而
为偶数,而![]() 为奇数,故
为奇数,故![]() ,等式不成立;
,等式不成立;
当![]() 时,同
时,同![]() 的情形可分析出,等式不成立.
的情形可分析出,等式不成立.
综上,所求的![]() 只有
只有![]() .
.
解法2:(Ⅰ)证:当![]() 或
或![]() 时,原不等式中等号显然成立,下用数学归纳法证明:
时,原不等式中等号显然成立,下用数学归纳法证明:
当![]() ,且
,且![]() 时,
时,![]() ,
,![]() . ①
. ①
(ⅰ)当![]() 时,左边
时,左边![]() ,右边
,右边![]() ,因为
,因为![]() ,所以
,所以![]() ,即左边
,即左边![]() 右边,不等式①成立;
右边,不等式①成立;
(ⅱ)假设当![]() 时,不等式①成立,即
时,不等式①成立,即![]() ,则当
,则当![]() 时,
时,
因为![]() ,所以
,所以![]() .又因为
.又因为![]() ,所以
,所以![]() .
.
于是在不等式![]() 两边同乘以
两边同乘以![]() 得
得
![]() ,
,
所以![]() .即当
.即当![]() 时,不等式①也成立.
时,不等式①也成立.
综上所述,所证不等式成立.
(Ⅱ)证:当![]() ,
,![]() 时,
时,![]() ,
,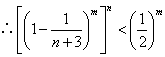 ,
,
而由(Ⅰ),![]() ,
,
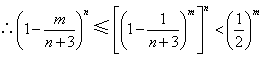 .
.
(Ⅲ)解:假设存在正整数![]() 使等式
使等式![]() 成立,
成立,
即有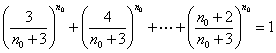 . ②
. ②
又由(Ⅱ)可得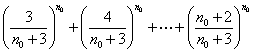
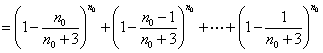
![]() ,与②式矛盾.
,与②式矛盾.
故当![]() 时,不存在满足该等式的正整数
时,不存在满足该等式的正整数![]() .
.
下同解法1.
湖北文20
已知数列![]() 和
和![]() 满足:
满足:![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ),且
),且![]() 是以
是以![]() 为公比的等比数列.
为公比的等比数列.
(I)证明:![]() ;
;
(II)若![]() ,证明数列
,证明数列![]() 是等比数列;
是等比数列;
(III)求和:![]() .
.
本小题主要考查等比数列的定义,通项公式和求和公式等基本知识及基本的运算技能,考查分析问题能力和推理能力.
解法1:(I)证:由![]() ,有
,有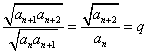 ,
,![]()
![]() .
.
(II)证:![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
![]() 是首项为5,以
是首项为5,以![]() 为公比的等比数列.
为公比的等比数列.
(III)由(II)得![]() ,
,![]() ,于是
,于是
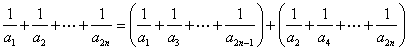
![]()
![]() .
.
当![]() 时,
时,![]()
![]() .
.
当![]() 时,
时,![]()
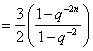
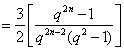 .
.
故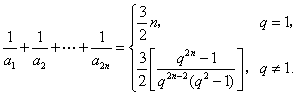
解法2:(I)同解法1(I).
(II)证:
![]() ,又
,又![]() ,
,
![]() 是首项为5,以
是首项为5,以![]() 为公比的等比数列.
为公比的等比数列.
(III)由(II)的类似方法得![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
![]() .
.
下同解法1.
广东理21
已知函数![]() ,
,![]() 是方程f(x)=0的两个根
是方程f(x)=0的两个根![]() ,
,![]() 是f(x)的导数;设
是f(x)的导数;设![]() ,
,![]() (n=1,2,……)
(n=1,2,……)
(1)求![]() 的值;
的值;
(2)证明:对任意的正整数n,都有![]() >a;
>a;
(3)记![]() (n=1,2,……),求数列{bn}的前n项和Sn。
(n=1,2,……),求数列{bn}的前n项和Sn。
解析:(1)∵![]() ,
,![]() 是方程f(x)=0的两个根
是方程f(x)=0的两个根![]() ,
,
∴![]() ;
;
(2)![]() ,
,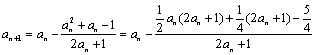
=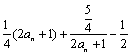 ,∵
,∵![]() ,∴有基本不等式可知
,∴有基本不等式可知![]() (当且仅当
(当且仅当![]() 时取等号),∴
时取等号),∴![]() 同,样
同,样![]() ,……,
,……,![]() (n=1,2,……),
(n=1,2,……),
(3)![]() ,而
,而![]() ,即
,即![]() ,
,
![]() ,同理
,同理![]() ,
,![]() ,又
,又![]()
![]()
广东文20
已知函数![]() ,
,![]() 、
、![]() 是方程
是方程![]() 的两个根(
的两个根(![]() ),
),![]() 是的导数
是的导数
设![]() ,
,![]() ,
,![]() .
.
(1)求![]() 、
、![]() 的值;
的值;
(2)已知对任意的正整数![]() 有
有![]() ,记
,记![]() ,
,![]() .求数列{
.求数列{![]() }的
}的
前![]() 项和
项和![]() .
.
(1) 由 ![]() 得
得![]()
![]()
![]()
(2) ![]()
![]()
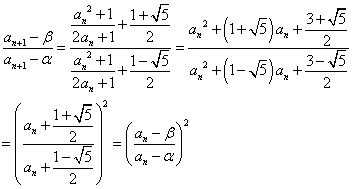
![]()
![]() 又
又 ![]()
![]() 数列
数列![]() 是一个首项为
是一个首项为
![]() ,公比为2的等比数列;
,公比为2的等比数列;
![]()
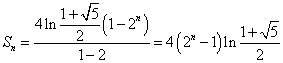
福建理21
等差数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(Ⅰ)求数列![]() 的通项
的通项![]() 与前
与前![]() 项和
项和![]() ;
;
(Ⅱ)设![]() ,求证:数列
,求证:数列![]() 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.
本小题考查数列的基本知识,考查等差数列的概念、通项公式与前![]() 项和公式,考查等比数列的概念与性质,考查化归的数学思想方法以及推理和运算能力.满分12分
项和公式,考查等比数列的概念与性质,考查化归的数学思想方法以及推理和运算能力.满分12分
解:(Ⅰ)由已知得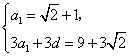 ,
,![]() ,
,
故![]() .
.
(Ⅱ)由(Ⅰ)得![]() .
.
假设数列![]() 中存在三项
中存在三项![]() (
(![]() 互不相等)成等比数列,则
互不相等)成等比数列,则![]() .
.
即![]() .
.
![]()
![]() ,
,
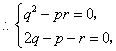
![]() .
.
与![]() 矛盾.
矛盾.
所以数列![]() 中任意不同的三项都不可能成等比数列.
中任意不同的三项都不可能成等比数列.
福建文21
数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求数列![]() 的通项
的通项![]() ;
;
(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() .
.
本小题考查数列的基本知识,考查等比数列的概念、通项公式及数列的求和,考查分类讨论及化归的数学思想方法,以及推理和运算能力.满分12分.
解:(Ⅰ)![]() ,
,
![]() ,
,
![]() .
.
又![]() ,
,
![]() 数列
数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,![]() .
.
当![]() 时,
时,![]() ,
,
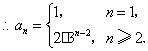
(Ⅱ)![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,…………①
,…………①
![]() ,………………………②
,………………………②
![]() 得:
得:![]()
![]()
![]() .
.
![]() .
.
又![]() 也满足上式,
也满足上式,
![]() .
.
北京理15,文科16
数列![]() 中,
中,![]() ,
,![]() (
(![]() 是常数,
是常数,![]() ),且
),且![]() 成公比不为
成公比不为![]() 的等比数列.
的等比数列.
(I)求![]() 的值;
的值;
(II)求![]() 的通项公式.
的通项公式.
解:(I)![]() ,
,![]() ,
,![]() ,
,
因为![]() ,
,![]() ,
,![]() 成等比数列,
成等比数列,
所以![]() ,
,
解得![]() 或
或![]() .
.
当![]() 时,
时,![]() ,不符合题意舍去,故
,不符合题意舍去,故![]() .
.
(II)当![]() 时,由于
时,由于
![]() ,
,
![]() ,
,
![]()
![]() ,
,
所以![]() .
.
又![]() ,
,![]() ,故
,故![]() .
.
当![]() 时,上式也成立,
时,上式也成立,
所以![]() .
.
安徽理21
某国采用养老储备金制度.公民在就业的第一年就交纳养老储备金,数目为a1,以后每年交纳的数目均比上一年增加d(d>0),因此,历年所交纳的储务金数目a1,a2,…是一个公差为d的等差数列,与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.这就是说,如果固定年利率为r(r>0),那么,在第n年末,第一年所交纳的储备金就变为a1(1+r)n-1,第二年所交纳的储备金就变为a2(1+r)n-2,……,以Tn表示到第n年末所累计的储备金总额.
(Ⅰ)写出Tn与Tn-1(n≥2)的递推关系式;
(Ⅱ)求证:Tn=An+Bn,其中{An}是一个等比数列,{Bn}是一个等差数列.
本小题主要考查等差数列、等比数列的基本概念和基本方法,考查学生阅读资料、提取信息、建立数学模型的能力、考查应用所学知识分析和解决实际问题的能力.本小题满分14分.
解:(Ⅰ)我们有![]() .
.
(Ⅱ)![]() ,对
,对![]() 反复使用上述关系式,得
反复使用上述关系式,得
![]()
![]() , ①
, ①
在①式两端同乘![]() ,得
,得
![]() ②
②
②![]() ①,得
①,得![]()
![]() .
.
即![]() .
.
如果记![]() ,
,![]() ,
,
则![]() .
.
其中![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列;
为公比的等比数列;![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列.
为公差的等差数列.
安徽文21
某国采用养老储备金制度,公民在就业的第一年就交纳养老储备金,数目为a1,以后第年交纳的数目均比上一年增加d(d>0),因此,历年所交纳的储备金数目a1,a2,…是一个公差为d的等差数列,与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利,这就是说,如果固定年利率为r(r>0),那么,在第n年末,第一年所交纳的储备金就变为n(1+r)n-1,第二年所交纳的储备金就变为a2(1+r)n-2,……,以Tn表示到第n年末所累计的储备金总额.
(Ⅰ)写出Tn与Tn-1(n≥2)的递推关系式;
本小题主要考查等差数列、等比数列的基本概念和基本方法,考查学生阅读资料、提取信息、建立数学模型的能力、考查应用所学知识分析和解决实际问题的能力.本小题满分14分.
解:(Ⅰ)我们有![]() .
.
(Ⅱ)![]() ,对
,对![]() 反复使用上述关系式,得
反复使用上述关系式,得
![]()
![]() , ①
, ①
在①式两端同乘![]() ,得
,得
![]() ②
②
②![]() ①,得
①,得![]()
![]() .
.
即![]() .
.
如果记![]() ,
,![]() ,
,
则![]() .
.
其中![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列;
为公比的等比数列;![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列.
为公差的等差数列.
辽宁文20
已知数列![]() ,
,![]() 满足
满足![]() ,
,![]() ,且
,且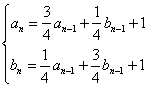 (
(![]() )
)
(I)令![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(II)求数列![]() 的通项公式及前
的通项公式及前![]() 项和公式
项和公式![]() .
.
本小题主要考查等差数列,等比数列等基础知识,考查基本运算能力.满分12分.
(I)解:由题设得![]() ,即
,即
![]() (
(![]() )
)
易知![]() 是首项为
是首项为![]() ,公差为2的等差数列,通项公式为
,公差为2的等差数列,通项公式为
![]() .
.
(II)解:由题设得![]() ,令
,令![]() ,则
,则
![]() .
.
易知![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,通项公式为
的等比数列,通项公式为
![]() .
.
由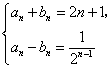 解得
解得
![]() ,
,
求和得![]()