高中毕业班数学全国统一考试试题
数学(理工类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟.第Ⅰ卷1至2页,第Ⅱ卷3至10页.考试结束后,将本试卷和答题卡一并交回.
祝各位考生考试顺利!
第Ⅰ卷
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考号、科目涂写在答题卡上,并在规定位置粘贴考试用条形码.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.答在试卷上的无效.
3.本卷共10小题,每小题5分,共50分.
参考公式:
·如果事件![]() 互斥,那么 球的表面积公式
互斥,那么 球的表面积公式
![]()
![]()
·如果事件![]() 相互独立,那么 其中
相互独立,那么 其中![]() 表示球的半径
表示球的半径
![]()
一、选择题:在每小题列出的四个选项中,只有一项是符合题目要求的.
1.![]() 是虚数单位,
是虚数单位,![]() ( )
( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
2.设变量![]() 满足约束条件
满足约束条件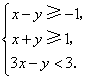 则目标函数
则目标函数![]() 的最大值为( )
的最大值为( )
A.4 B.11 C.12 D.14
3.“![]() ”是“
”是“![]() ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
4.设双曲线![]() 的离心率为
的离心率为![]() ,且它的一条准线与抛物线
,且它的一条准线与抛物线![]() 的准线重合,则此双曲线的方程为( )
的准线重合,则此双曲线的方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.函数![]() 的反函数是( )
的反函数是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.设![]() 为两条直线,
为两条直线,![]() 为两个平面,下列四个命题中,正确的命题是( )
为两个平面,下列四个命题中,正确的命题是( )
A.若![]() 与
与![]() 所成的角相等,则
所成的角相等,则![]()
B.若![]() ,
,![]() ,则
,则![]()
C.若![]() ,则
,则![]()
D.若![]() ,
,![]() ,则
,则![]()
7.在![]() 上定义的函数
上定义的函数![]() 是偶函数,且
是偶函数,且![]() ,若
,若![]() 在区间
在区间![]() 上是减函数,则
上是减函数,则![]() ( )
( )
A.在区间![]() 上是增函数,在区间
上是增函数,在区间![]() 上是增函数
上是增函数
B.在区间![]() 上是增函数,在区间
上是增函数,在区间![]() 上是减函数
上是减函数
C.在区间![]() 上是减函数,在区间
上是减函数,在区间![]() 上是增函数
上是增函数
D.在区间![]() 上是减函数,在区间
上是减函数,在区间![]() 上是减函数
上是减函数
8.设等差数列![]() 的公差
的公差![]() 不为0,
不为0,![]() .若
.若![]() 是
是![]() 与
与![]() 的等比中项,则
的等比中项,则![]() ( )
( )
A.2 B.4 C.6 D.8
9.设![]() 均为正数,且
均为正数,且![]() ,
,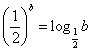 ,
,![]() .则( )
.则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.设两个向量![]() 和
和![]() ,其中
,其中![]() 为实数.若
为实数.若![]() ,中央电视台
,中央电视台![]() 的取值范围是( )
的取值范围是( )
A. B.![]() C. D.
C. D.
高中毕业班数学全国统一考试试题
数学(理工类)
第Ⅱ卷
注意事项:
1.答案前将密封线内的项目填写清楚.
2.用钢笔或圆珠笔直接答在试卷上.
3.本卷共12小题,共100分.
二、填空题:本大题共6小题,每小题4分,共24分,把答案填在题中横线上.
11.若![]() 的二项展开式中
的二项展开式中![]() 的系数为
的系数为![]() ,则
,则![]() (用数字作答).
(用数字作答).
12.一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为 .
13.设等差数列![]() 的公差
的公差![]() 是2,前
是2,前![]() 项的和为
项的和为![]() ,则
,则![]() .
.
 14.已知两圆
14.已知两圆![]() 和
和![]() 相交于
相交于![]() 两点,则直线
两点,则直线![]() 的方程是 .
的方程是 .
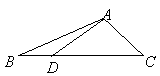
15.如图,在![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上一点,
上一点,![]() ,则
,则![]() .
.
![]() 16.如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求最多使用3种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有 种(用数字作答).
16.如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求最多使用3种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有 种(用数字作答).
三、解答题:本大题共6小题,共76分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
已知函数![]() .
.
(Ⅰ)求函数![]() 的最小正周期;
的最小正周期;
(Ⅱ)求函数![]() 在区间
在区间![]() 上的最小值和最大值.
上的最小值和最大值.
18.(本小题满分12分)
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
(Ⅲ)设![]() 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
19.(本小题满分12分)
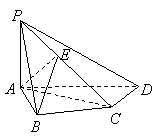
如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
 (Ⅰ)证明
(Ⅰ)证明![]() ;
;
(Ⅱ)证明![]() 平面
平面![]() ;
;
(Ⅲ)求二面角![]() 的大小.
的大小.
20.(本小题满分12分)
已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)当![]() 时,求函数
时,求函数![]() 的单调区间与极值.
的单调区间与极值.
21.(本小题满分14分)
在数列![]() 中,
中,![]() ,其中
,其中![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)证明存在![]() ,使得
,使得![]() 对任意
对任意![]() 均成立.
均成立.
22.(本小题满分14分)
设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 是椭圆上的一点,
是椭圆上的一点,![]() ,原点
,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)证明![]() ;
;
(Ⅱ)设![]() 为椭圆上的两个动点,
为椭圆上的两个动点,![]() ,过原点
,过原点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
数学(理工类)参考解答
一、选择题:本题考查基本知识和基本运算.每小题5分,满分50分.
1.C 2.B 3.A 4.D 5.C
6.D 7.B 8.B 9.A 10.A
二、填空题:本题考查基本知识和基本运算.每小题4分,满分24分.
11.2 12.![]() 13.3
13.3
14.![]() 15.
15.![]() 16.390
16.390
三、解答题
17.本小题考查三角函数中的诱导公式、特殊角三角函数值、两角差公式、倍角公式、函数![]() 的性质等基础知识,考查基本运算能力.满分12分.
的性质等基础知识,考查基本运算能力.满分12分.
(Ⅰ)解:![]() .
.
因此,函数![]() 的最小正周期为
的最小正周期为![]() .
.
(Ⅱ)解法一:因为![]() 在区间
在区间![]() 上为增函数,在区间
上为增函数,在区间![]() 上为减函数,又
上为减函数,又![]() ,
,![]() ,
,![]() ,
,
故函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() .
.
解法二:作函数![]() 在长度为一个周期的区间
在长度为一个周期的区间![]() 上的图象如下:
上的图象如下:
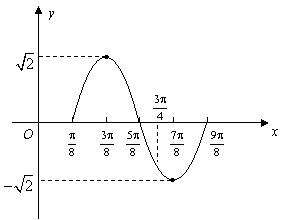
由图象得函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() .
.
18.本小题主要考查互斥事件、相互独立事件、离散型随机变量的分布列和数学期望等基础知识,考查运用概率知识解决实际问题的能力.满分12分.
(Ⅰ)解:设“从甲盒内取出的2个球均为黑球”为事件![]() ,“从乙盒内取出的2个球均为黑球”为事件
,“从乙盒内取出的2个球均为黑球”为事件![]() .由于事件
.由于事件![]() 相互独立,且
相互独立,且![]() ,
,![]() .
.
故取出的4个球均为黑球的概率为![]() .
.
(Ⅱ)解:设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件![]() ,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件
,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件![]() .由于事件
.由于事件![]() 互斥,
互斥,
且![]() ,
,![]() .
.
故取出的4个球中恰有1个红球的概率为![]() .
.
(Ⅲ)解:![]() 可能的取值为
可能的取值为![]() .由(Ⅰ),(Ⅱ)得
.由(Ⅰ),(Ⅱ)得![]() ,
,![]() ,
,
![]() .从而
.从而![]() .
.
![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 | 3 |
|
|
|
|
|
|
![]() 的数学期望
的数学期望![]() .
.
19.本小题考查直线与直线垂直、直线与平面垂直、二面角等基础知识,考查空间想象能力、运算能力和推理论证能力.满分12分.
(Ⅰ)证明:在四棱锥![]() 中,因
中,因![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,故
,故![]() .
.
![]() ,
,![]() 平面
平面![]() .
.
而![]() 平面
平面![]() ,
,![]() .
.
(Ⅱ)证明:由![]() ,
,![]() ,可得
,可得![]() .
.
![]() 是
是![]() 的中点,
的中点,![]() .
.
由(Ⅰ)知,![]() ,且
,且![]() ,所以
,所以![]() 平面
平面![]() .
.
而![]() 平面
平面![]() ,
,![]() .
.
![]() 底面
底面![]() 在底面
在底面![]() 内的射影是
内的射影是![]() ,
,![]() ,
,![]() .
.
又![]() ,综上得
,综上得![]() 平面
平面![]() .
.
(Ⅲ)解法一:过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .则(Ⅱ)知,
.则(Ⅱ)知,![]() 平面
平面![]() ,
,![]() 在平面
在平面![]() 内的射影是
内的射影是![]() ,则
,则![]() .
.
因此![]() 是二面角
是二面角![]() 的平面角.
的平面角.
由已知,得![]() .设
.设![]() ,
,
可得![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
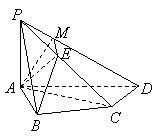 则
则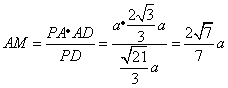 .
.
在![]() 中,
中,![]() .
.
所以二面角![]() 的大小是
的大小是![]() .
.
解法二:由题设![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,则平面
,则平面![]() 平面
平面![]() ,交线为
,交线为![]() .
.
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,故
,故![]() 平面
平面![]() .过点
.过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,故
,故![]() .因此
.因此![]() 是二面角
是二面角![]() 的平面角.
的平面角.
由已知,可得![]() ,设
,设![]() ,
,
可得![]() .
.
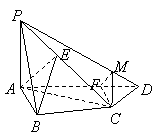
![]() ,
,![]() .
.
于是,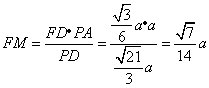 .
.
在![]() 中,
中,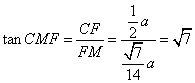 .
.
所以二面角![]() 的大小是
的大小是![]() .
.
20.本小题考查导数的几何意义,两个函数的和、差、积、商的导数,利用导数研究函数的单调性和极值等基础知识,考查运算能力及分类讨论的思想方法.满分12分.
(Ⅰ)解:当![]() 时,
时,![]() ,
,![]() ,
,
又![]() ,
,![]() .
.
所以,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() .
.
(Ⅱ)解:![]() .
.
由于![]() ,以下分两种情况讨论.
,以下分两种情况讨论.
(1)当![]() 时,令
时,令![]() ,得到
,得到![]() ,
,![]() .当
.当![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
| 0 |
| 0 |
|
|
|
| 极小值 |
| 极大值 |
|
所以![]() 在区间
在区间![]() ,
,![]() 内为减函数,在区间
内为减函数,在区间![]() 内为增函数.
内为增函数.
函数![]() 在
在![]() 处取得极小值
处取得极小值![]() ,且
,且![]() ,
,
函数![]() 在
在![]() 处取得极大值
处取得极大值![]() ,且
,且![]() .
.
(2)当![]() 时,令
时,令![]() ,得到
,得到![]() ,当
,当![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
| 0 |
| 0 |
|
|
|
| 极大值 |
| 极小值 |
|
所以![]() 在区间
在区间![]() ,
,![]() 内为增函数,在区间
内为增函数,在区间![]() 内为减函数.
内为减函数.
函数![]() 在
在![]() 处取得极大值
处取得极大值![]() ,且
,且![]() .
.
函数![]() 在
在![]() 处取得极小值
处取得极小值![]() ,且
,且![]() .
.
21.本小题以数列的递推关系式为载体,主要考查等比数列的前![]() 项和公式、数列求和、不等式的证明等基础知识与基本方法,考查归纳、推理、运算及灵活运用数学知识分析问题和解决问题的能力.满分14分.
项和公式、数列求和、不等式的证明等基础知识与基本方法,考查归纳、推理、运算及灵活运用数学知识分析问题和解决问题的能力.满分14分.
(Ⅰ)解法一:![]() ,
,
![]() ,
,
![]() .
.
由此可猜想出数列![]() 的通项公式为
的通项公式为![]() .
.
以下用数学归纳法证明.
(1)当![]() 时,
时,![]() ,等式成立.
,等式成立.
(2)假设当![]() 时等式成立,即
时等式成立,即![]() ,
,
那么![]()
![]()
![]() .
.
这就是说,当![]() 时等式也成立.根据(1)和(2)可知,等式
时等式也成立.根据(1)和(2)可知,等式![]() 对任何
对任何![]() 都成立.
都成立.
解法二:由![]() ,
,![]() ,
,
可得![]() ,
,
所以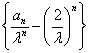 为等差数列,其公差为1,首项为0,故
为等差数列,其公差为1,首项为0,故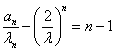 ,所以数列
,所以数列![]() 的通项公式为
的通项公式为![]() .
.
(Ⅱ)解:设![]() , ①
, ①
![]() ②
②
当![]() 时,①式减去②式,
时,①式减去②式,
得![]() ,
,
![]() .
.
这时数列![]() 的前
的前![]() 项和
项和![]() .
.
当![]() 时,
时,![]() .这时数列
.这时数列![]() 的前
的前![]() 项和
项和![]() .
.
(Ⅲ)证明:通过分析,推测数列![]() 的第一项
的第一项![]() 最大,下面证明:
最大,下面证明:
![]() . ③
. ③
由![]() 知
知![]() ,要使③式成立,只要
,要使③式成立,只要![]() ,
,
因为![]()
![]()
![]() .
.
所以③式成立.
因此,存在![]() ,使得
,使得![]() 对任意
对任意![]() 均成立.
均成立.
22.本小题主要考查椭圆的标准方程和几何性质、直线方程、求曲线的方程等基础知识,考查曲线和方程的关系等解析几何的基本思想方法及推理、运算能力.满分14分.
(Ⅰ)证法一:由题设![]() 及
及![]() ,
,![]() ,不妨设点
,不妨设点![]() ,其中
,其中![]() .由于点
.由于点![]() 在椭圆上,有
在椭圆上,有![]() ,即
,即![]() .
.
解得![]() ,从而得到
,从而得到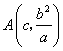 .
.
直线![]() 的方程为
的方程为![]() ,整理得
,整理得![]() .
.
由题设,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,即
,即![]() ,
,
将![]() 代入上式并化简得
代入上式并化简得![]() ,即
,即![]() .
.
证法二:同证法一,得到点![]() 的坐标为
的坐标为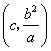 .
.
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,易知
,易知![]()
![]()
![]() ,故
,故![]() .
.
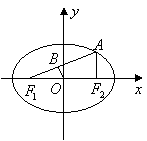 由椭圆定义得
由椭圆定义得![]() ,又
,又![]() ,
,
所以![]() ,
,
解得![]() ,而
,而![]() ,得
,得![]() ,即
,即![]() .
.
(Ⅱ)解法一:设点![]() 的坐标为
的坐标为![]() .
.
当![]() 时,由
时,由![]() 知,直线
知,直线![]() 的斜率为
的斜率为![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,或
,或![]() ,其中
,其中![]() ,
,![]() .
.
点![]() 的坐标满足方程组
的坐标满足方程组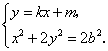
将①式代入②式,得![]() ,
,
整理得![]() ,
,
于是![]() ,
,![]() .
.
由①式得![]()
![]() .
.
由![]() 知
知![]() .将③式和④式代入得
.将③式和④式代入得![]() ,
,
![]() .
.
将![]() 代入上式,整理得
代入上式,整理得![]() .
.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,
,![]() 的坐标满足方程组
的坐标满足方程组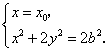
所以![]() ,
,![]() .
.
由![]() 知
知![]() ,即
,即![]() ,
,
解得![]() .
.
这时,点![]() 的坐标仍满足
的坐标仍满足![]() .
.
综上,点![]() 的轨迹方程为
的轨迹方程为 ![]() .
.
解法二:设点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,由
,由![]() ,垂足为
,垂足为![]() ,可知直线
,可知直线![]() 的方程为
的方程为![]() .
.
记![]() (显然
(显然![]() ),点
),点![]() 的坐标满足方程组
的坐标满足方程组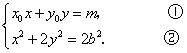
由①式得![]() . ③
. ③
由②式得![]() . ④
. ④
将③式代入④式得![]() .
.
整理得![]() ,
,
于是![]() . ⑤
. ⑤
由①式得![]() . ⑥
. ⑥
由②式得![]() . ⑦
. ⑦
将⑥式代入⑦式得![]() ,
,
整理得![]() ,
,
于是![]() . ⑧
. ⑧
由![]() 知
知![]() .将⑤式和⑧式代入得
.将⑤式和⑧式代入得![]() ,
,
![]() .
.
将![]() 代入上式,得
代入上式,得![]() .
.
所以,点![]() 的轨迹方程为
的轨迹方程为![]() .
.