高中毕业班数学质量检查试题
数学(理工农医类)试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),共4页。
全卷满分150分,考试时间120分钟。
注意事项:
1.考生将自己的姓名、准考证号及所有答案均填写在答题卡上。
2.答题要求,见答题卡上的“填涂样例”和“注意事项”。
参考公式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B)
![]()
如果事件A、B相互独立,那么 其中R表示球的半径
P(A·B)=P(A)·P(B) 球的体积公式
如果事件A在一次试验中发生的概率是P,那么
![]()
![]() 次独立重复试验中恰好发生
次独立重复试验中恰好发生![]() 次的概率
其中R表示球的半径
次的概率
其中R表示球的半径
![]()
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个答案中,只有一项是符合题目要求的。
1.设集合![]() ,
,![]() ,则
,则![]() 为
为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.复数![]() ,
,![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.一个田径队,有男运动员30人,女运动员20人,比赛后,立即用分层抽样的方法,从全体队员中抽出一个容量为10的样本进行尿样兴奋剂检查,其中男运动员应抽
A.3人 B.4人 C.5人 D.6人
4.要得到函数![]() 的图象,需将函数
的图象,需将函数![]() 的图象
的图象
A.向左平移![]() 个单位
B.向右平移
个单位
B.向右平移![]() 个单位
个单位
C.向左平移![]() 个单位
D.向右平移
个单位
D.向右平移![]() 个单位
个单位
5.若随机变量![]() 的分布列是:
的分布列是:
|
| 1 | 3 | 5 |
|
| 0.2 | 0.6 |
|
则其数学期望![]() 等于
等于
A.1 B.![]() C.
C.![]() D.3
D.3
6.已知![]() 的一条渐近线方程为
的一条渐近线方程为![]() ,则双曲线的离心率为
,则双曲线的离心率为
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
7.已知函数![]() ,且
,且![]() 的解集为
的解集为![]() ,则函数
,则函数![]() 的图象大致是
的图象大致是
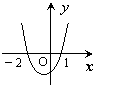 | 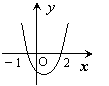 | 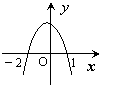 | 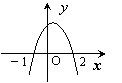 | ||||
A B C D
8.设![]() 、
、![]() 为不同的直线,
为不同的直线,![]() 为平面,且
为平面,且![]() ,下列为假命题的是
,下列为假命题的是
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]()
C.若![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]()
9.甲、乙、丙三位学生用计算机联网学习数学,每天上课后独立完成6道自我检测题,甲及格的概率为![]() ,乙及格的概率为
,乙及格的概率为![]() ,丙及格的概率为
,丙及格的概率为![]() ,三人各自检测一次,则三人中至少一人及格的概率为
,三人各自检测一次,则三人中至少一人及格的概率为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.若把英语单词“hello”的字母顺序写错了,则可能出现的错误的种数是
A.59 B.60 C.119 D.120
11.已知![]() 是定义在R上的不恒为零的函数,且对于任意的
是定义在R上的不恒为零的函数,且对于任意的![]() ,
,![]() ,
,![]() 满足关系式:
满足关系式:![]() ,则
,则![]() 的奇偶性为
的奇偶性为
A.奇函数 B.偶函数 C.非奇非偶函数 D.既是奇函数也是偶函数
12.已知![]() 、
、![]() 是椭圆
是椭圆![]() 的两个焦点,P是椭圆上的一点,若
的两个焦点,P是椭圆上的一点,若![]() 的内切圆半径为1,则点P到
的内切圆半径为1,则点P到![]() 轴的距离为
轴的距离为
A.![]() B.
B.![]() C.3
D.
C.3
D.![]()
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡对应题号的横线上。
13.在![]() 的展开式中,常数项是
(用数字作答)。
的展开式中,常数项是
(用数字作答)。
14.函数![]() ,
,![]() 的反函数是
。
的反函数是
。
15.球面上三点A、B、C,AB=AC=BC=3,若球心到截面ABC的距离等于球半径的一半,则球的表面积为 。
16.定义运算![]() *
*![]() 为:
为:![]() *
*![]() ,例如:1*2=1,则函数
,例如:1*2=1,则函数![]() *
*![]() 的值域为
。
的值域为
。
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)
已知向量![]() ,
,![]() 。
。
记函数![]() ,若函数
,若函数![]() 的最小正周期为
的最小正周期为![]() 。
。
(1)求![]() ;
;
(2)求函数![]() 的最大值,并求此时
的最大值,并求此时![]() 的值。
的值。
18.(本小题满分12分)
已知函数![]() 的图象与直线
的图象与直线![]() 相切于点
相切于点![]() 。
。
(1)求![]() 的值;
的值;
 (2)求函数
(2)求函数![]() 的单调区间和极小值。
的单调区间和极小值。
19.(本小题满分12分)
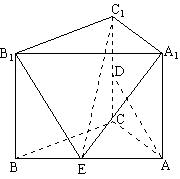
如图,在直三棱柱ABC—A1B1C1中, AA1=4,AB=5,BC=3,AC=4,D为CC1的中点。
(1)求异面直线AD与A1B1所成角的余弦值;
(2)试在线段AB上找一点E,使得:A1E⊥AD;
(3)求点D到平面B1C1E的距离。
20.(本小题满分12分)
某高速公路指挥部接到通知,24小时后将有一场超历史记录的大暴雨,为确保万无一失,指挥部决定在24小时内筑一道临时堤坝,以防山洪淹没正在紧张施工的隧道工程。经测算,除现有施工人员外,还须调用翻斗车搬运![]() 立方米的土方。已知每辆翻斗车每小时可搬运的土方量为
立方米的土方。已知每辆翻斗车每小时可搬运的土方量为![]() ,指挥部可调用25辆上述型号的翻斗车,但其中只有一辆可以立即投入施工,其余车辆需要从各处紧急抽调,每隔20分钟有一辆车到达并投入施工。
,指挥部可调用25辆上述型号的翻斗车,但其中只有一辆可以立即投入施工,其余车辆需要从各处紧急抽调,每隔20分钟有一辆车到达并投入施工。
(1)从第一辆车投入施工算起,第25辆车须多久才能到达?
(2)24小时内能否完成防洪堤坝工程?请说明理由。
21.(本小题满分12分)
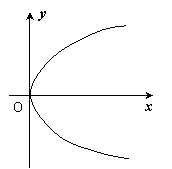 已知抛物线的顶点在原点,焦点F在
已知抛物线的顶点在原点,焦点F在![]() 轴上。M为抛物线上的点,M的横坐标为2,且MF=3。
轴上。M为抛物线上的点,M的横坐标为2,且MF=3。
(1)求此抛物线的方程;
(2)如图,过![]() 轴正半轴上任一点
轴正半轴上任一点![]() 作直线与此抛物线交于A、B两点,点Q是点P关于原点的对称点。点P分有向线段
作直线与此抛物线交于A、B两点,点Q是点P关于原点的对称点。点P分有向线段![]() 所成的比为
所成的比为![]() 。
。
求证:![]() 。
。
22.(本小题满分14分)
已知函数![]() ,若
,若![]() 的定义域为[-1,0],值域也为
的定义域为[-1,0],值域也为
[-1,0]。
(1)求出符合条件的函数![]() 的表达式;
的表达式;
(2)若数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列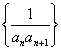 的前
的前![]() 项和为
项和为![]() ,试求
,试求![]() ;
;
(3)若数列![]() 满足
满足![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() ,问是否存在正常数A,使得对于任意正整数
,问是否存在正常数A,使得对于任意正整数![]() 都有
都有![]() ?并证明你的结论。
?并证明你的结论。
参考解答及评分标准
一、选择题:本大题共12小题,每小题5分,共60分
1.A 2.D 3.D 4.B 5.D 6.C 7.C 8.B 9.B 10.A 11.A 12.B
二、填空题:本大题共4小题,每小题4分,共16分
13.495 14.![]() 15.16
15.16![]() 16.
16.![]()
三、解答题:本大题共6小题,共74分。
17.解:∵![]() ,
,![]()
∴![]() ………………………2分
………………………2分
![]() ………………………4分
………………………4分
![]()
![]() ………………………6分
………………………6分
(1)∵函数![]() 的最小正周期
的最小正周期![]() ,
,
∴![]() ,∴
,∴![]() ………………………8分
………………………8分
(2)当![]() 时,函数
时,函数![]() 取得最大值
取得最大值![]() ,
,
此时,![]() ,解得
,解得![]() ……………12分
……………12分
18.解:(1)∵![]() ,∴
,∴![]() , ……2分
, ……2分
∵函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,
,
∴![]() ,∴
,∴![]() ……………………………………………………5分
……………………………………………………5分
(2)∵点![]() 在直线
在直线![]() 上, ∴
上, ∴![]() ,∴
,∴![]() ,
,
∵![]() 在
在![]() 的图象上,∴
的图象上,∴![]() ,
,
∴![]() …………………………………………7分
…………………………………………7分
由(1)得:![]() ,
,
令![]() ,则
,则![]() ,因此函数
,因此函数![]() 的单调递增区间为(1,+∞),……9分
的单调递增区间为(1,+∞),……9分
令![]() ,则
,则![]() ,因此函数
,因此函数![]() 的单调递减区间为(-1,1)
的单调递减区间为(-1,1)
∴当![]() 时,函数
时,函数![]() 取得极小值
取得极小值![]() ………………………………………12分
………………………………………12分
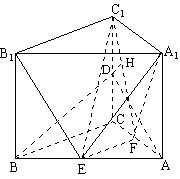
19.解:(1)在直三棱柱ABC—A1B1C1中,
 (1)∵
(1)∵![]() ,
,
∴![]() (或其补角)为异面直线AD与A1B1所成的角,
(或其补角)为异面直线AD与A1B1所成的角,
………………………2分,连结BD,
在![]() 中,∵AC=4,
中,∵AC=4,![]()
∴![]() ,
,
在![]() 中,∵BC=3,CD=2,∴
中,∵BC=3,CD=2,∴![]() ,
,
在△ABD中,∵AB=5,![]()
∴异面直线AD与A1B1所成角的余弦值为![]() ………………………………4分
………………………………4分
(2)证明:∵AB=5,BC=3,AC=4,∴![]() ,
,
∵底面ABC⊥侧面ACC1A1,∴BC⊥侧面ACC1A1,………………………………6分
取AB、AC的中点E、F,连结EF、A1F,则EF//BC,
∴EF⊥平面ACC1A1, ∴A1F为A1E在侧面AC1内的射影,
在正方形C1CAA1内,∵ D、F分别为CC1、AC的中点,
∴![]() ≌
≌![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() (三垂线定理)………………8分
(三垂线定理)………………8分
(3)连结![]() ,过D作DH⊥
,过D作DH⊥![]() ,垂足为H。
,垂足为H。
∵EF//BC,BC//B1C1,∴EF// B1C1,∴点F在平面B1C1E内。
∵EF⊥平面ACC1A1,![]() 平面ACC1A1,EF⊥DH,………………10分
平面ACC1A1,EF⊥DH,………………10分
∵![]() ,
,![]() ,∴DH⊥平面B1C1E。
,∴DH⊥平面B1C1E。
在![]() 中,∵
中,∵![]() ,∴
,∴![]() 。……………12分
。……………12分
20.解:(1)设从第一辆车投入施工算起,各车到达时间依此为![]() 、
、![]() 、…、
、…、![]() ,依题意,它们组成一个首项为0,公差为
,依题意,它们组成一个首项为0,公差为![]() (小时)的等差数列,…………3分
(小时)的等差数列,…………3分
则![]() =
=![]() +24d,∴
+24d,∴![]() =24×
=24×![]() =8,
=8,
答:第25辆车须8小时后才能到达。………………6分
(2)设从第一辆车投入施工算起,各车的工作时间依次为![]() 、
、![]() 、…、
、…、![]() ,依题意,它们组成一个公差为-
,依题意,它们组成一个公差为-![]() (小时)的等差数列,且
(小时)的等差数列,且![]() ………………8分
………………8分
∵每辆车每小时的工作效率为![]() ,∴
,∴![]()
即![]() ,……………………10分
,……………………10分
又∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
由于![]() ,可见
,可见![]() 的工作时间可以满足要求,即工程可以在24小时内完成。
的工作时间可以满足要求,即工程可以在24小时内完成。
答:24小时内能完成防洪堤坝。………………………………………………12分
21.(本小题满分12分)。
(1)解:依题意,可设所求抛物线方程为:![]()
则抛物线的准线方程为:![]() ,∴点M(2,y)到准线的距离
,∴点M(2,y)到准线的距离![]() ,……2分
,……2分
由抛物线定义知:![]() ,故
,故![]() ,∴
,∴![]() ,
,
故所求抛物线方程为:![]() 。………………4分
。………………4分
(2)证明:依题意,可设直线AB的方程为![]() ,代入抛物线方程
,代入抛物线方程![]() 得:
得:
![]() ,①
,①
设A、B两点的坐标分别是![]() 、
、![]() ,则
,则![]() 、
、![]() 是方程①的两根,
是方程①的两根,
∵![]() ,∴
,∴![]() ………………6分
………………6分
由点![]() 分有向线段
分有向线段![]() 所成的比为
所成的比为![]() 得:
得:![]() ,即
,即![]() ,
,
又点Q是点![]() 关于原点的对称点,故点Q的坐标是
关于原点的对称点,故点Q的坐标是![]() ,从而
,从而![]() ,
,
∵![]()
![]() ,
,
∴![]() …………………………………9分
…………………………………9分
![]()
![]()
![]() ,
,
∴![]() 。………………………………………12分。
。………………………………………12分。
22.解:(1)![]() ,
,
∵![]() ,∴
,∴![]() ,故当
,故当![]() 时,
时,![]() 。……………………………2分
。……………………………2分
若![]() ,∴
,∴![]() ,则
,则![]() ,∴
,∴![]()
若![]() ,则
,则![]() ,则
,则![]() ,∴
,∴![]() (舍去)
(舍去)
故![]() ……………………………………4分
……………………………………4分
(2)当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]()
∴![]() …………………………………………………6分
…………………………………………………6分
∴![]() ,
,
∴![]()
![]()
∴![]() ……………………………………………9分
……………………………………………9分
(3)∵![]() ……………………………………………10分
……………………………………………10分
∴![]() ,
,
∵![]() ,
,![]() ,…………
,…………
![]() ,
,
故当![]() 时,
时,![]() ,
,
因此,对任何常数A,设![]() 是不小于A的最小正整数,
是不小于A的最小正整数,
则当![]() 时,必有
时,必有![]() 。
。
故不存在常数A使![]() 对所有
对所有![]() 的正整数恒成立。……………………14分
的正整数恒成立。……………………14分