08届高考文科数学第四次月考测试

08届高考文科数学第四次月考测试试题

一、选择题：本大题共10小题，每小题5分，共50分　在每小题给出的四个选项中，只有一项是符合题目要求的　

1　已知集合M={y y=x+1}，N={(x，y)x ² +y ² =1}，则MN中元素的个数是（　 A ）

A　0　　　　　　 B　1　 　　　　C　2　　　　　 D　无穷个

2．函数在区间[1，2]上的最大值与最小值之和为，最大值与最小值之积为，则a等于（　 B　）

A　2　　　　　　 B　　　　　　C　2或　　　D　

3．已知实数a、b满足等式，下列五个关系式：　① 0<a<b<1；② 0<b<a<1； ③　a=b；④ 1<a<b；⑤　l<b<a　　其中不可能成立的关系式有（　B  ）

A　1个　　　　　 B　2个　　　　 C　3个　　　　D　4个

4．某校现有高一学生210人，高二学生270人，高三学生300人，学校学生会用分层抽样的方法从这三个年级的学生中随机抽取n名学生进行问卷调查，如果已知从高一学生中抽取的人数为7，那从高三学生中抽取的人数应为 （　A　）

　　　 A　10　　B　9　　　C　8　　　D　7

5. 若条件，条件，则是的(　B  )txjy

A．必要不充分条件　　　　　  B．充分不必要条件

C．充要条件　　　　　　　　  D．既不充分又不必要条件

6. 在等差数列中，则前n项和的最小值为(　 C　) txjy

A．　　　　 B．　　　　 C．　　　　　  D．

7. 已知x y满足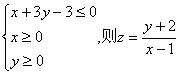的取值范围是　　　　 （　 B ）

　　A．[－2，1]　　　　　　　　　　　　　B．

　　　 C．[－1，2]　　　　 　　　　　　　　D．

8　函数在[2，+]上恒为正数，则实数a的取值范围是 （ C　）

　　A　0<a<1　　　　 B　1<a<2　　　　C　1<a< 　　 D　 2<a<3

9　连掷两次骰子分别得到点数m、n，则向量(m，n)与向量(－1，1)的夹角 的概率是（ D　 ）

　　A　　　　　　　B　　　　　　 C　 　　　　D　 

10. 已知圆,点,其中,是圆上的动点,的中垂线交所在直线于,则点的轨迹是　　　　　　　　　　 （ B　 ）

　　　 A．椭圆　 　 B．双曲线　　C．抛物线　 D．直线

11. 直线l过椭圆的中心，交椭圆于A、B两点，P是椭圆上的一点，若直线PA、PB的斜率分别为，则为（ C　）

　 A、　　  B、　　　　C、　　 D、不确定

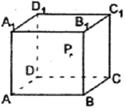12. 如右图所示，在正方体ABCD—A₁B₁C₁D₁的侧面AB₁内有一动点P到直线A₁B₁与直线BC的距离相等，则动点P所在曲线的形状为(　C )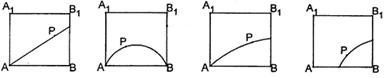

(A)　　　　　  (B)　　　　　  (C)　　　　　　 (D)

二、填空题（16分）

13．已知　 1　　　 。

14　已知函数在(－∞，+∞)上单调递减，则实数a的取值范围是______  ___________

15．已知，则=　　　　　 502　　　　　　　 

16．购买手机的“全球通”卡，使用时须付“基本月租费”(每月须交的固定月租费)50元，在市区通话时每分钟另收话费0　4元；购买“神州行”卡，使用时不收“基本月租费”，但市区内通话时每分钟另收话费0　6元　若某用户每月手机费预算为120元，则在这两种手机卡中，购买___神州行_______卡较合算

三、解答题（74分）

17．三角形ABC的角A、B、C所对的边分别是a，b，c。已知向量，且。

（1）　　　 求的值；

（2）　　　 若成等比数列，且，求的值。

解：由 得，

所以。

（2），

成等比数列，成等比数列

，又由余弦定理

，

又，所以或。

所以a，b，c分别为4，，6或6，，4。

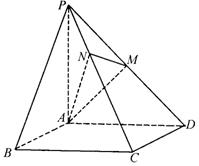
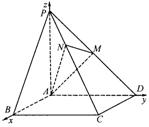
18．如图，已知四棱锥P—ABCD的底面是正方形，PA⊥底面ABCD，且PA=AD=2，点M、N分别在侧棱PD、PC上，且PM=MD　

　 （Ⅰ）求证：AM⊥平面PCD；

　 （Ⅱ）若，求平面AMN与平面PAB的所成锐二面角的大小　

解：（Ⅰ）因为四棱锥P—ABCD的底面是正方形，PA⊥底面ABCD，

则CD⊥侧面PAD　

又

又……………5分

　 （Ⅱ）建立如图所示的空间直角坐标系又PA=AD=2，

则有P（0，0，2），D（0，2，0）

设则有

同理可得

即得

由

而平面PAB的法微向量可为

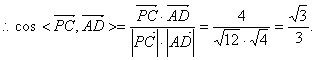
故所求平面AMN与PAB所成铰二面角的大小为

19．甲、乙两支足球队激战90分钟战成平局，加时赛30分钟后仍然为平局，先决定各派5名队员，每人射一点球决胜负。设甲、乙两队每个队员的点球命中率均为0.5。

（1）　　　 不考虑乙队，求甲对仅有3名队员点球命中，且其中恰有2名队员连续命中的概率；

（2）　　　 求甲、乙两队各射完5个点球后，再次出现平局的概率。

解：（1）甲队3名队员命中，恰有2名队员连续命中的情况有种，故所求概率为

（2）再次出现平局包括、6种情况，故其概率为=

20．已知函数f (x) = (x－a)(x－b)(x－c)　

(1) 求证：= (x－a)(x－b)+(x－a)(x－c)+(x－b)(x—c)；

(2) 若f (x)是R上的增函数，是否存在点P，使f (x)的图象关于点P中心对称?

如果存在，请求出点P坐标，并给出证明，如果不存在，请说明理由

21．已知等差数列满足：该数列的前三项分别加上1，1，3后顺次成为等比数列 的前三项

（Ⅰ）分别求数列，的通项公式

（Ⅱ）设若恒成立，求c的最小值　

解：（Ⅰ）设d、q分别为数列、数列的公差与公比，

由题可知，分别加上1，1，3后得2，2，+d,4+2d

是等比数列的前三项，

由此可得

（Ⅱ）①

当，当，②

①—②，得

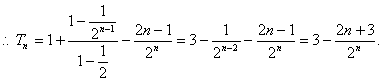
在N^*是单调递增的，

∴满足条件恒成立的最小整数值为

22．（本小题满分14分）已知抛物线的焦点为，过作两条互相垂直的弦、，设、的中点分别为

（1）　　　 求证：直线必过定点，并求出定点坐标  

（2）　　　 分别以和为直径作圆，求两圆相交弦中点的轨迹方程  

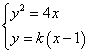解：（1）证明：由题可知，设，，直线AB的方程为，则由消去x可得

，

所以，，即，代入方程，解得，所以，点M的坐标为  

同理可得：的坐标为  

直线的方程为，整理得  

显然，不论为何值，均满足方程，所以直线恒过定点

（2）过作准线的垂线，垂足分别为  由抛物线的性质不难知道：准线为圆与圆的公切线，设两圆的相交弦交公切线于点，则由平面几何的知识（切割线定理）可知：为的中点  所以

，

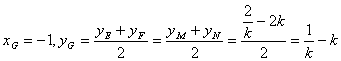即  

又因为公共弦必与两圆的连心线垂直，所以公共弦的斜率为

所以，公共弦所在直线的方程为

即

所以公共弦恒过原点  

根据平面几何的知识知道：公共弦中点就是公共弦与两圆连心线的交点，所以原点、定点、所求点构成以为直角顶点的直角三角形，即在以为直径的圆上  

又对于圆上任意一点（原点除外），必可利用方程求得值，从而以上步步可逆，故所求轨迹方程为