08届高考理科数学3月份质量检查(四)
数学(理)试卷
2008.3.10
YCY
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,满分150分,考试时间120分钟。
第I卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一项是符合题目要求的。
1.![]() ( )
( )
A.2 B.4 C.1 D.8
2.数列![]() 是首项为2005,公差为-3的等差数列,若
是首项为2005,公差为-3的等差数列,若![]() =1,则序号n等于 ( )
=1,则序号n等于 ( )
A.667 B.668 C.669 D.670
3.![]() ,则实数a的值为 ( )
,则实数a的值为 ( )
A.1 B.-1 C.1或-1 D.0或1或-1
4.若a、b为异面直线,给出以下结论:
(1)过空间内任何一点可以做一个和a、b都平行的平面
(2)过直线a有且只有一个平面和b平行
(3)过空间中任何一点可以作一条直线和a、b都相交
(4)有且只有一个平面经过a与b垂直
其中错误的个数为 ( )
A.0 B.1 C.2 D.3
5.过A(1,1)可作两条直线与圆![]() 相切,则k的范围为( )
相切,则k的范围为( )
A.k>0 B.k>4或0<k<1 C.k>4或k<1 D.k<0
6.已知x、y满足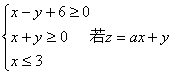 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() 则a的范围为 ( )
则a的范围为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.要得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象上所有的点(YCY)
的图象上所有的点(YCY)
A.横坐标缩短到原来的![]() 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移![]() 个单位长度
个单位长度
B.横坐标伸长到原来的2倍(纵坐标不变),再向左平移![]() 个单位长度
个单位长度
C.横坐标缩短到原来的![]() 倍(纵坐标不变),再向右平移
倍(纵坐标不变),再向右平移![]() 个单位长度
个单位长度
D.横坐标缩短到原来的2倍(纵坐标不变),再向右平移![]() 个单位长度
个单位长度
8.![]() 的最小值为 ( )
的最小值为 ( )
A.0 B.2 C.4 D.8
9.![]() 为奇函数且在[0,
为奇函数且在[0,![]() ]为减函数,则
]为减函数,则![]() 的一个值为
的一个值为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.![]() 的解为(
的解为(![]() ),则实数
),则实数![]() 和
和![]() 的乘积为 ( )
的乘积为 ( )
A.0 B.-3 C.-8 D.-12
11.已知F1、F2为双曲线![]() 的左、右焦点,P为右支上任意一点,若
的左、右焦点,P为右支上任意一点,若![]() 的最小值为8a,则该双曲线的离心率e的范围为 ( )
的最小值为8a,则该双曲线的离心率e的范围为 ( )
A.![]() B.
B.![]() C.[2,3] D.
C.[2,3] D.![]()
12.C为线段AB上一点,P为直线AB外一点,满足![]() ,
,![]()
![]()
![]() =( )
=( )
A.1 B.![]() C.
C.![]() D.2
D.2
第II卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分。
13.![]() 的解集为
的解集为
14.A(-2,0),B是圆F:(![]() )
)![]() 上的动点(F为圆心),线段AB的垂直平分线交直线BF于P,则动点P的轨迹方程为
上的动点(F为圆心),线段AB的垂直平分线交直线BF于P,则动点P的轨迹方程为
15.函数![]() 为增函数,则a的范围为
为增函数,则a的范围为
16.空间四边形ABCD,∠ABC=∠BCD∠CDA=![]() ,BC=CD=a,AB=AD=
,BC=CD=a,AB=AD=![]() ,A在面BCD上的射影为A1,若AA1中点为M,BC中点为N,过A、B、C、D四点的球的球心为O,若直线MN与球面交于P、Q两点,则∠POQ=
,A在面BCD上的射影为A1,若AA1中点为M,BC中点为N,过A、B、C、D四点的球的球心为O,若直线MN与球面交于P、Q两点,则∠POQ=
三、解答题:本大题共6小题,解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)YCY
已知A(2,0),B(0,2),C(![]() )
)
(1)若![]() 的值.
的值.
(2)若![]() 的值.
的值.
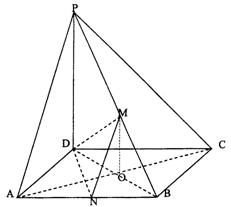
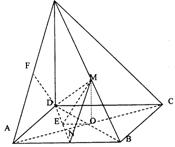
18.(本小题满分12分)
已知四棱锥P—ABCD的底面是边长为4的正方形,PD⊥面ABCD,PD=6,M,N分别
|
(1)证明:OM∥面PAD
(2)求二面角M—DN—C的平面角的正切值
(3)求点P到面DMN的距离
19.(本小题满分12分)
![]() 的最大值.
的最大值.
20.(本小题满分12分)
不等式组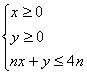 所表示的平面区域为Dn,若Dn内的整合个数为an,(整点即横坐标和纵坐标均为整数的点,
所表示的平面区域为Dn,若Dn内的整合个数为an,(整点即横坐标和纵坐标均为整数的点,![]() ).
).
(1)求数列![]() 的通项公式
的通项公式
(2)设数列![]() 的前n项和为Sn,且
的前n项和为Sn,且![]() 若对一切的正整数n,总有
若对一切的正整数n,总有![]() 成立,求m的范围.
成立,求m的范围.
21.(本小题满分14分)
已知![]() 成立, 设
成立, 设![]() ,
,
若![]() 、
、![]() 且
且![]() 成立.
成立.
求b的范围
22.(本小题满分14分)
过左焦点F1做倾斜角为60°的直线与椭圆![]() 交于A,B两点,
交于A,B两点,
与其左准线交于点P,若A为线段PB中点
(1)求椭圆的离心率e
(2)若![]() 为椭圆的右焦点,已知以F2为焦点,以过F1与x轴垂直的直线为准线的抛物线,过F1的直线与抛物线交于C、D两点,问,在x轴上是否存在一点E使得三角形CDE为等边三角形,若存在,求点坐标,若不存在,说明理由.
为椭圆的右焦点,已知以F2为焦点,以过F1与x轴垂直的直线为准线的抛物线,过F1的直线与抛物线交于C、D两点,问,在x轴上是否存在一点E使得三角形CDE为等边三角形,若存在,求点坐标,若不存在,说明理由.
参考答案
一、选择题
1.A 2.C 3.D 4.D 5.B 6.C 7.B 8.C 9.A 10.C 11.B 12.D
二、填空题
13.![]() 14.
14.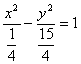 15.
15.![]() 16.
16.![]()
三、解答题
17.解:(1)![]() ∴C在线段AB的垂直平分线上,
∴C在线段AB的垂直平分线上,
∵AB的中点为(1,1),斜率为-1
∴线段AB的垂直平分线方程为![]()
∴![]()
∴![]() 又
又![]()
![]() ………………6分
………………6分
(2)![]()
∴![]()
∴![]()
∴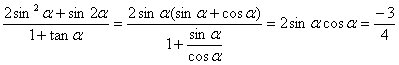 …………12分
…………12分
18.解:(1)∵BO=OD BM=MP ∴OM//PD
∵OM![]() 面PAD ∴OM//面PAD ………………2分
面PAD ∴OM//面PAD ………………2分
|
∴OM⊥面ABCD
过O做OE⊥ND于E,连接ME
则根据三垂线定理可得ME⊥ND
所以∠MEO为二面角M—DN—C的平面角
在△BDN中,BN=2,ND=2![]()
∴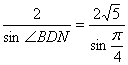 ∴
∴![]()
在Rt△OED中,OE=ODsin∠BDN=2![]()
∵![]()
![]() ………………7分
………………7分
(3)设P到面DMN的距离为h则![]()
![]()
∴AB⊥面PAD,∴面PAD⊥面PAB
所以过D做DF⊥PA于F,则DF⊥面PAD
∴![]()
∴P到面DMN的距离为![]() ………………12分
………………12分
19.解:![]() …………2分
…………2分
![]() 上为增函数
上为增函数
![]() ………………6分
………………6分

![]() ………………12分
………………12分
20.解(1)当![]()
![]()
![]() ………………4分
………………4分
(2)![]()
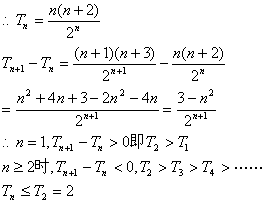
![]() ………………12分
………………12分
21.解:![]()
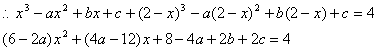
![]() ………………7分
………………7分
![]()
![]() 、
、![]() 成立.
成立.
![]() 在(0,3)上为增函数
在(0,3)上为增函数
所以![]()
因此![]()

![]() ………………14分
………………14分
22.解(1)过B做BB1垂直左准线于B1,过A做AA1垂直左准线于A1,过A做AA2垂直BB1于A2,则∠ABA2=60°
![]()
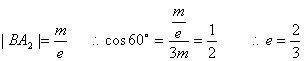 ………………6分
………………6分
(2)![]()
∴设抛物线方程为![]()
设直线CD的方程为![]()
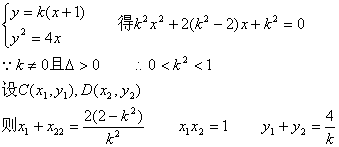
假设存在点E满足题意,设E(![]() )
)
设CD中点为M,则M![]()
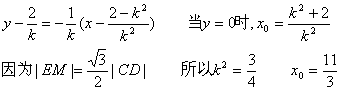
![]() ………………14分
………………14分