08届高考理科数学第二次模拟测试试题2
数学(理科)
注意事项:
1.本试卷分为选择题和非选择题两部分,共7页。
2.答卷前,考生务必将自己的姓名、座号、准考证号分别填写在答题卡及答题纸上。
3.选择题的每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号,不能答在试卷上。
4.考试结束后,将答题卡和答题纸一并交回。
第Ⅰ卷 选择题(共60分)
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合M=![]() ,N=
,N=![]() ,则集合
,则集合![]() =(
)
=(
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2.函数![]() 的最小正周期是( )
的最小正周期是( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.
![]()
3.若A、B、C是锐角三角形ABC的三个内角,向量![]() =(sinA,cosA),
=(sinA,cosA),
![]() =(sinB,−cosB),则
=(sinB,−cosB),则![]() 与
与![]() 的夹角为( )
的夹角为( )
A.锐角 B.直角 C.钝角 D.以上都不对
4.设函数f(x)是定义在R上的以3为周期的奇函数,若f(1)>1,f(2)=![]() ,则实数a的取值范围是( )
,则实数a的取值范围是( )
A.![]() B.
B.![]() 且
且![]() C.
C.![]() 或
或![]() D.
D.![]()
5. 在等差数列![]() 中,公差d=1,
中,公差d=1,![]() ,则
,则![]() 的值为( )
的值为( )
A.40 B.45 C.50 D.55
6.若P为双曲线![]() 右支上一点,P到右准线的距离为
右支上一点,P到右准线的距离为![]() ,则点P到双曲线左焦点的距离为( )
,则点P到双曲线左焦点的距离为( )
A.1 B.2 C.6 D.8
7.设函数y=arcsin![]() 的最大值为α,最小值为β,则sin(β-α)的值等于( )
的最大值为α,最小值为β,则sin(β-α)的值等于( )
A.![]() B.
B.![]() C.0 D.
C.0 D.![]()
8.非零向量![]() ,若点B关于
,若点B关于![]() 所在直线的对称点为
所在直线的对称点为![]() ,则向量
,则向量![]() 为( )
为( )
A、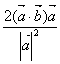 B、
B、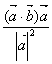 C、
C、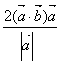 D、
D、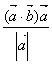
9.若实数x,y满足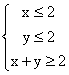 ,则x+2y的最小值和最大值分别为( )
,则x+2y的最小值和最大值分别为( )
A.2,6 B.2,5 C.3,6 D.3,5
10.在正三棱柱![]() 中,若
中,若![]() ,
,![]() ,则点
,则点![]() 到平面
到平面![]() 的距离为( ) (A)
的距离为( ) (A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
11.![]() ,且关于x的方程
,且关于x的方程![]() 有实根,则
有实根,则![]() 与
与![]() 夹角的取值范围是( )
夹角的取值范围是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、已知![]()
![]() = a ,且函数y=a
= a ,且函数y=a![]() +
+![]() +c在
+c在![]() 上存在反函数,则( )
上存在反函数,则( )
A、![]() B、
B、![]()
C、![]()
![]()
![]() D、
D、![]()
![]()
![]()
![]() 第Ⅱ卷 非选择题(共90分)
第Ⅱ卷 非选择题(共90分)
二.填空题(4×4′=16分):
13.![]() ;
;
14.已知n为等差数列−4,−2,0,…,中的第8项,则二项式![]() 展开式中的常数项是
;
展开式中的常数项是
;
15.若一个圆的圆心在抛物线![]() 的焦点上,且此圆与直线
的焦点上,且此圆与直线![]() 相
相
切,则这个圆的方程是 ;
16.已知m、n为直线,α,β为平面,给出下列命题:
①![]() ②
②![]() ③
③![]() ④
④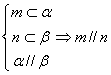
其中的正确命题序号是:
三.解答题(满分74分):
17(本题12分).设函数![]() 是奇函数.
是奇函数.
(Ⅰ)求![]() ;
;
(Ⅱ)求函数![]() (x∈
(x∈![]() )图象上每点切线斜率的取值范围.
)图象上每点切线斜率的取值范围.
18(本题12分).甲、乙两人同时参加一次面试,已知在备选的10道试题中,甲能答对其中的6道,乙能答对其中的8道,规定每次考试都从备选题中随机抽出3道题进行测试,至少答对2道题才算通过。求:
(Ⅰ)甲能答对的试题数ξ的概率分布与数学期望;
(Ⅱ)甲、乙两人至少有一人通过面试的概率.
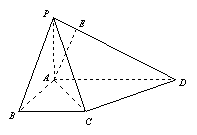 19(本题12分).如图,在四棱锥
19(本题12分).如图,在四棱锥![]() 中,底面
中,底面![]() 是一直角梯形,
是一直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 平面
平面![]() ,
,![]() 与底面成
与底面成![]() 角.
角.
(Ⅰ) 求证:平面![]() 平面
平面![]() ;
;
(Ⅱ) 求二面角![]() 的大小;
的大小;
(Ⅲ) 若![]() ,
,![]() 为垂足,求异面直线
为垂足,求异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
20(本题12分).函数![]() 过曲线y=f(x)上的点P(1,f(1))处的切线方程为y=3x+1
过曲线y=f(x)上的点P(1,f(1))处的切线方程为y=3x+1
(1)若y=f(x)在x=-2时有极值,求f(x)的表达式;
(2)若函数y=f(x)在区间![]() 上单调递增,求b的取值范围.
上单调递增,求b的取值范围.
21(本题12分).已知数列![]() 满足
满足![]() ,且
,且![]() .
.
(1)
求数列的前三项![]() ;
;
(2)
是否存在一个实数![]() ,使得数列
,使得数列![]() 为等差数列?若存在,求出
为等差数列?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)
若数列![]() 为等差数列,求数列
为等差数列,求数列![]() 的前n项和
的前n项和![]() ;
;
22(本题14分)已知双曲线C:![]() 的右准线与一条渐近线交于点M,F是右焦点,若
的右准线与一条渐近线交于点M,F是右焦点,若![]() ,且双曲线C的离心率e=
,且双曲线C的离心率e=![]() .
.
(1).求双曲线C的方程;
(2).过点A(0,1)的直线l与双曲线C的右支交于不同两点P、Q,且P在A、Q之间,若![]() 且
且![]() ,求直线l斜率k的取值范围
,求直线l斜率k的取值范围
(参考答案及评分细则)
一.选择题:DCADB DBAAB BC
二.填空题:13、![]() ,14、45,15、
,14、45,15、![]() 16、②、③
16、②、③
三.解答题:
17.解:(Ⅰ)∵![]() 为奇函数,∴
为奇函数,∴![]()
又![]() ,∴
,∴![]() …………………………………………(4分)
…………………………………………(4分)
(Ⅱ)y=x+cos3x+![]() =x+cos3x-sin3x=x+
=x+cos3x-sin3x=x+![]()
∴y′=1+3![]() ,……………………………………(8分)
,……………………………………(8分)
又∵x∈![]() ,∴
,∴![]() ∈
∈![]()
则y′∈(-2,4) ………………………………………………(12分)
18.解:(Ⅰ)P(ξ=0)=![]() =
=![]() ,P(ξ=1)=
,P(ξ=1)=![]() ,
,
P(ξ=2)=![]() ,P(ξ=3)=
,P(ξ=3)=![]() .……………………(3分)
.……………………(3分)
| ξ | 0 | 1 | 2 | 3 |
| P |
|
|
|
|
∴
则:Eξ=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() ……………………………(6分)
……………………………(6分)
(Ⅱ)甲未通过的概率为:p1=![]() ……………………(8分)
……………………(8分)
乙未通过的概率为:p2=![]() ……………………………(10分)
……………………………(10分)
∴甲、乙两人至少有一人通过面试的概率为:![]() =
=![]() …(12分)
…(12分)
19.(1)略(2)![]() (3)arccos
(3)arccos![]()
20.解:
由![]() 求导数得
求导数得![]() ,过y=f(x)上点P(1,f(1))处的切线方程为:
,过y=f(x)上点P(1,f(1))处的切线方程为:![]() 即y-(a+b+c+1)=(3+2a+b)(x-1),而过y=f(x)上P(1,f(1))的切线方程为:y=3x+1,故
即y-(a+b+c+1)=(3+2a+b)(x-1),而过y=f(x)上P(1,f(1))的切线方程为:y=3x+1,故![]() 即
即
![]()
![]() y=f(x)在x=-2时有极值,故
y=f(x)在x=-2时有极值,故![]()
![]()
由![]() 相联立解得
相联立解得![]() ,
,![]()
(2)![]() 在区间
在区间![]() 上单调递增
上单调递增
又![]() ,由(1)知
,由(1)知![]()
![]()
依题意![]() 在
在![]() 上恒有
上恒有![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
①在![]()
|
③在![]()
综合上述讨论可知,所求参数b取值范围是:b≥0……(14分)
21.解:(1)由题意知:![]() ,同理可得:
,同理可得:![]()
(2)假设存在实数![]() 符合题意,,则
符合题意,,则![]() 必为与n无关的常数,
必为与n无关的常数,![]() =
=![]() ,故
,故![]()
(3)由(2)知数列![]() 的公差d=1,得
的公差d=1,得![]() ,用错位相减法得:
,用错位相减法得:![]()
22.解:(1)由对称性,不妨设M是右准线![]() 与一渐近线
与一渐近线![]() 的交点,其坐标为M(
的交点,其坐标为M(![]() ),
),![]()
![]() ∴
∴![]() ,又
,又![]() ∴
∴![]() ,
,![]() ,解得
,解得![]() ,所以双曲线C的方程是
,所以双曲线C的方程是![]() ; (6分)
; (6分)
(2)设直线l的斜率为k,则l的方程为y=kx+1,点![]()
由![]() 得:
得:![]()
![]() l与双曲线C的右支交于不同的两点P、Q,∴
l与双曲线C的右支交于不同的两点P、Q,∴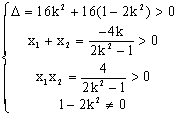
∴![]() 且
且![]() ①
(10分)
①
(10分)
又![]()
![]() 且P在A、Q之间,
且P在A、Q之间,![]() ,∴
,∴![]() 且
且![]() ,
,
∴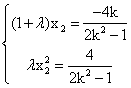 ∴
∴![]() ,
,![]()
![]()
=![]() 在
在![]() 上是减函数(
上是减函数(![]()
![]() ),∴
),∴![]() ,∴
,∴
![]() ,由于
,由于![]() ,∴
,∴![]() ② (12分)
② (12分)
由①②可得:![]() ,即直线l斜率取值范围为
,即直线l斜率取值范围为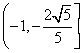 (14分)
(14分)