08届高考数学解析几何综合练习二
一、选择题
1.已知点A为双曲线![]() 的左顶点,点B和点C在双曲线的右支上,
的左顶点,点B和点C在双曲线的右支上,![]() 是等边三角形,则
是等边三角形,则![]() 的面积是
的面积是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.平面上整点(纵、横坐标都是整数的点)到直线![]() 的距离中的最小值是
的距离中的最小值是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.若实数x, y满足(x + 5)2+(y – 12)2=142,则x2+y2的最小值为
(A) 2
(B) 1
(C) ![]() (D)
(D)
![]()
4.直线![]() 椭圆
椭圆![]() 相交于A,B两点,该圆上点P,使得⊿PAB面积等于3,这样的点P共有
相交于A,B两点,该圆上点P,使得⊿PAB面积等于3,这样的点P共有
(A) 1个 (B) 2个 (C) 3个 (D) 4个
5.设a,b∈R,ab≠0,那么直线ax-y+b=0和曲线bx2+ay2=ab的图形是
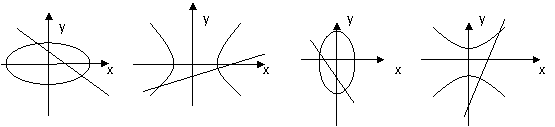 A
B
C
D
A
B
C
D
6.过抛物线y2=8(x+2)的焦点F作倾斜角为60o的直线,若此直线与抛物线交于A、B两点,弦AB的中垂线与x轴交于P点,则线段PF的长等于
A. ![]() B.
B. ![]() C.
C.![]() D.
D.![]()
7.方程![]() 表示的曲线是
表示的曲线是
A. 焦点在x轴上的椭圆 B. 焦点在x轴上的双曲线
C. 焦点在y轴上的椭圆 D. 焦点在y轴上的双曲线
二、填空题
8.在椭圆![]() 中,记左焦点为F,右顶点为A,短轴上方的端点为B。若该椭圆的离心率是
中,记左焦点为F,右顶点为A,短轴上方的端点为B。若该椭圆的离心率是![]() ,则
,则![]() =
。
=
。
9.椭圆![]() 的短轴长等于
。
的短轴长等于
。
10.设F1,F2是椭圆![]() 的两个焦点,P是椭圆上的点,且PF1 : PF2=2 : 1,则三角形
的两个焦点,P是椭圆上的点,且PF1 : PF2=2 : 1,则三角形![]() PF1F2的面积等于______________.
PF1F2的面积等于______________.
11.在平面直角坐标系XOY中,给定两点M(-1,2)和N(1,4),点P在X轴上移动,当![]() 取最大值时,点P的横坐标为___________________。
取最大值时,点P的横坐标为___________________。
12.若正方形ABCD的一条边在直线![]() 上,另外两个顶点在抛物线
上,另外两个顶点在抛物线![]() 上.则该正方形面积的最小值为 .
上.则该正方形面积的最小值为 .
三、解答题
13.已知![]() :
:![]() 和
和![]() :
:![]() 。试问:当且仅当a,b满足什么条件时,对
。试问:当且仅当a,b满足什么条件时,对![]() 任意一点P,均存在以P为顶点、与
任意一点P,均存在以P为顶点、与![]() 外切、与
外切、与![]() 内接的平行四边形?并证明你的结论。
内接的平行四边形?并证明你的结论。
14.设曲线C1:![]() (a为正常数)与C2:y2=2(x+m)在x轴上方公有一个公共点P。
(a为正常数)与C2:y2=2(x+m)在x轴上方公有一个公共点P。
(1)实数m的取值范围(用a表示);
(2)O为原点,若C1与x轴的负半轴交于点A,当0<a<![]() 时,试求⊿OAP的面积的最大值(用a表示)。
时,试求⊿OAP的面积的最大值(用a表示)。
15.已知点![]() 和抛物线
和抛物线![]() 上两点
上两点![]() 使得
使得![]() ,求点
,求点![]() 的纵坐标的取值范围.
的纵坐标的取值范围.
16.一张纸上画有半径为R的圆O和圆内一定点A,且OA=a. 拆叠纸片,使圆周上某一点A/ 刚好与A点重合,这样的每一种拆法,都留下一条直线折痕,当A/取遍圆周上所有点时,求所有折痕所在直线上点的集合.
17.在平面直角坐标系xoy中,给定三点![]() ,点P到直线BC的距离是该点到直线AB,AC距离的等比中项。
,点P到直线BC的距离是该点到直线AB,AC距离的等比中项。
(Ⅰ)求点P的轨迹方程;
(Ⅱ)若直线L经过![]() 的内心(设为D),且与P点的轨迹恰好有3个公共点,求L的斜率k的取值范围。
的内心(设为D),且与P点的轨迹恰好有3个公共点,求L的斜率k的取值范围。
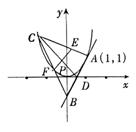
18.过抛物线![]() 上的一点A(1,1)作抛物线的切线,分别交
上的一点A(1,1)作抛物线的切线,分别交![]() 轴于D,交
轴于D,交![]() 轴于B.点C在抛物线上,点E在线段AC上,满足
轴于B.点C在抛物线上,点E在线段AC上,满足![]() ;点F在线段BC上,满足
;点F在线段BC上,满足![]() ,且
,且![]() ,线段CD与EF交于点P.当点C在抛物线上移动时,求点P的轨迹方程.
,线段CD与EF交于点P.当点C在抛物线上移动时,求点P的轨迹方程.
08届高考数学解析几何综合练习答案
1.C 2.B
3.B 4.B 5.B 6.A
7.C 8.90º 9.![]()
10.设椭圆的长轴、短轴的长及焦矩分别为2a、2b、2c,则由其方程知a=3,b=2,c=![]() ,故,PF1+PF2=2a=6,又已知[PF1:PF2=2:1,故可得PFl=4,PF2=2.在△PFlF2中,三边之长分别为2,4,2
,故,PF1+PF2=2a=6,又已知[PF1:PF2=2:1,故可得PFl=4,PF2=2.在△PFlF2中,三边之长分别为2,4,2![]() ,而22+42=(2
,而22+42=(2![]() )2,可见△PFlF2是直角三角形,且两直角边的长为2和4,故△PFlF2的面积=4.
)2,可见△PFlF2是直角三角形,且两直角边的长为2和4,故△PFlF2的面积=4.
11. 解:经过M、N两点的圆的圆心在线段MN的垂直平分线y=3-x上,设圆心为
S(a,3-a),则圆S的方程为:![]()
对于定长的弦在优弧上所对的圆周角会随着圆的半径减小而角度增大,所以,当![]() 取最大值时,经过M,N,P三点的圆S必与X轴相切于点P,即圆S的方程中的a值必须满足
取最大值时,经过M,N,P三点的圆S必与X轴相切于点P,即圆S的方程中的a值必须满足![]() 解得 a=1或a=-7。
解得 a=1或a=-7。
即对应的切点分别为![]() ,而过点M,N,
,而过点M,N,![]() 的圆的半径大于过点M,N,P的圆的半径,所以
的圆的半径大于过点M,N,P的圆的半径,所以![]() ,故点P(1,0)为所求,所以点P的横坐标为1。
,故点P(1,0)为所求,所以点P的横坐标为1。
12.解:设正方形的边AB在直线![]() 上,而位于抛物线上的两个顶点坐标为
上,而位于抛物线上的两个顶点坐标为![]() 、
、![]() ,则CD所在直线
,则CD所在直线![]() 的方程
的方程![]() 将直线
将直线![]() 的方程与抛物线方程联立,得
的方程与抛物线方程联立,得![]()
令正方形边长为![]() 则
则![]() ①
①
在![]() 上任取一点(6,,5),它到直线
上任取一点(6,,5),它到直线![]() 的距离为
的距离为![]() ②.
②.
①、②联立解得![]() 或
或![]()
13.利用极坐标解决:以坐标原点为极点,x轴为极轴建立极坐标系,则椭圆的极坐标方程为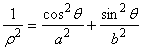 ------(1)
------(1)
显知此平行四边形ABCD必为菱形,设A![]() ,则B
,则B![]()
代入(1)式相加:![]()
由于该菱形必与单位圆相切,故原点到AB的距离为1,
∴![]() ,从而
,从而![]() ,∴
,∴![]()
14. 解:(1)由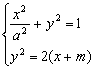 消去y得:
消去y得:![]() ①
①
设![]() ,问题(1)化为方程①在x∈(-a,a)上有唯一解或等根.
,问题(1)化为方程①在x∈(-a,a)上有唯一解或等根.
只需讨论以下三种情况:
1°△=0得:![]() ,此时xp=-a2,当且仅当-a<-a2<a,即0<a<1时适合;
,此时xp=-a2,当且仅当-a<-a2<a,即0<a<1时适合;
2°f (a)f (-a)<0,当且仅当-a<m<a;
3°f (-a)=0得m=a,此时xp=a-2a2,当且仅当-a<a-2a2<a,即0<a<1时适合.
f (a)=0得m=-a,此时xp=-a-2a2,由于-a-2a2<-a,从而m≠-a.
综上可知,当0<a<1时,![]() 或-a<m≤a;
或-a<m≤a;
当a≥1时,-a<m<a.……………………………………………… 10分
(2)△OAP的面积![]()
∵0<a<![]() ,故-a<m≤a时,0<
,故-a<m≤a时,0<![]() <a,
<a,
由唯一性得 ![]()
显然当m=a时,xp取值最小.由于xp>0,从而yp=![]() 取值最大,此时
取值最大,此时![]() ,∴
,∴![]() .
.
当![]() 时,xp=-a2,yp=
时,xp=-a2,yp=![]() ,此时
,此时![]() .
.
下面比较![]() 与
与![]() 的大小:
的大小:
令![]() ,得
,得![]()
故当0<a≤![]() 时,
时,![]() ≤
≤![]() ,此时
,此时![]() .
.
当![]() 时,
时,![]() ,此时
,此时![]() .……… 20分
.……… 20分
15.解:设![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() .
.
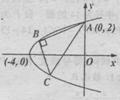 显然
显然![]() ,故
,故![]()
由于![]() ,所以
,所以![]()
从而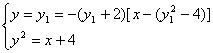 ,消去
,消去![]() ,注意到
,注意到![]() 得:
得:
![]()
![]()
![]()
由![]() 解得:
解得:![]() 或
或![]() .
.
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ;当
;当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,均满足是题意.故点
,均满足是题意.故点![]() 的纵坐标的取值范围是
的纵坐标的取值范围是![]() 或
或![]() .
.
16.解:如图,以O为原点,OA所在直线为x轴建立直角坐标系,则有A(a,0).设折叠时,⊙O上点A/(![]() )与点A重合,而折痕为直线MN,则 MN为线段AA/的中垂线.设P(x,y)为MN上任一点,则|PA/|=|PA| 5分
)与点A重合,而折痕为直线MN,则 MN为线段AA/的中垂线.设P(x,y)为MN上任一点,则|PA/|=|PA| 5分
∴![]()
即![]() 10分
10分
∴![]()
可得:![]()
∴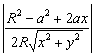 ≤1 (此不等式也可直接由柯西不等式得到) 15分
≤1 (此不等式也可直接由柯西不等式得到) 15分
平方后可化为 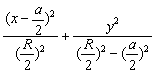 ≥1,
≥1,
即所求点的集合为椭圆圆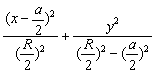 =1外(含边界)的部分. 20分
=1外(含边界)的部分. 20分
17. 解:(Ⅰ)直线AB、AC、BC的方程依次为![]() 。点
。点![]() 到AB、AC、BC的距离依次为
到AB、AC、BC的距离依次为![]() 。依设,
。依设,![]() ,即
,即![]() ,化简得点P的轨迹方程为
,化简得点P的轨迹方程为
圆S:![]() ......5分
......5分
(Ⅱ)由前知,点P的轨迹包含两部分
圆S:![]() ①
①
与双曲线T:![]() ②
②
因为B(-1,0)和C(1,0)是适合题设条件的点,所以点B和点C在点P的轨迹上,且点P的轨迹曲线S与T的公共点只有B、C两点。
![]() 的内心D也是适合题设条件的点,由
的内心D也是适合题设条件的点,由![]() ,解得
,解得![]() ,且知它在圆S上。直线L经过D,且与点P的轨迹有3个公共点,所以,L的斜率存在,设L的方程为
,且知它在圆S上。直线L经过D,且与点P的轨迹有3个公共点,所以,L的斜率存在,设L的方程为
![]() ③
③
(i)当k=0时,L与圆S相切,有唯一的公共点D;此时,直线![]() 平行于x轴,表明L与双曲线有不同于D的两个公共点,所以L恰好与点P的轨迹有3个公共点。......10分
平行于x轴,表明L与双曲线有不同于D的两个公共点,所以L恰好与点P的轨迹有3个公共点。......10分
(ii)当![]() 时,L与圆S有两个不同的交点。这时,L与点P的轨迹恰有3个公共点只能有两种情况:
时,L与圆S有两个不同的交点。这时,L与点P的轨迹恰有3个公共点只能有两种情况:
情况1:直线L经过点B或点C,此时L的斜率![]() ,直线L的方程为
,直线L的方程为![]() 。代入方程②得
。代入方程②得![]() ,解得
,解得![]() 。表明直线BD与曲线T有2个交点B、E;直线CD与曲线T有2个交点C、F。
。表明直线BD与曲线T有2个交点B、E;直线CD与曲线T有2个交点C、F。
故当![]() 时,L恰好与点P的轨迹有3个公共点。 ......15分
时,L恰好与点P的轨迹有3个公共点。 ......15分
情况2:直线L不经过点B和C(即![]() ),因为L与S有两个不同的交点,所以L与双曲线T有且只有一个公共点。即方程组
),因为L与S有两个不同的交点,所以L与双曲线T有且只有一个公共点。即方程组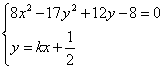 有且只有一组实数解,消去y并化简得
有且只有一组实数解,消去y并化简得![]()
该方程有唯一实数解的充要条件是![]() ④
④
或![]() ⑤
⑤
解方程④得![]() ,解方程⑤得
,解方程⑤得![]() 。
。
综合得直线L的斜率k的取值范围是有限集![]() 。 ......20分
。 ......20分
18.解一:过抛物线上点A的切线斜率为:![]() 切线AB的方程为
切线AB的方程为![]() 的坐标为
的坐标为![]() 是线段AB的中点. ………………5分
是线段AB的中点. ………………5分
设![]() 、
、![]() 、
、![]() 、
、![]() ,则由
,则由![]() 知,
知,
![]()
![]() 得
得![]()
 ∴EF所在直线方程为:
∴EF所在直线方程为: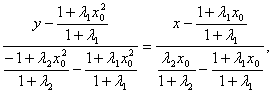
化简得![]() …①…………10分
…①…………10分
当![]() 时,直线CD的方程为:
时,直线CD的方程为:![]() …②
…②
联立①、②解得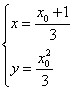 ,消去
,消去![]() ,得P点轨迹方程为:
,得P点轨迹方程为:![]() ………15分
………15分
当![]() 时,EF方程为:
时,EF方程为:![]() 方程为:
方程为:![]() ,联立解得
,联立解得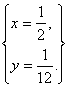 也在P点轨迹上.因C与A不能重合,∴
也在P点轨迹上.因C与A不能重合,∴![]()
∴所求轨迹方程为![]() ………………………………………………20分
………………………………………………20分
解二:由解一知,AB的方程为![]() 故D是AB的中点. ……5分
故D是AB的中点. ……5分
令![]() 则
则![]() 因为CD为
因为CD为![]() 的中线,
的中线,
![]()
而![]()
![]() 是
是![]() 的重心. ………………………………………………………………………10分
的重心. ………………………………………………………………………10分
设![]() 因点C异于A,则
因点C异于A,则![]() 故重心P的坐标为
故重心P的坐标为
![]() 消去
消去![]() 得
得![]()
故所求轨迹方程为![]() ………………………………………………20分
………………………………………………20分