高考数学数列专题练习

高考数学数列专题练习

一. 选择题

1．已知等差数列{a_n}的公差为2，若a₁,a₃,a₄成等比数列，则a₂=（　 ）
(A)-4　　 (B)-6　　 (C)-8　　　(D)-10

2．（2004，全国3，3）设数列是等差数列， ，S_n是数列的前n项和，则（　 ）

A.S₄＜S₅　 　　　　　　　　　　　B.S₄＝S₅ 　　　　　　　　　 C.S₆＜S₅　 　　　　　　　 D.S₆＝S₅

3．等比数列{a_n}中，a₂＝9，a₅＝243，则{a_n}的前4项和为( 　)

A81　　　　　　　　B120　　　　　　　　C168　　　　　　　　D192

4．设Sn是等差数列{a_n}的前n项和，若=，则=(　　)

A　1　　　B　 －1　　　 C　　2　　　 D　

5．等差数列中，，则此数列前20项和等于（　 ）

　　　 A．160 B．180　C．200 D．220

6．已知数列，那么“对任意的，点都在直线上”是“为等差数列”的（　　）

A. 必要而不充分条件　　　　　　　　　B. 充分而不必要条件

C. 充要条件　　　　　　　　　　　　　　　　　D. 既不充分也不必要条件

7．已知数列{}的前n项和

其中a、b是非零常数，则存在数列{}、{}使得（　　）

　　　 A．为等差数列，{}为等比数列

　　　 B．和{}都为等差数列

　　　 C．为等差数列，{}都为等比数列

　　　 D．和{}都为等比数列

8．数列（　 ）

　　　 A．　 B．　　C．　 D．（2004，湖南理，8）

9．若数列是等差数列，首项

，则使前n项和成立的最大自然数n是：（ 　　 ）

A　  4005　　　 B　4006　　　 C　　4007　　　  D　 4008

二. 填空题

1．设等比数列{a_n}(n∈N)的公比q=－,且

(a₁+a₃+a₅+…+a_2n-1)=,则a₁= _______ .

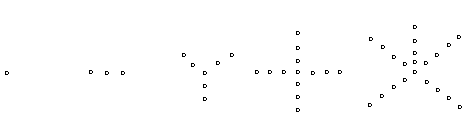2．根据下列5个图形及相应点的个数的变化规律，试猜测第个图中有_________个点.

（1）　　　　 （2）　　　　 （3）　　　　 （4）　　 　　 （5）

3．在等差数列中，当时，必定是常数数列。然而在等比数列中，对某些正整数、，当时，非常数数列的一个例子是________________________________________.

4．定义“等和数列”：在一个数列中，如果每一项与它后一项的和都为同一常数，那么这个数列叫做等和数列，这个常数叫做该数列的公和。

已知数列{ a_n}为等和数列，且a₁ =2，公和为5，那么a₁₈的值为_____________，这个数列的前n项和的计算公式为______________________________。

5．设数列{a_n}的前n项和为S_n，S_n=(对于所有n≥1)，且a₄=54，则a₁的数值是____________.

6．若干个能唯一确定一个数列的量称为该数列的“基本量”.设{a_n}是公比为q的无穷等比数列,下列{a_n}的四组量中,一定能成为该数列“基本量”的是第　　　　　 组.(写出所有符合要求的组号)

　　　　  ①S₁与S₂;　 ②a₂与S₃;　 ③a₁与a_n;　 ④q与a_n.

　 其中n为大于1的整数, S_n为{a_n}的前n项和.

三. 解答题

1．已知成公比为2的等比数列

(也成等比数列. 求的值.

2．设是一个公差为的等差数列，它的前10项和且，，成等比数列。

（1）证明；（2）求公差的值和数列的通项公式。

3．设数列满足

(1)　 　证明对一切正整数n 成立；

　令,判断的大小，并说明理由。

4．已知数列{a_n}的前n项和S_n满足：S_n=2a_n +(-1)ⁿ,n≥1.

⑴写出求数列{a_n}的前3项a₁,a₂,a₃；

⑵求数列{a_n}的通项公式；

⑶证明：对任意的整数m>4，有.