高考数学集合与简易逻辑分类选编
（集合与简易逻辑）
一、选择题
1．（重庆）已知
是
的充分不必要条件，
是的必要条件，
是的必要条
件．那么是成立的：（ ）
（A）充分不必要条件 （B）必要不充分条件
（C）充要条件 （D）既不充分也不必要条件
2．（北京）设全集是实数集R，
，
，则
等于（ ）
（A）
（B）
（C）
（D）
3．（天津）设集合
，
，那么下列结
论正确的是（ ）
（A）
（B）
（C）
（D）
4．（四川云南吉林黑龙江）
M＝
，N＝
，则集合Ｍ
Ｎ＝（
）
（A）{
}
（B）{
}
（C）{
}
（D）{
}
5．（湖北）设集合P＝
，Q＝
R
对任
意实数
恒成立，则下列关系中成立的是（
）
|
|
Q＝
6．（湖北）设A＝
，
Ｎ
，B＝
≤6，
Q，则AB等于（ ）
（A）{1,4} （B）{1,6} （C）{4,6} （D）{1,4,6}
7．（陕西广西海南西藏内蒙古）设集合M＝
,R，
R
，N＝
，R，R，则集合
中元素
的个数为 （ ）
（A）1 （B）2 （C）3 （D）4
8．（山东山西河南河北江西安徽）
设A、B、I均为非空集合，且满足A
BI，则下列各式中错误的是（
）
（A）（CIA）
B＝I （B）（CIA）（CIB）＝I
（C）A（CIB）＝ （D）（CIA）（CIB）＝CIB
9．（陕西广西海南西藏内蒙古）不等式
的解集为（
）
（A）
（B）
（C）
（D）
10．（福建）命题p：若
、
∈R，则
＞1是
＞1的充分而不必
要条件；命题q：函数
的定义域是（－
，
，＋
.
则（ ）
（A）“p或q”为假 （B）“p且q”为真
（C）p真q假 （D）p假q真
11．（浙江）“
”是“A=30º”的（ ）
（A）充分而不必要条件 （B）必要而不充分条件
（C）充分必要条件 （D）既不充分也必要条件
12．（重庆）不等式
的解集是（
）
（A）
（B）
（C）
（D）
13．（重庆）一元二次方程
有一个正根和一个负根的充分
不必要条件是（ ）
（A）
（B）
（C）
（D）
二、选择题
14．（山东山西河南河北江西安徽）不等式
≥
的解集是
．
15．（上海）设集合A＝｛5，
｝，集合B＝｛,｝．若AB＝
|
B＝ ．
16．（浙江）已知
＝
则不等式
≤5的解
集是 ．
17．（湖北）设A、B为两个集合，下列四个命题：
|
|
对任意
，有
②A B
|
|
A
B ④A B存在，使得
其中真命题的序号是 ．（把符合要求的命题序号都填上）
18．（江苏）二次函数
（∈R）的部分对应值如下表：
|
| －3 | －2 | －1 | 0 | 1 | 2 | 3 | 4 |
|
| 6 | 0 | －4 | －6 | －6 | －4 | 0 | 6 |
则不等式
＞0的解集是
．
三、解答题
19．（辽宁）
设全集U＝R
（1）解关于x的不等式
（
R）
（2）记A为（1）中不等式的解集，集合
B＝｛
｝，若
CU
恰有3个元素,
求a的取值范围．
参考答案
一、选择题
1．A 2．A 3．D 4．C 5．A 6．D 7．B 8．B 9．D 10．D 11．B
12．A 13．C
二、14．｛｜≥－1｝ 15．｛1，2，5｝ 16．（－，
17．（4）
18．
或
三、19．（1）由
＞0
＞
．
当
时，解集是R；
当
时，解集是
＜或＞
．
（2）当时，CU
＝；
当时，CU＝
．
因
＝
＝
．
由
，得
（Z），即
Z，所以B＝Z．
当CU恰有3个元素时，a就满足
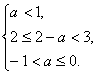解得
．