高考数学探析法向量在立体几何解题中的应用
一、用法向量求异面直线间的距离

![]()
![]() 如右图所示,a、b是两异面直线,
如右图所示,a、b是两异面直线,![]() 是 a E
是 a E
a和b 的法向量,点E∈a,F∈b,则
![]() 异面直线
a与b之间的距离是
异面直线
a与b之间的距离是
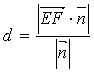 b F
b F
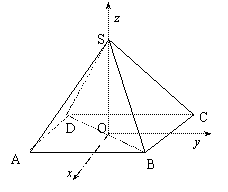 例1、如下图,正四棱锥S-ABCD的高SO=2,底边长
例1、如下图,正四棱锥S-ABCD的高SO=2,底边长![]() ,求异面直线BD和SC之间的距离.
,求异面直线BD和SC之间的距离.
分析:建立如图所示的直角坐标系,则
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.![]() ,
,
![]() .令向量
.令向量![]() ,且
,且![]() ,则
,则![]() ,
,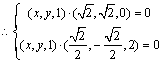 ,
,![]() ,
,![]() ,
,![]() .
.![]() 异面直线BD和SC之间的距离为:
异面直线BD和SC之间的距离为:
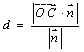
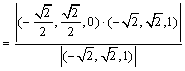
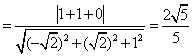 .
.
例2、如下图,正方体ABCD- A1B1C1D1的棱长为2,M、N分别为AA1,BB1的中点,
求(1)CM与D1N的余弦值;
(2)异面直线CM与D1N的距离。(2004年广州调研试题)
![]() 分析(2):建立如图所示右手直角坐标系,则C(0,2,0)、D1(0,0,2)、M(2,0,1)、N(2,2,1)
分析(2):建立如图所示右手直角坐标系,则C(0,2,0)、D1(0,0,2)、M(2,0,1)、N(2,2,1)
![]()

![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() D1
C1
D1
C1
![]()
![]()
![]() 设法向量
设法向量![]() A1 B1
A1 B1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 则 2x-2y+z=0
x=0 M D
N C
则 2x-2y+z=0
x=0 M D
N C
2x+2y-z=0 z=2y A B
![]()
![]() 令y=1得
令y=1得![]() ,依公式得异面直线CM与D1N的距离是
,依公式得异面直线CM与D1N的距离是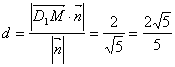
二、用法向量求点到平面的距离 A
![]()

![]() 如右图所示,已知AB是平面α的
如右图所示,已知AB是平面α的
![]()
![]()
![]()
![]() 一条斜线,
一条斜线,![]() 为平面α的法向量,则
C B
为平面α的法向量,则
C B
![]()
![]() A到平面α的距离为
A到平面α的距离为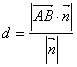 α
α
例3、已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在的平面,且GC=2,求点B到平面EFG的距离。
 分析:建立如图所示右手直角坐标系,
G
分析:建立如图所示右手直角坐标系,
G
![]()

![]()
![]()
![]()
![]()
![]()
![]() 则E(4,-2,0),F(2,-4,0),
E D
则E(4,-2,0),F(2,-4,0),
E D ![]() C
C
![]()
![]()
![]() G(0,0,2),B(4,0,0),
A F B
G(0,0,2),B(4,0,0),
A F B
![]() =(0,-2,0),
=(0,-2,0),![]() =(-4,2,2),
=(-4,2,2),![]() =(-2,4,2),设平面EFG的法向量
=(-2,4,2),设平面EFG的法向量![]() =(x,y,z),则由
=(x,y,z),则由![]() ,
,![]() 得
得
![]()
![]() -4x+2y+2z=0
x=
-4x+2y+2z=0
x= ![]()
![]() -2x+4y+2z=0
y=
-2x+4y+2z=0
y=![]()
不妨设z=3,则![]() =(1,-1,3),所以依公式可得所求距离为
=(1,-1,3),所以依公式可得所求距离为
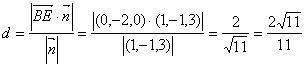
三、用法向量求直线到平面间的距离
首先必须确定直线与平面平行,然后将直线到平面的距离问题转化成直线上一点到平面的距离问题。
例4、已知边长为![]() 的正三角形ABC中,E、F分别为BC和AC的中点,PA⊥面ABC,且PA=2,设平面α过PF且与AE平行,求AE与平面α间的距离。
的正三角形ABC中,E、F分别为BC和AC的中点,PA⊥面ABC,且PA=2,设平面α过PF且与AE平行,求AE与平面α间的距离。
![]() 分析:因为AE∥平面α,所以将AE与平面α的距离转化成点A到平面α的距离,建立如图右手直角坐标系,
分析:因为AE∥平面α,所以将AE与平面α的距离转化成点A到平面α的距离,建立如图右手直角坐标系,
则A(0,0,0),P(0,0,2),
![]()
![]() E(
E(![]() ,0,0),F(
,0,0),F(![]() ,
,![]() ,0),
P
,0),
P
![]()

![]()
![]()
![]()
![]() ,
,![]() ,
A F
,
A F
![]()
![]() ,设法向量
,设法向量![]() =(x,y,z), B E C
=(x,y,z), B E C
则由![]() ,
,![]() 得,
得,
![]()
![]()
![]()
![]() x=0
x=0
![]()
![]()
![]() 不妨设防z=1,则
不妨设防z=1,则![]() =(0,
=(0,![]() ,1),所以依公式可得所求距离为
,1),所以依公式可得所求距离为
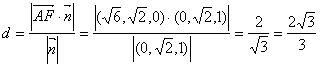
四、用法向量求两平行平面间的距离
首先必须确定两个平面是否平行,这时可以在一个平面上任取一点,将两平面间的距离问题转化成点到平面的距离问题。
例5、
棱长为![]() 的正方体
的正方体![]() 中.求证:平面AB1C∥平面
中.求证:平面AB1C∥平面![]() ;
;
(1)
 求平面
求平面![]() 与平面
与平面![]() 间的距离.
间的距离.
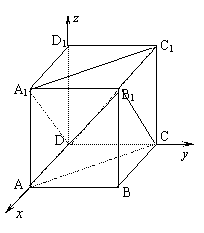
分析(2):建立如图所示的直角坐标系,
则A、D、A1、C1的坐标分别是
(1,0,0)、(0,0,0)、(1,0,1)、
(0,1,1),∴![]() ,
,
![]() ,
,![]() ,将平面
,将平面![]() 与平面
与平面![]() 间的距离转化成点A到平面
间的距离转化成点A到平面![]() 的距离。设平面
的距离。设平面![]() 的一个法向量
的一个法向量![]() ,
,
则![]() ,即
,即![]()
![]() ,
,
![]() ,
,![]() 平面
平面![]() 与平面
与平面![]() 间的距离
间的距离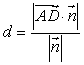
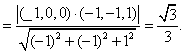
五、用法向量求二面角
如图,有两个平面α与β,分别作![]()
 这两个平面的法向量
这两个平面的法向量![]() 与
与![]() ,则平
,则平
![]()
 面α与β所成的角跟法向量
面α与β所成的角跟法向量![]() 与 α
与 α ![]()
![]()
![]()
![]()
![]()
![]() 所成的角相等或互补,所以首先
所成的角相等或互补,所以首先
![]() β
β
![]() 必须判断二面角是锐角还是钝角。
必须判断二面角是锐角还是钝角。
例6、如下图,在梯形ABCD中,AD∥BC,AB⊥BC,AB=a,AD=3a,sin∠ADC=![]() ,且PA⊥平面ABCD,PA=a,求二面角P-CD-A的平面角的余弦值。
,且PA⊥平面ABCD,PA=a,求二面角P-CD-A的平面角的余弦值。
![]()

![]()
![]() 分析:依题意,先过C点CE⊥AD,计算得ED=2a,BC=AE=a,建立如图右角直角坐标系,则P(0,0,a),D(0,3a,0), P
分析:依题意,先过C点CE⊥AD,计算得ED=2a,BC=AE=a,建立如图右角直角坐标系,则P(0,0,a),D(0,3a,0), P
C(a,a,0),![]() ,
A
E
D
,
A
E
D
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
B
C
,
B
C
![]()
![]()
![]()
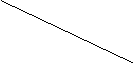
取平面ACD的一个法向量![]() ,设平面PCD的法向量是、
,设平面PCD的法向量是、![]() ,所以得
,所以得
![]()
![]()
![]()
![]()
![]()
![]()
![]()
所以不妨取得![]() ,从而计算得
,从而计算得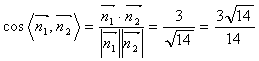
易得二面角P-CD-A的平面角是锐角,所以其角的余弦是![]()
六、用法向量求直线与平面所成的角
如图,要求直线a与平面α所成的角θ,先求这个平面α的法向量![]() 与直线a的夹角的余弦
与直线a的夹角的余弦![]() ,易知θ=
,易知θ=![]() 或者
或者![]()
![]() 例7、如下图,已知正四面体ABCD的边长为2,E为AD的中点,求EC与平面BCD所成的角。
例7、如下图,已知正四面体ABCD的边长为2,E为AD的中点,求EC与平面BCD所成的角。
![]()


 分析:作AO⊥平面BCD,连结OD,并且
A
分析:作AO⊥平面BCD,连结OD,并且
A
 过O作OF∥BC交CD于F,建立如图所
E
过O作OF∥BC交CD于F,建立如图所
E
![]()
![]() 示右手直角坐标系,则O(0,0,0),
B
O
D
示右手直角坐标系,则O(0,0,0),
B
O
D
![]()
![]()
![]()
![]()
![]() E(0,
E(0,![]() ,
,![]() ),
), ![]() C
F
C
F
易取得平面BCD上的一个法向量![]() ,所以
,所以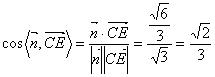 ,观察
,观察![]() 与
与![]() 的方向,易知EC与平面BCD所成的角是
的方向,易知EC与平面BCD所成的角是![]()
七、用法向量证明两平面平行问题
如果有一向量![]() 垂直于平面α,则向量
垂直于平面α,则向量![]() 叫做平面α的法向量。要证两个平面平行,只需证这两个平面同时垂直于它们的法向量。
叫做平面α的法向量。要证两个平面平行,只需证这两个平面同时垂直于它们的法向量。
例8、已知正方体ABCD-A1B1C1D1中,求证:平面A1BD∥平面B1D1C
![]() 分析:作如图所示右手直角坐标系,
D
C
分析:作如图所示右手直角坐标系,
D
C
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]() 则各点坐标是A1(1,0,0),
A
B
则各点坐标是A1(1,0,0),
A
B

![]()
![]()
![]() D1(0,0,0),B1(1,1,0),
D1 C1
D1(0,0,0),B1(1,1,0),
D1 C1
![]()
![]()
![]()
![]()
![]()
![]() B(1,1,1),D(0,0,1),
A1
B1
B(1,1,1),D(0,0,1),
A1
B1
![]() C(0,1,1) ,则
C(0,1,1) ,则![]() =(0,1,1),
=(0,1,1),
![]() =(-1,-1,0),设平面A1BD有一法向量
=(-1,-1,0),设平面A1BD有一法向量![]() =(x,y,z),则
=(x,y,z),则
![]()
![]() y+z
-x +-y =0
y+z
-x +-y =0
![]() x=z
y=-z
x=z
y=-z
不妨取z=1,则![]() =(1,-1,1) ,又由
=(1,-1,1) ,又由![]() =(-1,-1,0),
=(-1,-1,0),![]() =(0,1,1),易知
=(0,1,1),易知![]() =
=![]() ,
, ![]() =
=![]() ,所以
,所以![]() 与
与![]() 都与
都与![]() 垂直,所以
垂直,所以![]() 与平面B1D1C垂直,从而得到平面A1BD∥平面B1D1C
与平面B1D1C垂直,从而得到平面A1BD∥平面B1D1C
八、用法向量证明两平面垂直问题
要证两平面相互垂直,只需找出这两个平面的两个法向量,证明这两个法向量相互垂直。
例9、
![]() 如右图,△ABC是一个正三角形,EC⊥平面ABC,
如右图,△ABC是一个正三角形,EC⊥平面ABC,

![]()
![]() BD∥CE,且CE=CA=2BD,M是EA的中点。
E
BD∥CE,且CE=CA=2BD,M是EA的中点。
E
![]()

![]() 求证:(1)DE=DA;
M
D
求证:(1)DE=DA;
M
D
![]()
![]()
![]()
![]()
![]() (2)平面BDM⊥平面ECA;
C
B
(2)平面BDM⊥平面ECA;
C
B
(3)平面DEA⊥平面ECA; A
分析(3):建立如图所示右手直角坐标系
,不妨设CA=2,则CE=2,BD=1,C(0,0,0),A(![]() ,1,0),B(0,2,0),E(0,0,2),D(0,2,1),
,1,0),B(0,2,0),E(0,0,2),D(0,2,1),![]() ,
,![]() ,
,![]() , 分别假设面CEA与面DEA的法向量是
, 分别假设面CEA与面DEA的法向量是![]() 、
、![]() ,所以得
,所以得
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
不妨取![]() 、
、![]() ,从而计算得
,从而计算得![]() ,所以两个法向量相互垂直,两个平就相互垂直。
,所以两个法向量相互垂直,两个平就相互垂直。
事实证明,法向量在求角、距离以及证明平行垂直中都有非常广泛的应用,它在中学数学中的出现,是对传统的立体几何知识一个很好的补充及加深。