高考数学法向量在立几中的应用测试2

法向量在立体几何解题中的应用

一、 法向量的概念　 如果一个向量所在直线垂直于一个平面，则该向量是这个平面的一个法向量。

二、 法向量的作用

1、　证明线面平行　　取和直线平行的向量，验证该向量和法向量的数量积是否为零。

2 、 证明面面垂直　　验证两个平面的法向量的数量积是否为零。

3、求直线和直线所成的角　 若直线AB、CD所成的角是a，cosa=

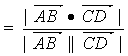
4 、 求直线和平面所成的角

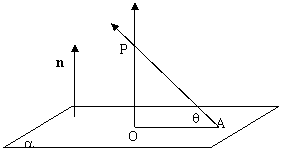
如图，已知PA为平面a的一条斜线，n为平面a的一个法向量，过P作平面a的垂线PO，连结OA则ÐPAO为斜线PA和平面a所成的角记为q，易得

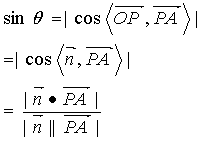
5　、求点到平面的距离

如图点P为平面外一点，点A为平面内的任一点，平面的法向量为n,过点P作平面a的垂

线PO，记∠OPA=q，则点P到平面的距离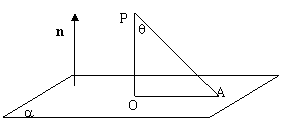

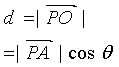
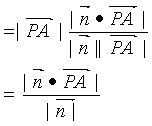
6　、求二面角的大小如图在二面角中，n₁和n₂分别为平面a和b的法向量，若二面角的大小为q，则=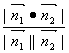(依据两平面法向量的方向或实际图形来确定q是锐角或是钝角)。