法向量在立体几何中的运用
孟志霞
河北省三河市第一中学 065200
在高中立体几何中引入了空间向量,大大降低了立体几何解题的难度.法向量的引入,对于解决空间的角与距离提供了很大的帮助.下面简单介绍法向量在立体几何中运用.
一、点到平面的距离.(先确定平面的法向量,再求点与平面上一点连结线段在平面的法向量上的射影长.设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,![]() 是平面
是平面![]() 外一点,
外一点,
![]() 是平面
是平面![]() 内一点,则点
内一点,则点![]() 到平面
到平面![]() 的距离
的距离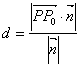 ).
).
例1.如图,在四棱锥![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,
且![]() ,
,![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
解:取![]() 的方向分别为
的方向分别为![]()
![]() 的正方向,建立空间直角坐标系,
的正方向,建立空间直角坐标系,
则![]() ,
,![]() ,
,![]()
![]()
![]() .
.![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]()
![]() ,
,![]() .所以可令
.所以可令![]() ,点
,点![]() 到
到
平面![]() 的距离
的距离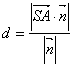 =
=![]() .
.
二、两条异面直线间的距离.(先求两条异面直线的一个公共法向量,再求两条异面直线上两点的连结线段在公共法向量上的射影长.设![]() 是异面直线,
是异面直线,![]() 是
是![]() 公共法向量,点
公共法向量,点![]() 则异面直线
则异面直线![]() 之间的距离
之间的距离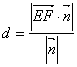 )。
)。
 例2.如图,已知
例2.如图,已知![]() 是正方形,
是正方形,![]() 平面
平面![]() ,
,![]() ,
,
![]() 分别是
分别是![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 之间的距离。
之间的距离。
![]() 解:以
解:以![]() 为原点,建立空间直角坐标系,
为原点,建立空间直角坐标系,![]()
![]()
![]() ,
,![]() ,
,![]()
![]() ,
,
![]() ,
,![]() ,
,![]() 是异面直线
是异面直线![]() 与
与![]() 的公共法向量,则
的公共法向量,则![]()
![]()
![]() 即
即![]()
![]()
![]() ;
;![]()
![]()
![]() 即
即![]()
![]()
![]()
![]() +
+![]() =0.所以
=0.所以![]() =
=![]() ,所以异面直线
,所以异面直线![]() 与
与![]() 之间的距离
之间的距离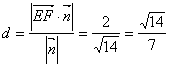 .
.
三、直线与平面的夹角.(求斜线与平面的法向量夹角的余角).
例3.如图,在直三棱柱![]() 中,底面是等腰直角三角形,
中,底面是等腰直角三角形,
![]() .侧棱
.侧棱![]() ,
,![]() 分别是
分别是![]() 与
与![]() 的中点,点
的中点,点![]() 在平面
在平面![]() 上的射影是
上的射影是![]() 的重心
的重心![]() .
.
![]() 求
求![]() 与平面
与平面![]() 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
![]() 求点
求点![]() 到平面
到平面![]() 的距离.
的距离.
(1)建立如图坐标系,设![]() ,则
,则![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,
,![]() 则
则![]() =
=![]() ,
,![]()
![]() ,
,![]()
![]()
![]() ,则
,则![]() =
=![]() ,
,![]() ,取平面
,取平面![]() 法向量为
法向量为![]() ,则
,则![]() 与
与![]() 夹角为
夹角为![]() 与平面
与平面![]() 所成角的余角.所以cos
所成角的余角.所以cos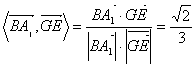 , 所以
, 所以![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
 (2)由(1)知
(2)由(1)知![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,即
,即![]() ,
,![]() 即
即![]() ,所以令法向量
,所以令法向量![]() .所以点
.所以点![]() 到平面
到平面![]() 的距离为
的距离为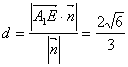 .
.![]()
四、两个平面的夹角.(求两个平面的法向量的夹角)。
例4.过正方形![]() 的顶点A,引
的顶点A,引![]() ,若
,若![]() ,
,
则平面![]() 与平面
与平面![]()
![]() 所成的二面角的大小.
所成的二面角的大小.
解:以![]() 为原点,
为原点,![]() 分别为
分别为![]() 轴
轴![]()
![]() 轴,
轴,![]() 轴建立空间直角坐标系如图。
轴建立空间直角坐标系如图。
则![]() ,
,![]() ,
, ![]() ,
, ![]() ,则
,则![]() ,
,![]() .设平面PCD的法向量为
.设平面PCD的法向量为![]() ,
,![]() ,即
,即![]() ;
;![]() ,即
,即![]() .所以可令
.所以可令![]() ;设平面PAB的法向量为
;设平面PAB的法向量为![]() ,所以平面PAB与平面PCD所成的二面角的余弦值为
,所以平面PAB与平面PCD所成的二面角的余弦值为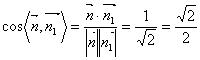 .所以平面
.所以平面![]() 与平面
与平面![]()
![]() 所成的二面角的平面角为
所成的二面角的平面角为![]() .
.
既然可以利用两个平面的法向量求两平面的夹角,也可以利用两个平面法向量证明两平面垂直.如下面的例5.可以先求两平面的法向量,再计算它们的数量积.
 例5.如图,正四棱柱
例5.如图,正四棱柱![]() 中,底面边长为
中,底面边长为![]() ,侧棱长为4,
,侧棱长为4,![]() 分别为棱
分别为棱![]() 的中点.
的中点.
求证:平面![]() 平面
平面![]()
![]() 解:以
解:以![]() 为原点,
为原点,![]() 分别
分别
为![]() 建立空间直角坐标系,则
建立空间直角坐标系,则![]() ,
,![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,
设平面EF的法向量为![]() ,
,
则![]()
![]() =0;
=0;![]() 即
即![]() .所以令
.所以令![]() =
=![]()
设平面![]() 的法向量为
的法向量为![]() =
=![]() ,
,![]()
![]() ,即4
,即4![]() =0;
=0; ![]()
![]() ,即
,即![]() .所以可令
.所以可令![]() .
.![]()
![]()
![]()
![]() =0
=0
![]() 平面
平面![]() 平面
平面![]() .
.