第四章 三角函数
[内容提要]
需要掌握三角函数的定义、三角函数值的符号、三角函数线的概念;熟记特殊角的角函数值,注重运用单位圆分析问题、解决问题;熟记同角三角函数间的基本关系式及诱导公式;掌握基本三角函数图象的画法、定义域、值域、周期的求法,以及奇偶性、最值点、单调区间、零点和对称点。
基本类型
(1) 角的度量:角度制、弧度制及角度与弧度的互化方面;
(2) 角的表示:象限角和终边相同角的集合表示;
(3) 同角三角函数间的基本关系:倒数关系、商数关系、平方关系;
(4) 诱导公式:奇变偶不变,符号看象限;
(5) 三角函数的图象与性质:定义域、值域、周期性、奇偶性、单调性、对称性。
(6)
![]() 的图象和性质:五点法、图象变换法、以图识性、数形结合;
的图象和性质:五点法、图象变换法、以图识性、数形结合;
(7) 三角函数线:利用三角函数线表示三角函数值的有向线段,及探求三角函数的变化规律,比较三角函数值的大小,解三角不等式。
一、概念及任意角的三角函数
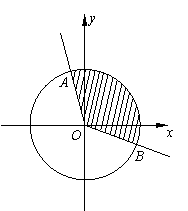 例1 如图4-1,射线
例1 如图4-1,射线![]() 与
与![]() 轴正方向所夹的锐角是
轴正方向所夹的锐角是![]() ,射线
,射线![]()
与![]() 轴正方向所夹的锐角是
轴正方向所夹的锐角是![]()
(1) 用弧度制写出![]() 内的阴影部分的角的集合(含边界);
内的阴影部分的角的集合(含边界);
(2) 用弧度制写出R上的阴影部分的角的集合(含边界).
例2 已知![]() 是第二象限的角,试判断下列各角的范围:
是第二象限的角,试判断下列各角的范围:
(1) ![]() ; (2)
; (2) ![]() ; (3)
; (3) ![]() .
.
例3 已知在角![]() 的终边上的一点
的终边上的一点![]()
![]() 求
求![]() 的值.
的值.
例4 求下列函数的定义域:
(1) ![]() ; (2)
; (2) ![]() .
.
例5 (1) 求函数![]() 的值域;
的值域;
(2) 如果![]() 是第三象限的角,判断
是第三象限的角,判断![]() 的符号;
的符号;
(3) 设![]() 是第四象限的角,比较
是第四象限的角,比较![]() 和
和![]() 的大小.
的大小.
基础过关
1. 已知命题: (1)终边相同的角必相等, (2)第一象限的角是锐角; (3)小于![]() 的角是锐角.
的角是锐角.
上述命题中,正确的个数是( )
(A) 0 (B) 1 (C) 2 (D) 3
2. ![]() 为第二象限的角,其终边上的一点为
为第二象限的角,其终边上的一点为![]() ,且
,且![]() ,则
,则![]() 等于( )
等于( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
3. 在![]() 到
到![]() 之间与
之间与![]() 的终边相同的角有___________.
的终边相同的角有___________.
4. 若![]() 是第三象限角,则
是第三象限角,则![]() 是__________象限角;
是__________象限角; ![]() 的范围是_____________;
的范围是_____________;
![]() 是__________象限角.
是__________象限角.
5. 已知角![]() 的终边上一点
的终边上一点![]() 到
到![]() 轴的距离与到
轴的距离与到![]() 轴的距离之比为
轴的距离之比为![]() ,且
,且![]() ,求
,求![]() 和
和![]() 的值.
的值.
6. 已知一扇形的周长为定值![]() .当扇形的中心角为多大时,他有最大的面积.
.当扇形的中心角为多大时,他有最大的面积.
能力迁移
7. 若![]() 是第二象限角,那么
是第二象限角,那么![]() 的值一定是( )
的值一定是( )
(A) 正数. (B) 负数.
(C) 正数、负数都有可能. (D) 正数、零都有可能.
8. 已知集合![]() 则
则![]() 与
与![]() 的关系
的关系
是( )
(A) ![]() . (B)
. (B) ![]()
![]()
![]() .
(C)
.
(C) ![]()
![]()
![]() .
(D)
.
(D) ![]() .
.
9. 用弧度制表示第四象限角的集合是____________.
10. 已知集合![]() 则
则![]()
_____________.
11. 已知角![]() 的顶点在原点,始边与
的顶点在原点,始边与![]() 轴的非负半轴重合,终边在直线
轴的非负半轴重合,终边在直线![]() 上.
上.
求![]() 的值.
的值.
12. 时针指到3点后,当分针在1小时内走55分时,时针到分针的角是多少度? 合多少弧度?
13. 求函数![]() 的定义域.
的定义域.
二、同角三角函数关系及诱导公式
基本知识
1. 同角三角函数间的基本关系:
倒数关系:![]() ,
,![]() ,
,![]()
商数关系:![]() ,
,![]() .
.
平方关系:![]() ,
,![]() ,
,![]()
补充:![]()
2. 诱导公式:(![]()
![]() 与
与![]() 的关系 )
的关系 )
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
奇变 奇变
例1 (1)![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)已知![]() 的内角A满足
的内角A满足![]() ,
,![]() ,求
,求![]() 的值。
的值。
例2 化简(1)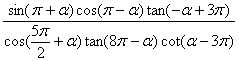 ;
;
(2)![]() .
.
例3 已知![]() ,且
,且![]() ,求(1)
,求(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
例4 若![]() ,且适合等式
,且适合等式![]() ,求
,求![]() 的取值范围.
的取值范围.
基础过关
1.化简![]() 的结果是( )
的结果是( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
2.![]() 的值是( )
的值是( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
3.已知![]() ,则
,则![]() .
.
4.已知![]() 是第四象限角,则
是第四象限角,则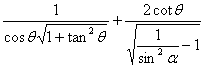 的值是 .
的值是 .
5.已知![]() ,
,![]() ,求
,求![]() 的值.
的值.
6.已知![]() ,求
,求![]() 的值.
的值.
能力迁移
7.设![]() 为
为![]() 的三内角,则不管
的三内角,则不管![]() 的形状如何变化,表达式
的形状如何变化,表达式
①![]() , ②
, ②![]() ;
;
③![]() ;
④
;
④![]()
始终表示常数的是( )
(A) ①与②. (B) ②与③. (C) ②与④. (D) ③与④.
8.设![]() ,其中
,其中![]() 都是非零实数.
都是非零实数.![]() ,那么
,那么![]() 等于( )
等于( )
(A) -1. (B) 0. (C) 1. (D) 2.
9.设![]() ,
,![]() ,那么
,那么![]() __________.
__________.
三、两角和与差的三角函数
1.基本公式
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
例1 填空题:
(1) ![]() 的值等于___________;
的值等于___________;
(2) ![]() ___________;
___________;
(3) ![]() __________.
__________.
例2 设![]() ,
,![]() 是第二象限的角,求
是第二象限的角,求![]() 的值.
的值.
例3 化简![]() .
.
例4 不查表求![]() 的值.
的值.
例5 (1) 求![]() 的值;
的值;
(2) 已知![]() ,求证
,求证![]() ,进而化简
,进而化简![]() .
.
基础过关
1.化简![]() 的结果是( )
的结果是( )
(A) ![]() . (B)
. (B) ![]() . (C)
. (C)
![]() . (D)
. (D)
![]() .
.
2.![]() ,则
,则![]() 的大小关系是( )
的大小关系是( )
(A) ![]() . (B)
. (B) ![]() .
(C)
.
(C) ![]() . (D)
. (D) ![]() .
.
3.已知![]() ,则
,则![]() __________.
__________.
4.已知![]() ,
,![]() ,则
,则![]() _________.
_________.
5.在斜三角形![]() 中,求证:
中,求证:![]() .
.
6.已知![]() ,求
,求![]() 的值.
的值.
能力迁移
7.![]() 等于( )
等于( )
(A) ![]() . (B)
. (B) ![]() .
(C)
.
(C) ![]() . (D)
. (D)
![]() .
.
8.![]() 等于( )
等于( )
(A) ![]() . (B)
. (B) ![]() .
(C)
.
(C) ![]() . (D)
2.
. (D)
2.
9.![]() ___________.
___________.
10.已知![]() ,化简
,化简![]() __________
__________![]() .
.
11.求证:![]() .
.
12.已知![]() ,求
,求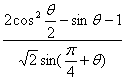 的值.
的值.
13.已知![]() 和
和![]() 是方程
是方程![]() 的两根,试求
的两根,试求![]() 满足的关系式.
满足的关系式.