圆锥曲线的基本问题
一、圆锥曲线的方程,参数之间的关系的问题.
1.椭圆![]() (a>b>0)的左焦点F到过顶点A(-a, 0), B(0,b)的直线的距离等于
(a>b>0)的左焦点F到过顶点A(-a, 0), B(0,b)的直线的距离等于![]() ,则椭圆的离心率为( ).
,则椭圆的离心率为( ).
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
分析:本题条件不易用平面几何知识转化,因而过A、B的方程为![]() ,左焦点F(-c,0),则
,左焦点F(-c,0),则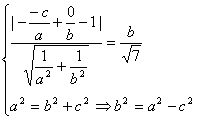 ,化简,得5a2-14ac+8c2=0
得
,化简,得5a2-14ac+8c2=0
得![]() 或
或![]() (舍), ∴ 选A.
(舍), ∴ 选A.
小结:应熟悉各方程的标准形式及各参数之间的关系和几何意义.若题面改为“双曲线![]() (a>b>0)”,则由“a>b>0”这个隐含条件可知离心率e的范围限制,即a>b>0,∴ a2>b2, ∴a2>c2-a2
从而
(a>b>0)”,则由“a>b>0”这个隐含条件可知离心率e的范围限制,即a>b>0,∴ a2>b2, ∴a2>c2-a2
从而![]() .
.
2.若双曲线的渐近线方程为![]() ,则其离心率为( ).
,则其离心率为( ).
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
分析:当双曲线方程为![]() 时,其渐近线为
时,其渐近线为![]() ,当双曲线方程为
,当双曲线方程为![]() 时,其渐近线为
时,其渐近线为![]() ,从而本题对应
,从而本题对应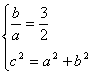 或
或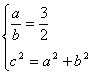 ,选D.
,选D.
3.若![]() 表示焦点在y轴上的双曲线,则它的半焦距的取值范围是( ).
表示焦点在y轴上的双曲线,则它的半焦距的取值范围是( ).
A、(1,+¥) B、(0,1) C、(1,2) D、与k有关
分析:首先应把方程标准化,方程可化为:
![]()
∴ 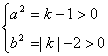 , ∴ k>2 c2=a2+b2=k-1+k-2=2k-3>2×2-3=1∴ c>1,选A.
, ∴ k>2 c2=a2+b2=k-1+k-2=2k-3>2×2-3=1∴ c>1,选A.
4.抛物线y2-2by+b2+4m-mx=0的准线与双曲线![]() 的右准线重合,则m的值为______.
的右准线重合,则m的值为______.
分析:首先将方程化为标准方程(y-b)2=m(x-4)
而双曲线![]() 的右准线为x=3, 抛物线顶点(4,b)在x=3的右侧,
的右准线为x=3, 抛物线顶点(4,b)在x=3的右侧,
∴ 抛物线开口向右,m>0, 2p=m,∴ 焦准距(焦参数)![]() ,∴m=4.
,∴m=4.
5.以3x-4y-2=0, 3x+4y-10=0为渐近线,以5y+4=0为一条准线的双曲线方程为_____.
分析:注意两条渐近线的交点,或一条渐近线和一条对称轴的交点都是双曲线的中心.
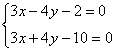 ,中心为(2,1),从而准线
,中心为(2,1),从而准线![]() 为下准线,焦点在平行于y轴的直线上,从而,中心与准线相矩
为下准线,焦点在平行于y轴的直线上,从而,中心与准线相矩![]() ……①,渐近线斜率为
……①,渐近线斜率为![]() ……②
……②
联立①②,得a=3,
b=4, c=5.方程为![]() .
.
6.若椭圆![]() (a>b>0)与圆
(a>b>0)与圆![]() 相交,则椭圆的离心率的取值范围为_______.
相交,则椭圆的离心率的取值范围为_______.
分析:圆锥曲线间的位置关系不能用联立方程,用判别式判定,一般来说应结合图形分析.
由图可知圆半径r满足 b<r<a,
∴ 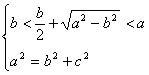 , 解得
, 解得![]() .
.
7.若双曲线![]() 与圆x2+y2=1无公共点则k∈______.分析:同上题用数形结合的方法知
与圆x2+y2=1无公共点则k∈______.分析:同上题用数形结合的方法知![]() 或
或![]() .
.
二、利用曲线定义求解的问题
1.双曲线的虚轴长为4,离心率![]() ,F1、F2分别是它的左,右焦点,若过F1的直线与双曲线的左支交于A、B两点,且AB是AF2与BF2的等差中项,则AB为( ).
,F1、F2分别是它的左,右焦点,若过F1的直线与双曲线的左支交于A、B两点,且AB是AF2与BF2的等差中项,则AB为( ).
A、![]() B、
B、![]() C、
C、![]() D、8
D、8
分析:利用双曲线定义, ∵ AB在左支上,∴AF2-AF1=2a, BF2-BF1=2a ∴ AF2+BF2-(AF1+BF1)=4a, 又∵ 2AB=AF2+BF2, AF1+BF1=AB
∴ 2AB-AB=4a. AB=4a,而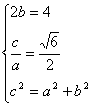 得
得![]() , ∴
, ∴ ![]() ,选A.
,选A.
2.设F1、F2为椭圆两焦点,点P是以F1,F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1,则椭圆离心率为( ).
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
分析:P在以F1F2为直径的圆上,则∠F1PF2=90°,
而∠PF1F2=5PF2F1,∴
∠PF1F2=75°, ∠PF2F1=15°,∴ ![]() ,
,
![]() ,而PF2+PF2=2a,∴
,而PF2+PF2=2a,∴ ![]() .
.
3.F1、F2为椭圆两个焦点,Q为椭圆上任一点,以任一焦点作∠F1QF2的外角平分线的垂线,垂足为P,则P点轨迹为( ).
A、圆 B、椭圆 C、双曲线 D、抛物线
分析:延长F2P交F1Q的延长线为M,由椭圆定义及角平分线,
∵ 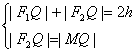 ∴
F1Q+MQ=F1M=2a,则点M(x0,y0)的轨迹方程为
∴
F1Q+MQ=F1M=2a,则点M(x0,y0)的轨迹方程为![]() ......① 设P点坐标(x, y), ∵ P为F2M中点,
......① 设P点坐标(x, y), ∵ P为F2M中点,
∴ 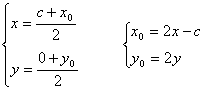 ,代入①,得 (2x-c+c)2+(2y)2=4a2,
∴ x2+y2=a2, 选A.
,代入①,得 (2x-c+c)2+(2y)2=4a2,
∴ x2+y2=a2, 选A.
4.双曲线![]() 的左支上一点P,⊙O'为ΔPF1F2的内切圆,则圆心O'的横坐标为(
).
的左支上一点P,⊙O'为ΔPF1F2的内切圆,则圆心O'的横坐标为(
).
A、a
B、-a
C、![]() D、
D、![]()
分析:设PF1,PF2,F1F2与内切圆⊙O'的切点分别为M,N,Q,由双曲线定义,
∵ PF2-PF1=2a, ∴ PN+NF2-(PM+MF1)=2a,
而 DN=PM ,MF1=QF1, NF2=QF2 ∴ QF2-QF1=2a 又 QF2+QF1=2c,∴ QF2=a+c=c-xQ, ∴ xQ=-a, ∵O'Q⊥F1F2, ∴xQ'=xQ=-a, 选B.
三、求曲线方程
1.待定系数法
例:已知椭圆D:![]() 与圆:x2+(y-m)2=9(m∈R),双曲线G与椭圆D有相同焦点,它的两条渐近线恰好与圆M相切.1)当m=5时,求双曲线G的方程.
与圆:x2+(y-m)2=9(m∈R),双曲线G与椭圆D有相同焦点,它的两条渐近线恰好与圆M相切.1)当m=5时,求双曲线G的方程.
2)当m取何值时,双曲线的两条准线间的距离为1.
解:1)椭圆D的两个焦点F1(-5,0),F2(5,0),因而双曲线中心在原点,焦点在x轴上,且c=5.
设双曲线G的方程为![]() ∴ 渐近线为bx±ay=0且a2+b2=25,
∴ 渐近线为bx±ay=0且a2+b2=25,
m=5时,圆心M(0,5), r=3.∴ ![]() , 得 a=3, b=4, ∴G方程为
, 得 a=3, b=4, ∴G方程为![]() .
.
2)双曲线两准线间距离为![]() , ∴
, ∴ ![]() ,
,
∵ G的渐近线与M相切, ∴ ![]() ,∴
,∴ ![]() .
.
2.相关点求轨迹法(代入法)
例:设抛物线过定点A(0,2),且以x轴为准线求抛物线顶点M的轨迹C的方程.
分析:A(0,2)在抛物线上,体现为
①A(0,2)的坐标满足曲线方程
②A(0,2)满足曲线定义
在本题中以方式②为佳,设M(x, y),焦点F(x0, y0),
∵ AF=![]() ,∴
,∴ ![]() , ∴
, ∴ ![]() ......①
......①
而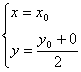 , ∴
, ∴ 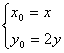 代入① ∴ x2+(2y-2)2=4,
代入① ∴ x2+(2y-2)2=4, ![]() 且 y≠0.
且 y≠0.
3.直接法(直接到方程化简)
例:设点O为原点,点M在直线l: x=-p(p>0)上移动,动点N在线段MO的延长线上,且满足MN=MO·NO. 求动点N的轨迹方程.
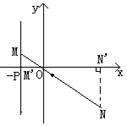 解:设N坐标为(x, y),过N作NN'⊥x轴于N',
解:设N坐标为(x, y),过N作NN'⊥x轴于N',
∵ M,O,N共线,
∴ ![]() , 由已知 MN=MO·NO
, 由已知 MN=MO·NO
∴ ![]()
∴ 所求方程为(p2-1)x2+p2y2-2px-p2=0(x>0)
4.直接法(直接利用曲线定义)
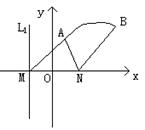 例:如图,直线l1, l2相交于M,l1⊥l2,点N∈l1, 以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等,若ΔAMN为锐角Δ,
例:如图,直线l1, l2相交于M,l1⊥l2,点N∈l1, 以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等,若ΔAMN为锐角Δ,![]() , AN=3,BN=6,建立适当坐标系,求曲线段C的方程.
, AN=3,BN=6,建立适当坐标系,求曲线段C的方程.
分析:以l1为x轴,以MN的中垂线为y轴建立直角坐标系,如图.
由题意,曲线段C是以N为焦点,以l2为准线的抛物线的一部分,
其中A、B分别为C的端点.
由已知条件,可求方程为y2=8x(1≤x≤4, y>0)(过程略)
5.交轨法
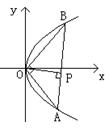 例:抛物线y2=2px(p>0),O为坐标原点,A、B在抛物线上,且OA⊥OB,过O作OP⊥AB交AB于P,求P点轨迹方程.
例:抛物线y2=2px(p>0),O为坐标原点,A、B在抛物线上,且OA⊥OB,过O作OP⊥AB交AB于P,求P点轨迹方程.
解:设OA=y=kx, 则![]() ,
,
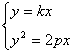 得
得![]() 同理 B(2pk2, -2pk)
同理 B(2pk2, -2pk)
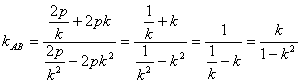
AB:![]()
![]() ....①
....①
而op: ![]() .....②
.....②
∵ P为AB与OP的交点,联立①②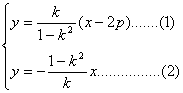 (1)×(2)消去k,
(1)×(2)消去k,
y2=-(x-2p)x, ∴ x2+y2-2px=0(x≠0)即为所求.
四、直线与圆锥曲线的位置关系
1.过点(2,4)作直线与抛物线y2=8x只有一个公共点,这样的直线有( ).
A、一条 B、两条 C、三条 D、四条
分析:首先注意点(2,4)在抛物线上,其次只有一个公共点,包括直线平行于抛物线的对称轴,与抛物线交于一点,因而选B.
2.直线y:kx+1与椭圆![]() 恒有公共点,则m的取值范围是( ).
恒有公共点,则m的取值范围是( ).
A、m≥1且m≠5 B、m≥1 C、m≠5 D、m≤5
分析:直线与椭圆恒有公共点Û联立方程Δ恒大于等于0,
由Δ≥0恒成立可得 m≥1-5k2恒成立,∴ m≥(1-5k2)max, ∴m≥1且m≠5,选A.
3.直线l: ![]() 与曲线x2-y2=1(x>0)相交于A,B两点,则直线l的倾角为(
).
与曲线x2-y2=1(x>0)相交于A,B两点,则直线l的倾角为(
).
A、[0,![]() ) B、
) B、![]() C、
C、![]() D、
D、![]()
分析:直线与双曲线右支交于两点,不能仅仅用Δ判定,
x2-k2(x2-![]() x+2)=1 (1-k2)x2+
x+2)=1 (1-k2)x2+![]() k2x-2k2-1=0
k2x-2k2-1=0
∴ 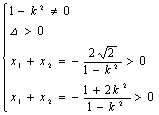 ∴ k>1 或 k<-1. ∴ 倾角
∴ k>1 或 k<-1. ∴ 倾角![]() ,选B.
,选B.
4.在抛物线y2=4x上恒有两点关于y=kx+3对称,求k范围.
解:设B、C关于直线y=kx+3对称,则BC方程为x=-ky+m,代入 y2=4x 得 y2+4ky-4m=0 设B(x, y), C(x2,
y2), BC中点M(x0, y0), ∴ ![]() , x0=2k2+m,∵ M(x0, y0)在l上,∴
-2k=k(2k2+m)+3
∴
, x0=2k2+m,∵ M(x0, y0)在l上,∴
-2k=k(2k2+m)+3
∴ ![]() , 又BC与抛物线交于两点,∴Δ=16k2+16m>0, 即
, 又BC与抛物线交于两点,∴Δ=16k2+16m>0, 即![]() ,
,![]() 解得-1<k<0.
解得-1<k<0.