高中数学第5册全册测试
说明:时间120分钟,满分150分;可以使用计算器.
一、选择题(每小题只有一个正确选项;每小题5分,共60分)
1.数列1,3,6,10,…的一个通项公式是
(A)an=n2-(n-1) (B)an=n2-1 (C)an=![]() (D)an=
(D)an=![]()
2.已知数列![]() ,3,
,3,![]() ,…,
,…,![]() ,那么9是数列的
,那么9是数列的
(A)第12项 (B)第13项 (C)第14项 (D)第15项
3.在数列{an}中,a1=1,当n≥2时,n2=a1a2…an恒成立,则a3+a5等于
(A)![]()
4.一个三角形的两内角分别为45°和60°,如果45°角所对的边长是6,那么60°角所对的边长为
(A)3![]() (B)3
(B)3![]() (C)3
(C)3![]() (D)
2
(D)
2![]()
5.在△ABC中,若∠A∶∠B∶∠C=1∶2∶3,则a∶b∶c等于
(A)1∶2∶3 (B)3∶2∶1 (C)2∶![]() ∶1 (D)1∶
∶1 (D)1∶![]() ∶2
∶2
6.在△ABC中,∠A=60°,a=![]() ,b=4,满足条件的△ABC
,b=4,满足条件的△ABC
(A)无解 (B)有解 (C)有两解 (D)不能确定
7、等差数列{![]() }的前
}的前![]() 项和记为
项和记为![]() ,若
,若![]() 为一个确定的常数,则下列各数中可以用这个常数表示的是
为一个确定的常数,则下列各数中可以用这个常数表示的是![]()
(A) ![]() (B)
(B) ![]() (C)
(C)![]() (D)
(D) ![]()
8.在等差数列{an}中,若a4+a6+a8+a10+a12=120,则2 a10-a12的值为
(A)20 (B)22 (C)24 (D)28
9. 当a<0时,不等式42x2+ax-a2<0的解集为
(A){x-![]() <x<
<x<![]() } (B){x
} (B){x![]() <x<-
<x<-![]() } (C){x
} (C){x![]() <x<-
<x<-![]() } (D){x-
} (D){x-![]() <x<
<x<![]() }
}
10.在![]() 中,
中,![]() 为三个内角,若
为三个内角,若![]() ,则
,则![]() 是 ( )
是 ( )
(A)直角三角形 (B)钝角三角形
(C)锐角三角形 (D)是钝角三角形或锐角三角形
11.已知等差数列{an}满足![]() =28,则其前10项之和为
( )
=28,则其前10项之和为
( )
(A)140 (B)280 (C)168 (D)56
12.不等式组 ![]() 表示的平面区域是 ( )
表示的平面区域是 ( )
(A ) 矩形 ( B) 三角形 (C ) 直角梯形 (D ) 等腰梯形
二、填空题(把答案写在题中的横线上;每小题4分,共16分)
13. 数列{an}中,已知an=(-1)n·n+a(a为常数)且a1+a4=3a2,则a=_________,a100=_________.
14.在△ABC中,若
![]() ___________.
___________.
15.若不等式ax2+bx+2>0的解集为{x-![]() },则a+b=_________.
},则a+b=_________.
16.黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案:
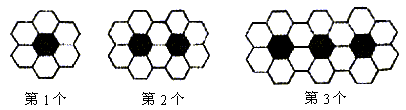
则第n个图案中有白色地面砖 块.
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分) 非等边三角形ABC的外接圆半径为2,最长的边![]() ,求
,求![]() 的取值范围.
的取值范围.
18. (本小题满分12分)在湖的两岸A、B间建一座观赏桥,由于条件限制,无法直接度量A、B两点间的距离.请你用学过的数学知识按以下要求设计一测量方案.
(1)画出测量图案;
(2)写出测量步骤(测量数据用字母表示);
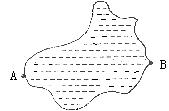 |
(3)计算AB的距离(写出求解或推理过程,结果用字母表示).
19.(本小题满分12分)设![]() 为等差数列,
为等差数列,![]() 为等比数列,
为等比数列,![]() 分别求出
分别求出![]() 及
及![]() 的前10项的和
的前10项的和![]() .
.
20.(本小题满分12分)
已知![]() ,解关于
,解关于![]() 的不等式
的不等式![]() .
.
21、(本小题满分12分)东海水晶制品厂去年的年产量为10万件,每件水晶产品的销售价格为100元,固定成本为80元.从今年起,工厂投入100万元科技成本,并计划以后每年比上一年多投入100万元科技成本.预计产量每年递增1万件,每件水晶产品的固定成本![]() 与科技成本的投入次数
与科技成本的投入次数![]() 的关系是
的关系是![]() =
=![]() .若水晶产品的销售价格不变,第
.若水晶产品的销售价格不变,第![]() 次投入后的年利润为
次投入后的年利润为![]() 万元.①求出
万元.①求出![]() 的表达式;②问从今年算起第几年利润最高?最高利润为多少万元?
的表达式;②问从今年算起第几年利润最高?最高利润为多少万元?
22.(本小题满分14分)已知等比数列![]() 的通项公式为
的通项公式为![]() ,设数列
,设数列![]() 满足对任意自然数
满足对任意自然数![]() 都有
都有![]() +
+![]() +
+![]() +┅+
+┅+![]() =
=![]() +1恒成立.
+1恒成立.
①求数列![]() 的通项公式;
的通项公式;
②求![]() ┅+
┅+![]() 的值.
的值.
参考答案:
一、选择题CCBAD ABCBB AD
二、填空题
13.-3,97;14.100![]() ;15.-14;16.
;15.-14;16.![]() .
.
三、解答题
17. 解:由正弦定理 ![]() ,得
,得![]() .
.
∵BC是最长边,且三角形为非等边三角形,
∴![]() .
.
![]()
![]()
![]() .
.
又![]() ,∴
,∴![]() ,
,
∴![]() .
.
故 ![]() 的取值范围为
的取值范围为![]()
18.略.
19.解:设等差数列![]() 的公差为
的公差为![]() 等比数列
等比数列![]() 的公比为
的公比为![]() .
.
![]() ①
①
又![]()
![]() ②
②
则由①,②得![]() -
-
![]()
将![]() 代入①,得
代入①,得![]()
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
20. 解:原不等式可化为:[x(m-1)+3](x-3)>0
![]() 0<m<1, ∴-1<
0<m<1, ∴-1<![]() -1<0, ∴
-1<0, ∴ ![]() ;
;
∴
不等式的解集是![]() .
.
21.解:第n次投入后,产量为10+n万件,价格为100元,固定成本为![]() 元,科技成本投入为100n,所以,年利润为
元,科技成本投入为100n,所以,年利润为
![]() (
(![]() )
)
=![]()
![]() (万元)
(万元)
当且仅当![]() 时,
时,
即 ![]() 时,利润最高,最高利润为520万元.
时,利润最高,最高利润为520万元.
22. 解:(1)![]() 对任意正整数n,有
对任意正整数n,有![]()
![]() +
+![]() +
+![]() +┅+
+┅+![]() =
=![]() +1 ①
+1 ①
∴当n=1时,![]() ,又
,又![]() ,∴
,∴![]() ;
;
当![]() 时,
时,![]() +
+![]() +
+![]() +┅+
+┅+![]() =
=![]() -1
②
-1
②
∴②-①得 ![]() ;
; ![]() ;
;
∴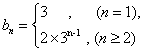
(2)![]() ┅+
┅+![]()
=![]()
=![]() =
=![]()