高三综合测试(一)
一、选择题:(5’×10)
1、当x![]() R,下列四个集合中是空集的是( )
R,下列四个集合中是空集的是( )
A. {xx2-3x+2=0} B. {xx2<x}
C. {xx2-2x+3=0}
C. {xsinx+cosx=![]() }
}
2、若命题“p或q”是真命题,“p且q”是假命题,则( )
A.命题p和命题q都是假命题 B.命题p和命题q都是真命题
C.命题p和命题“非q”的真值不同 D. 命题p和命题q的真值不同
3、函数y=2x3-3x2-12x+5在区间[0,3]上最大值与最小值分别是( )
A. 5,-15 B. 5,-4 C. -4,-15 D. 5,-16
4、设M,P是两个非空集合,定义M与P的差集为M-P={xx![]() M且x
M且x![]() p},则M-(M-P)等于( )
p},则M-(M-P)等于( )
A. P B.
M![]() P
C. M
P
C. M![]() P D. M
P D. M
5、函数f(x)在定义域R上不是常数函数,且f(x)满足条件,对任意x![]() R,都有f(4+x)=
f(4-x),f(x+1)=f(x-1),则f(x)是( )
R,都有f(4+x)=
f(4-x),f(x+1)=f(x-1),则f(x)是( )
A、奇函数但非偶函数 B、偶函数但非奇函数
C、奇函数又是偶函数 D、非奇非偶函数
6、集合A={1,2,3,4,5,6},从集合A中任选3个不同的元素组成等差数列,这样的等差数列共有( )
A、4个 B、8个 C、10个 D、12个
7、若![]() 的展开式中第三项系数等于6,则n等于( )
的展开式中第三项系数等于6,则n等于( )
A. 4 B. 8 C. 12 D. 16
8、若(1+mx)6=a0+a1x+a2x2+…+a6x6且a1+a2+…+a6=63,则实数m的值为( )
A. 1 B. -1 C. -3 D. 1或-3
9、一射手对同一目标独立地射击四次,已知至少命中一次的概率为![]() ,则此射手每次射击命中的概率为( )
,则此射手每次射击命中的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10、如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量是( )
A、19 B、20 C、24 D、26
二、填空题(5’×6)
11、满足![]()
![]()
![]() 和集合A的个数是_______个。
和集合A的个数是_______个。
12、已知函数![]() 的反函数是
的反函数是![]() 且
且![]() =______________
=______________
13、与不共面的四点距离都相等的平面共有______个。
14、已知线段AB在平面![]() 外,AB两点到平面
外,AB两点到平面![]() 的距离分别是1和3,则线段AB中点到平面
的距离分别是1和3,则线段AB中点到平面![]() 的距离是__________.
的距离是__________.
15、已知数列![]() 的通项公式为
的通项公式为![]() …
…![]() _________。
_________。
16、6位身高不同的同学拍照,要求分成两排,每排3人,则后排每人均比其前排的同学身材要高的概率是_________。
三、解答题(14’×5)
17、关于实数![]() 的不等式
的不等式![]() 的解集依次为
的解集依次为![]() 与
与![]() ,求使
,求使![]() 的
的![]() 的取值范围。
的取值范围。
18、已知函数![]()
(1)求反函数![]()
(2)判断![]() 是奇函数还是偶函数并证明。
是奇函数还是偶函数并证明。
19、由0,1,2,3,4,5这六个数字。
(1)能组成多少个无重复数字的四位数?
(2)能组成多少个无重复数字的四位偶数?
(3)能组成多少个无重复数字且被25个整除的四位数?
(4)组成无重复数字的四位数中比4032大的数有多少个?
20、如图在三棱锥S![]() 中
中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 。
。
(1)证明![]() 。
。
(2)求侧面![]() 与底面
与底面![]() 所成二面角的大小。
所成二面角的大小。
(3)求异面直线SC与AB所成角的大小。
21、已知![]() 上是减函数,且
上是减函数,且![]() 。
。
(1)求![]() 的值,并求出
的值,并求出![]() 和
和![]() 的取值范围。
的取值范围。
(2)求证![]() 。
。
(3)求![]() 的取值范围,并写出当
的取值范围,并写出当![]() 取最小值时的
取最小值时的![]() 的解析式。
的解析式。
高三数学答案
一、选择题。
| 题好 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | D | A | B | B | D | C | D | B | A |
二、填空题。
11、_____7___ 12、__2____ 13、___7____
14、__1或2___
15、![]() 16、
16、![]()
17、由
![]()
![]()
![]() ··························4分
··························4分
由![]() 得
得
![]()
当![]()
![]() 时得
时得![]()
当![]()
![]()
![]() ·························7分
·························7分
综上解述:当![]() 时若
时若![]() 则
则
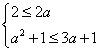
解得![]() ···················································10分
···················································10分
当![]() 时若
时若![]() 则
则
![]()
解得![]()
![]() 的范围是
的范围是![]() 或
或![]() ························14分
························14分
18、(1)令![]() 则
则![]()
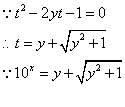
∴![]() ························7分
························7分
(2)![]()
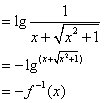
![]() 为奇函数·······················14分
为奇函数·······················14分
19、(1)![]() ·················3分
·················3分
(2)![]() ··············6分
··············6分
(3)![]() ··············9分
··············9分
(4)![]() ··············12分
··············12分
20、(1)∵∠SAB=∠SCA=900

·························································5分
(2)![]()

·················································10分
(3)![]()

![]() ····················15分
····················15分
21、(1)![]()
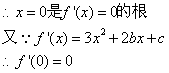
![]() ··············································2分
··············································2分

![]() ·············································5分
·············································5分
(2)![]()
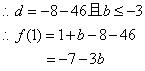
![]() ··········································10分
··········································10分
(3)![]()
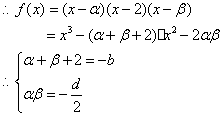
·······················································12分

![]() ··································15分
··································15分