高三综合测试(五)
一、选择题(共12小题,每小题5分)
1.已知集合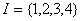 ,
, 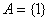 ,
,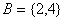 , 则A
, 则A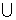 (
(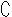 I B)=
( )
I B)=
( )
A.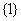 B.
B.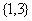 C.
C. 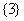 D.
D.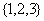
2.已知数列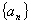 的前n项和为
的前n项和为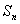 ,且
,且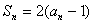 , 则
, 则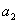 等于
( )
等于
( )
A.4 B.2 C.1 D. -2
3.不等式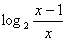 ≥1的解集为
( )
≥1的解集为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.在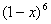 展开式中,含
展开式中,含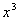 项的系数是
( )
项的系数是
( )
A.20 B. -20 C. -120 D.120
5.设α,β,γ为不同的平面,m,n,l为不同的直线,则m⊥β的一个充分条件是 ( )
A.α⊥β,α∩β=l,m⊥l B.α∩γ=m,α⊥γ,β⊥γ
C.α⊥γ,β⊥γ, m⊥α D.n⊥α,n⊥β, m⊥α
6.将直线l: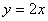 按a = (3, 0)平移得到直线
按a = (3, 0)平移得到直线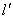 ,则
,则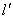 的方程为 ( )
的方程为 ( )
A.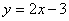 B.
B.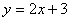 C.
C.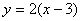 D.
D.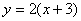
7.一个与球心距离为1的平面截球体所得的圆面面积为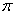 ,则球的体积为 (
)
,则球的体积为 (
)
A. 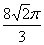 B.
B.
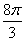 C.
C.
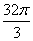 D.
8
D.
8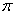
8.在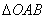 中,
中,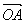 =a,
=a,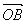 =b,M为OB的中点,N为AB的中点,ON,AM交于点P,
=b,M为OB的中点,N为AB的中点,ON,AM交于点P,
则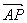 =
( )
=
( )
A.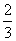 a-
a-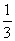 b B.-
b B.-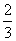 a+
a+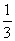 b C.
b C.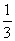 a-
a-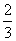 b D.-
b D.-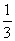 a+
a+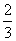 b
b
9.已知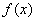 是定义在R上的函数,且
是定义在R上的函数,且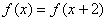 恒成立,当
恒成立,当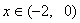 时,
时,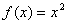 ,则当
,则当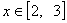 时,函数
时,函数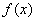 的解析式为
( )
的解析式为
( )
A.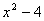 B.
B.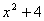 C.
C.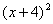 D.
D.
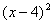
10.设F1,F2是椭圆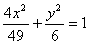 的两个焦点,P是椭圆上的点,且
的两个焦点,P是椭圆上的点,且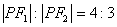 ,则
,则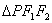 的面积为
( )
的面积为
( )
A.4 B.6
C.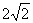 D.
D.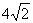
11.口袋里放有大小相等的两个红球和一个白球,有放回地每次摸取一个球,数列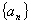 满足:
满足: 如果
如果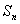 为数列
为数列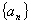 的前n项和,那么
的前n项和,那么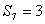 的概率为
的概率为
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.已知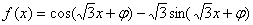 为偶函数,则
为偶函数,则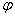 可以取的一个值为( )
可以取的一个值为( )
A.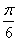 B.
B.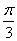 C.
C.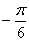 D.
D.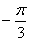
二、填空题:本大题共四小题,每小题4分,共16分,把答案填在题中横线上.
13.已知函数![]() ,则
,则 ![]() =
=
14.设x,y满足约束条件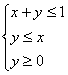 ,则
,则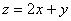 的最大值是 _________.
的最大值是 _________.
15.在数列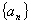 和
和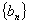 中,
中,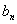 是
是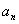 与
与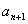 的等差中项,
的等差中项,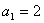 且对任意
且对任意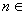 N*都有
N*都有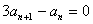 ,则数列
,则数列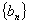 的通项公式为 ___ _______.
的通项公式为 ___ _______.
16.规定记号“⊙”表示一种运算,定义a⊙b=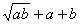 (a , b为正实数),若1⊙k<3,
(a , b为正实数),若1⊙k<3,
则k的取值范围为_________.
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
已知函数![]() .
.
(Ⅰ)求![]() 的最大值,并求出此时x的值;
的最大值,并求出此时x的值;
(Ⅱ)写出![]() 的单调递增区间.
的单调递增区间.
18.(本小题满分12分)
某公司一年需要一种计算机元件8000个,每天需同样多的元件用于组装整机,该元件每年分n次进货,每次购买元件的数量均为x,购一次货需手续费500元.已购进而未使用的元件要付库存费,假设平均库存量为![]() 件,每个元件的库存费为每年2元,如果不计其他费用,请你帮公司计算,每年进货几次花费最小?
件,每个元件的库存费为每年2元,如果不计其他费用,请你帮公司计算,每年进货几次花费最小?
19.(本小题满分12分)
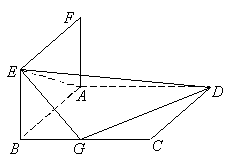
如图, 正方形ABCD和ABEF的边长均为1,且它们所在的平面互相垂直,G为BC的中点.
(Ⅰ)求点G到平面ADE的距离;
(Ⅱ)求二面角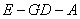 的正切值.
的正切值.
20.(本小题满分12分)
已知![]() (m为常数,且m>0)有极大值
(m为常数,且m>0)有极大值![]() ,
,
(Ⅰ)求m的值;
(Ⅱ)求曲线![]() 的斜率为2的切线方程.
的斜率为2的切线方程.
21.(本小题满分12分)
已知以向量v=(1,
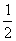 )为方向向量的直线l过点(0,
)为方向向量的直线l过点(0, 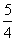 ),抛物线C:
),抛物线C: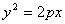 (p>0)的顶点关于直线l的对称点在该抛物线上.
(p>0)的顶点关于直线l的对称点在该抛物线上.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设A、B是抛物线C上两个动点,过A作平行于x轴的直线m,直线OB与直线m交于点N,若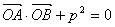 (O为原点,A、B异于原点),试求点N的轨迹方程.
(O为原点,A、B异于原点),试求点N的轨迹方程.
22.(本小题满分14分)
已知函数![]() (x≥4)的反函数为
(x≥4)的反函数为![]() ,数列
,数列![]() 满足:a1=1,
满足:a1=1,![]() ,(
,(![]() N*),数列
N*),数列![]() ,
,![]() ,
,![]() ,…,
,…,![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列.
的等比数列.
(Ⅰ)求证:数列![]() 为等差数列;
为等差数列;
(Ⅱ)若![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
数学参考答案
一、选择题: BACBD CABDB BD
二、填空题: 13.![]() 14. 2 15.
14. 2 15. ![]() 16.0<k<1
16.0<k<1
三、解答题:
17.(本小题满分12分)
(Ⅰ)![]()
![]()
![]()
![]() ………………………(6分)
………………………(6分)
当![]() ,即
,即![]()
![]() 时,
时,
![]() 取得最大值
取得最大值![]() .
……………………(8分)
.
……………………(8分)
(Ⅱ)当![]() ,即
,即![]()
![]() 时,
时,
所以函数![]() 的单调递增区间是
的单调递增区间是![]()
![]() .………(12分)
.………(12分)
18.(本小题满分12分)
设购进8000个元件的总费用为S,一年总库存费用为E,手续费为H.
则![]() ,
,![]() ,
,![]() ……………(3分)
……………(3分)
所以S=E+H=![]() ………………………(6分)
………………………(6分)
=![]() ………………………(8分)
………………………(8分)
=![]() ………………………(10分)
………………………(10分)
当且仅当![]() ,即n=4时总费用最少,故以每年进货4次为宜.………(12分)
,即n=4时总费用最少,故以每年进货4次为宜.………(12分)
19.(本小题满分12分)
(Ⅰ)∵BC∥AD, AD![]() 面ADE,
面ADE,
∴点G到平面ADE的距离即点B到平面ADE的距离.
连BF交AE于H,则BF⊥AE,又BF⊥AD.
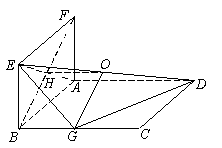 ∴BH即点B到平面ADE的距离.………………………(2分)
∴BH即点B到平面ADE的距离.………………………(2分)
在Rt△ABE中,![]() .
.
∴点G到平面ADE的距离为![]() .…(4分)
.…(4分)
(Ⅱ)过点B作BN⊥DG于点N,连EN,
由三垂线定理知EN⊥DN. ………………………(6分)
∴![]() 为二面角
为二面角![]() 的平面角.………………………(8分)
的平面角.………………………(8分)
在Rt△BNG中,![]()
∴![]()
则Rt△EBN中,![]() ………………………(10分)
………………………(10分)
所以二面角![]() 的正切值为
的正切值为![]() . ………………………(12分)
. ………………………(12分)
20.(本小题满分12分)
(Ⅰ)![]()
![]() …………(2分)
…………(2分)
则![]() ,
,![]() ………………………………………………(4分)
………………………………………………(4分)
由列表得:
| x |
| -m |
|
|
|
|
| + | 0 | - | 0 | + |
|
|
| 极大值 |
| 极小值 |
|
![]()
![]() ,∴
,∴![]() . …………(6分)
. …………(6分)
(Ⅱ)由(Ⅰ)知![]() ,则
,则![]()
∴![]() 或
或![]() …………………………………………(8分)
…………………………………………(8分)
由![]() ,
,![]() .
.
所以切线方程为:![]() 即
即![]() ; ………(10分)
; ………(10分)
或![]() 即
即![]() ……………………(12分)
……………………(12分)
21.(本小题满分12分)
(Ⅰ)由题意可得直线l:![]() ①
①
过原点垂直于l的直线方程为 ![]() ②
②
解①②得![]() . …………………………………………(3分)
. …………………………………………(3分)
∵抛物线的顶点关于直线l的对称点在该抛物线的准线上.
∴![]() ,
,![]()
∴抛物线C的方程为![]() .
………………………(6分)
.
………………………(6分)
(Ⅱ)设![]() ,
,![]() ,
,![]() ,
,
由![]() ,得
,得![]() .
.
又![]() ,
,![]() .
.
解得 ![]() ③ ………………………(8分)
③ ………………………(8分)
直线ON:![]() ,即
,即![]() ④ ……………(10分)
④ ……………(10分)
由③、④及![]() 得,
得,
点N的轨迹方程为![]()
![]() .………………………(12分)
.………………………(12分)
22.(本小题满分14分)
(Ⅰ)∵![]()
![]() (x≥4),
(x≥4),
∴![]()
![]() (x≥0), ……………………………………(2分)
(x≥0), ……………………………………(2分)
∴![]()
![]() ,
,
即![]() (
(![]() N*). ……………………………(4分)
N*). ……………………………(4分)
∴数列![]() 是以
是以![]() 为首项,公差为2的等差数列.……………(6分)
为首项,公差为2的等差数列.……………(6分)
(Ⅱ)由(Ⅰ)得:![]() ,即
,即
![]() (
(![]() N*). ……………………………(8分)
N*). ……………………………(8分)
b1=1,当n≥2时,![]() ,
,
∴![]()
![]()
![]()
因而![]() ,
,![]() N*. ……………………………(10分)
N*. ……………………………(10分)
![]()
![]() ,
,
∴![]()
![]()
![]()
令![]()
![]() ①
①
则![]()
![]() ②
②
①-②,得
![]()
![]()
![]()
∴![]() .又
.又![]() .
.
∴![]() . ……………………………(14分)
. ……………………………(14分)