高三数学选用试题
一、选择题:
1.不等式![]() 的解集是
( D
)
的解集是
( D
)
A.(-1,3)
B.(-3,1)![]() (3,7)
(3,7)
C.(-7,-3)
D.(-7,-3)![]() (-1,3)
(-1,3)
2.已知a是非0实数,则“a>1”是“![]() ”的
( A )
”的
( A )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.在等差数列![]() 中,若
中,若![]() ,则
,则![]() 的值为( C )
的值为( C )
A.14 B.15 C.16 D.17
4.在![]() 中,
中,![]() ,则
,则![]() 是
( C )
是
( C )
A.正三角形 B.锐角三角形 C.直角三角形 D.钝角三角形
5.函数![]() 的图象大致是
( D)
的图象大致是
( D)
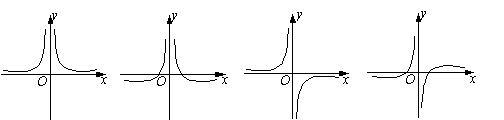
A. B. C. D.
6.已知直线a、b都在平面M外,a、b在平面M内的射影分别是直线a1、b1,给出下列四个命题:①![]() ②
②![]() ③
③![]()
④其中不正确的命题的个数是: ( D )
A.1 B.2 C.3 D.4
7.函数![]() 的定义域为[a,b],值域为
的定义域为[a,b],值域为![]() ,则b-a的最大值和最小值之和为( B)
,则b-a的最大值和最小值之和为( B)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.如果以原点为圆心的圆经过双曲线![]() 的焦点,而且被该双曲线的右准线分成的弧长为2:1的两段圆弧,那么该双曲线的离心率e等于: ( C )
的焦点,而且被该双曲线的右准线分成的弧长为2:1的两段圆弧,那么该双曲线的离心率e等于: ( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知符号函数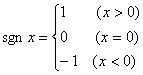 ,则方程
,则方程![]() 的所有解的和是(D )
的所有解的和是(D )
A.0
B.2 C.![]() D.
D.![]()
10.已知函数![]() 的反函数
的反函数![]() ,若
,若![]() ,则
,则![]() 的最小值为( B)
的最小值为( B)
A.1
B.![]() C.
C.![]() D.
D.![]()
11.要从10名女生与5名男生中选取6名学生组成6名课外兴趣味小组,如果按性别分层随机抽样,试问组成课外兴趣小组的概率是 ( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.实系数方程![]() 的一根大于0且小于1,另一根大于1且小于2,则
的一根大于0且小于1,另一根大于1且小于2,则![]() 的取值范围是
( A )
的取值范围是
( A )
A![]() B
B![]() C
C![]() D
D![]()
13.已知直线![]() (a,b不全为0)与圆
(a,b不全为0)与圆![]() 有公共点,且公共点的横、纵坐标均为整数,那么这样的直线共有
(B )
有公共点,且公共点的横、纵坐标均为整数,那么这样的直线共有
(B )
A.66条 B.72条 C.74条 D.78条
14.某新区新建有5个住宅小区(A、B、C、D、E),现要铺设连通各小区的自来水管道,如果它们两两之间的线路长如下表:
|
| A | B | C | D | E | ||||||||||||||
A | 5 | 7 | 8 | 5 | |||||||||||||||
| B | 3 | 5 | 2 | ||||||||||||||||
| C | 5 | 4 | |||||||||||||||||
| D | 4 | ||||||||||||||||||
| E |
请问:最短的管线长为 ( B ) A.13 B.14 C.15 D.17
15.如果一个点是一个指数函数的图象与一个对数函数的图象的公共点,那么称这个点为“好点”。在下面的五个点![]() 中,“好点”的个数为(C)
中,“好点”的个数为(C)
A.0个 B.1个 C. 2个 D.3个
16.某人的密码箱上的密码是一种五位数字号码,每位上的数字可在0到9这10个数字中选取,该人记得箱子的密码1,3,5位均为0,而忘记了2,4位上的数字,只要随意按下2,4位上的数字,则他按对2,4位上的数字的概率是 ( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
17.设命题P:函数f(x)=![]() (a>0)在区间(1,
2)上单调递增;命题Q:不等式x-1-x+2<4a对任意x∈R都成立。若“P或Q”是真命题,“P且Q”是假命题,则实数a的取值范围是
(a>0)在区间(1,
2)上单调递增;命题Q:不等式x-1-x+2<4a对任意x∈R都成立。若“P或Q”是真命题,“P且Q”是假命题,则实数a的取值范围是
(C)
A.![]() <a≤1
B。
<a≤1
B。![]() ≤a<1
C.0<a≤
≤a<1
C.0<a≤![]() 或a>1 D。0<a<
或a>1 D。0<a<![]() 或a≥1
或a≥1
二、填空题
18.设二项式![]() 的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n等于
4
的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n等于
4
19.半径为2的球内接四面体A-BCD,AB、AC、AD两两互相垂直,则![]() +
+![]() +
+![]() 的最大值为 8 。
的最大值为 8 。
20.雅典奥运会的第三天共产生8枚金牌,分别为中国4枚,美国2枚,日本、希腊各一枚,在奏国歌的先后顺序中,奏希腊国歌的前后都是奏中国国歌,美国国歌不连在一起奏的,则这天奏国歌的不同顺序____120____种
21.已知函数f(x)=Acos2(ωx+![]() )(A>0,ω>0)的最大值为3,f(x)的图象在y轴上的截距为2,其相邻两对称轴间的距离为2,则f(1)+f(2)+f(3)+…+f(100)=____ 100 ______
)(A>0,ω>0)的最大值为3,f(x)的图象在y轴上的截距为2,其相邻两对称轴间的距离为2,则f(1)+f(2)+f(3)+…+f(100)=____ 100 ______
22.A、B两点之间有5条网线并联,它们能通过的最大信息量分别为1,1,2,3,4,现从中任取三条网线且使这三条网线通过最大信息量的和大于等于7的方法共有 5
23.对任意两实数a、b、,定义运算“*”如下:
![]() 的值域为
的值域为![]()
24.已知函数![]() ,若
,若![]() 的单调减区间是 (0,4),则在曲线
的单调减区间是 (0,4),则在曲线![]() 的切线中,斜率最小的切线方程是
的切线中,斜率最小的切线方程是 ![]() 。
。
25.有一组数据:![]()
![]() 的算术平均值为10,若去掉其中最大的一个,余下数据的算术平均值为9;若去掉其中最小的一个,余下数据的算术平均值为11,第一个数
的算术平均值为10,若去掉其中最大的一个,余下数据的算术平均值为9;若去掉其中最小的一个,余下数据的算术平均值为11,第一个数![]() 关于
关于![]() 的表达式是
的表达式是![]() ,第
,第![]() 个数
个数![]() 关于
关于![]() 的表达式是
的表达式是![]() 。
。
 26.如下图,它满足:
26.如下图,它满足:
(1) 第n行首尾两数均为n ;
(2)表中的递推关系类似杨辉三角.
则第n行(n≥2)第2个数是![]() 。
。
三、解答题
27. 若![]() 中,a,b,c分别是
中,a,b,c分别是![]() 的对边,且
的对边,且![]() ,
,
(1)
求![]() ;
;
(2)
若![]() ,
,![]() 的面积为
的面积为![]() ,求b+c的值。
,求b+c的值。
解:(1)由![]() 得:
得:![]() ,
,
可得:![]() ,
,![]() ,
,![]() 。
。
(2)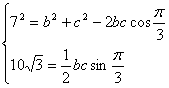
![]() ,
,![]() 。
。
28.已知![]()
且![]() (1)求
(1)求![]() ; (2)求
; (2)求![]()
解:(1)由![]()
![]()
![]()
![]()
(2)由![]()
则![]()
由![]()
在![]() 时,
时,
![]() 矛盾,故舍去.
矛盾,故舍去.
在![]() 可取. 因此
可取. 因此![]()
29. 某人抛掷一枚硬币,出现正反的概率都是![]() ,构造数列
,构造数列![]() ,使得
,使得 ,记
,记![]() 。
。
(1)
求![]() 的概率;
的概率;
(2)
若前两次均出现正面,求![]() 的概率。
的概率。
解:(1)![]() ,需4次中有3次正面1次反面,设其概率为
,需4次中有3次正面1次反面,设其概率为![]()
则![]()
(2)6次中前两次均出现正面,要使![]() ,则后4次中有2次正面、2次反面或3次正面、1次反面。设其概率为
,则后4次中有2次正面、2次反面或3次正面、1次反面。设其概率为![]() 。
。
![]()
30.某食品厂定期购买面粉,已知该厂每天需要面粉6吨,每吨面粉的价格为1800元,面粉的保管与其费用为平均每天3元,购买面粉每次支付运费900元。
(1) 求该厂多少购买一次面粉才能使平均每天支付的总费用最小;
(2) 若提供面粉的公司规定,当一次购买面粉不少210吨时其价格可享受九折惠(即原价的90%)。问该厂是否考虑利用此优惠条件,请说明理由。
解(1)设该厂应隔x天购买一次面粉,其购买量为6x吨,则面粉的保管与其它费用
![]() ,平均每天支出的费用为
,平均每天支出的费用为![]() ,则
,则
![]()
![]()
![]()
![]()
![]()
即每隔10天购买一次才能使平均每天支付的总费用最小。
(2)若厂家利用此优惠条件,则至少35天购买一次面粉,设该厂利用此优惠条件,每隔x天(x![]() ) 购买一次面粉,平均每天支出的费用为
) 购买一次面粉,平均每天支出的费用为![]() 。
。
![]()
利用单调性可证![]()
![]() 在
在![]() 上递增。
上递增。
![]() 时
时![]() 取得最小值,即
取得最小值,即![]() ,
,
![]() 该厂应接受此优惠条件。
该厂应接受此优惠条件。
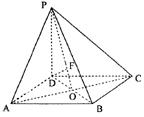
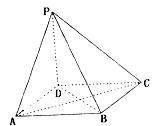 31.已知ABCD是正方形,PD⊥平面ABCD,PD=AD=2.
31.已知ABCD是正方形,PD⊥平面ABCD,PD=AD=2.
(Ⅰ)求PC与平面PBD所成的角;
(Ⅱ)求点D到平面PAC的距离;
(Ⅲ)在线段PB上是否存在一点E,使PC⊥平面ADE?
若存在,确定E点的位置,若不存在,说明理由.
解: (Ⅰ)设AC与BD相交于点O,连接PO。
∵ABCD是正方形,∴AC⊥BD。
又∵PD⊥平面ABCD,∴PD⊥AC。
∵BD∩PD=D, ∴AC⊥平面PBD。
∴∠CPO为PC与平面PBD所成的角。
∵PD=AD=2,则OC=![]() ,PC=2
,PC=2![]() 。
。
|
∴![]()
∴PC与平面PBD所成的角为30°
(Ⅱ)过D做DF⊥PO于F,∵AC⊥平面PBD,
DF![]() 平面PBD, ∴AC⊥DF。
平面PBD, ∴AC⊥DF。
|
在Rt△PDO中,∠PDO=90°,
∴PO·DF=PD·DO。 ∴![]()
(Ⅲ)假设存在E点,使PC⊥平面ADE.
过E在平面PBC内做EM∥PC交BC于点M,
连接AE、AM.
由AD⊥平面PDC可得AD⊥PC. ∵PC∥EM,∴AD⊥EM.
要使PC⊥平面ADE,即使EM⊥平面ADE. 即使EM⊥AE.
设BM=![]() ,则EM=
,则EM=![]() ,EB=
,EB=![]() . 在△AEB中由余弦定理得AE2=4+3
. 在△AEB中由余弦定理得AE2=4+3![]() -4
-4![]()
在Rt△ABM中,∠ABM=90°. ∴AM2=4+![]() .
.
∵EM⊥AE,∴4+![]() =4+3
=4+3![]() -4
-4![]() +2
+2![]() . ∴
. ∴![]() -
-![]() =0. ∵
=0. ∵![]() ,∴
,∴![]() =1.
=1.
∴E为PB的中点,即E为PB的中点时,PC⊥平面ADE.
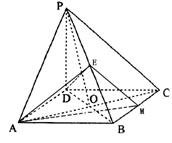
 32.如图,平面PAD
32.如图,平面PAD![]() 平面ABCD,
平面ABCD,![]() PAD是正三角形,
PAD是正三角形,
ABCD是矩形,M是AB的中点,PC与平面ABCD成![]() 角。
角。
(1)
求![]() 的值;
的值;
(2) 求二面角P-MC-D的大小;
(3) 当AD的长为多少时,点D到平面PMC的距离为2。
解:(1)取AD中点H,则![]() ,
,![]() 面PAD
面PAD![]() 平面ABCD,
平面ABCD,
![]() 面ABCD,
面ABCD,![]() PC与面ABCD所成的角为
PC与面ABCD所成的角为![]() 。
。
设AD=a,则![]() ,
,![]() ,
,![]()
![]()
![]() 。
。
(2)连结HM,由![]() ∽
∽![]() 可得:
可得:![]() 。
。

![]() ,由三垂线定理得
,由三垂线定理得![]() ,
,
![]()
![]() 是二面角P-MC-D的平面角。
是二面角P-MC-D的平面角。
![]() ,
,![]() 。
。
二面角P-MC-D的平面角为![]()
由![]() 可得:AD=
可得:AD=![]() 。
。
33.曲线![]() 有极小值,当
有极小值,当![]() 处有极大值,且在x=1处切线的斜率为
处有极大值,且在x=1处切线的斜率为![]() .
.
(1)求![]() ;
;
(2)曲线上是否存在一点P,使得y=![]() 的图象关于点P中心对称?若存在,请求出点P坐标,并给出证明;若不存在,请说明理由.
的图象关于点P中心对称?若存在,请求出点P坐标,并给出证明;若不存在,请说明理由.
解:f′(x)=3ax2+2bx+c ∵当x=1±![]() 时 f(x)有极小值及极大值
时 f(x)有极小值及极大值
∴f′(1±![]() )=0 即1±
)=0 即1±![]() 为3ax2+2bx+c=0两根
为3ax2+2bx+c=0两根
![]()
∴b=-3a , c=-6a
又∵f(x)在x=1处切线的斜率为![]()
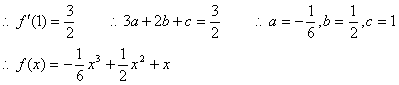
(2)假设存在P(x0, y0),使得f(x)的图象关于P中心对称,
则f(x0+x)+f(x0-x)=2y0
即-![]() (x0+x)3+
(x0+x)3+![]() (x0+x)2+x0+x-
(x0+x)2+x0+x-![]() (x0-x)3+
(x0-x)3+![]() (x0-x)2+x0-x=2y0
(x0-x)2+x0-x=2y0
化解得![]()
∵对于任意x∈R等式都成立
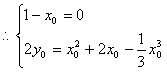
∴x0=1, y0=![]() .易知P(1,
.易知P(1,![]() )在曲线y=f(x)上.
)在曲线y=f(x)上.
∴曲线上存在P(1,![]() )使得f(x)的图象关于中心对称
)使得f(x)的图象关于中心对称
34.已知函数![]() ,且函数
,且函数![]() 的图像关于原点对称,其图像在x=3处的切线方程为8x-y-18=0。
的图像关于原点对称,其图像在x=3处的切线方程为8x-y-18=0。
(1)
求![]() 的解析式;
的解析式;
(2)
是否存在区间[a,b],使得函数g(x)的定义域和值域均为[a,b],且解析式与![]() 的解析式相同?若存在,求出这样的一个区间[a,b];若不存在,请说明理由。
的解析式相同?若存在,求出这样的一个区间[a,b];若不存在,请说明理由。
解:(1)![]()
![]() 的图像关于原点对称,
的图像关于原点对称,![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,![]() 。
。![]() ,
,![]()
又![]() 的图像在x=3处的切线方程为
的图像在x=3处的切线方程为![]() ,
,
即![]() ,据题意得:
,据题意得:![]() 解得:
解得: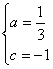 ,
,
![]()
(2)由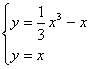 得x=0或
得x=0或![]() 。
。
又![]() ,由
,由![]() 得
得![]() ,且当
,且当![]() 或
或![]() 时,
时,![]() ,当
,当![]() 时
时![]() 。
。
所以,函数![]() 在
在![]() 和
和![]() 上递增,在
上递增,在![]() 上递减。
上递减。
于是,函数在![]() 上的极大值和极小值分别为
上的极大值和极小值分别为
![]() ,
,![]() 而
而![]() ,
,
故存在这样的区间[a,b],其中满足条件的一个区间![]()
35.已知一次函数f(x)的图像关于直线x-y=0对称的图像为C,且f(-1)=0,若点(n+1,![]() 在曲线C上,并有
在曲线C上,并有![]() 。
。
(1) 求曲线C的方程;
(2)
求数列![]() 的通项公式;
的通项公式;
(3)
设![]() ,若
,若![]() 恒成立,求实数M的取值范围。
恒成立,求实数M的取值范围。
解:(1)设f(x)=kx+b(k![]() 0),则曲线C的方程为
0),则曲线C的方程为![]() 。
。
![]() f(-1)=0,
f(-1)=0,![]() -k+b=0
①
-k+b=0
①
又点(n+1,![]() 在曲线C上,
在曲线C上,![]() 即(2,1)在曲线上。
即(2,1)在曲线上。
![]() ②
由①②得:k=b=1
②
由①②得:k=b=1
![]() C:x-y-1=0。
C:x-y-1=0。
(2)点(n+1,![]() 在曲线C上,
在曲线C上,![]()
![]() ,而
,而![]() 。
。
![]() ,
,![]()
(3)![]() 。
。
![]() 关于n单调增。
关于n单调增。![]() 。
。
故![]() 恒成立,则
恒成立,则![]()
36.已知:![]() =(c,0)(c>0),
=(c,0)(c>0),![]() ,
,![]() 最小值为1.若动点P同时满足下列条件①
最小值为1.若动点P同时满足下列条件①![]() ②
②![]() 其中
其中![]() ③动点P的轨迹C过点B(0,-1).
③动点P的轨迹C过点B(0,-1).
(1) 求c的值;
(2) 求曲线C的方程;
(3)
过点M(0,2)的直线![]() 与曲线C的轨迹交于A,B两点,求
与曲线C的轨迹交于A,B两点,求![]() 的取值范围.
的取值范围.
解:(1) ![]() ,
,
当![]() 时,
时, ![]() 的最小值为1,
的最小值为1,![]() ,
,![]() ,
,![]() .
.
(2)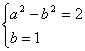 ,
,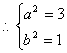 ,
, ![]() 曲线C的方程为
曲线C的方程为![]() .
.
(3)设直线![]() 的方程为:
的方程为:![]() .
.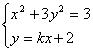
![]()
![]() (*)
(*)
由![]() 得:
得:![]()
![]()
![]()
![]()
![]() ,又
,又![]() ,
,![]()
![]() .
.
当k不存在时, ![]() =3,所以
=3,所以![]() .
.
37.如图所示,已知A,B为椭圆![]() 和双曲线
和双曲线![]() 的公共顶点。P,Q分别为双曲线和椭圆上不同于A、B的动点,且有
的公共顶点。P,Q分别为双曲线和椭圆上不同于A、B的动点,且有![]() ,设AP,BP,AQ,BQ的斜率分别为
,设AP,BP,AQ,BQ的斜率分别为![]() 。
。
(Ⅰ)求证;![]() ;
;
(Ⅱ)设![]() 分别为椭圆和双曲线的右焦点,
分别为椭圆和双曲线的右焦点,
若
PF2∥QF1 ,求![]() 的值。
的值。
解(Ⅰ):设点P,Q的坐标分别为![]()
则![]() ,即
,即![]()
所以![]()
类似地![]()
设O为原点,则![]()
∵![]() ∴
∴![]() , ∴三点O,P,Q共线
, ∴三点O,P,Q共线
∴![]() ,由①②得
,由①②得![]()
(Ⅱ)证明:因点Q在椭圆上,有![]()
由![]() 知
知![]()
即![]() ,从而
,从而![]() ……③
……③
又点P在双曲线上,有![]() …………④
…………④
由③④解得![]()
因![]() ,∴
,∴![]() ,故
,故![]()
所以![]()
由①得![]()
同理![]()
另一方面![]()
类似地![]()
所以![]()
38.对数列![]() ,规定
,规定![]() 为数列
为数列![]() 的一阶差分数列,其中
的一阶差分数列,其中![]() 。对正整数k,规定
。对正整数k,规定![]() 为
为![]() 的k阶差分数列,其中
的k阶差分数列,其中![]() 。
。
(1) 若数列![]() 首项
首项![]() ,且满足
,且满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2) 对(1)中的数列![]() ,是否存在等差数列
,是否存在等差数列![]() ,使得
,使得![]() 对一切正整数
对一切正整数![]() 都成立?若存在,求数列
都成立?若存在,求数列![]() 的通项公式;若不存在,请说明理由;
的通项公式;若不存在,请说明理由;
(3) 令![]() ,设
,设![]() ,若
,若![]() 恒成立,求最小的正整数M的值。
恒成立,求最小的正整数M的值。
解(1)![]() 而
而![]() 可得
可得![]()
![]() ,
,![]() ,
,![]()
![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,
的等差数列,
![]() ,
,![]()
(2)![]() 即:
即:![]()
而![]()
![]()
=![]() 故可得
故可得![]()
![]() 存在等差数列
存在等差数列![]() ,
,![]() 使
使![]() 对一切正整数
对一切正整数![]() 都成立。
都成立。
(3)由(2)知1![]() ……… ①
……… ①
![]() ……… ②
……… ②
①-②得:![]()
![]()
![]() ,
,![]() 递增 ,且
递增 ,且![]() 。
。
![]() 满足条件的最小的正整数M的值为6
满足条件的最小的正整数M的值为6
39.过P(1,0)做曲线![]() 的切线,切点为Q1,设Q1在
的切线,切点为Q1,设Q1在![]() 轴上的投影为P1,又过P1做曲线C的切线,切点为Q2,设Q2在
轴上的投影为P1,又过P1做曲线C的切线,切点为Q2,设Q2在![]() 轴上的投影为P2,…,依次下去得到一系列点Q1、Q2、Q3、…、Qn的横坐标为
轴上的投影为P2,…,依次下去得到一系列点Q1、Q2、Q3、…、Qn的横坐标为![]() 求证:
求证:
(Ⅰ)数列![]() 是等比数列;
是等比数列;
(Ⅱ)![]() ;
;
(Ⅲ)![]()
解:(Ⅰ)![]() 若切点是
若切点是![]() ,
,
则切线方程为![]()
当![]() 时,切线过点P(1,0)即
时,切线过点P(1,0)即![]() 得
得![]()
当![]() 时,切线过点
时,切线过点![]() 即
即![]() 得
得![]()
∴数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列. ![]() …6分
…6分
(Ⅱ)![]()
![]()
(Ⅲ)记![]() ,
,
则![]()
两式相减![]()
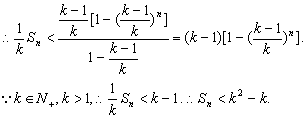
40.已知函数![]() .
.
(1)求![]() 及
及![]() 的值;
的值;
(2)是否存在自然数![]() ,使
,使![]() 对一切
对一切![]() 都成立,若存在,求出自然数
都成立,若存在,求出自然数![]() 的最小值;不存在,说明理由;
的最小值;不存在,说明理由;
(3)利用(2)的结论来比较![]() 和
和![]()
![]() 的大小.
的大小.
解(1)![]() ;
;![]() .
.
(2)假设存在自然数![]() ,使
,使![]() 对一切
对一切![]() 都成立.
都成立.
由![]() ,
,![]() 得
得 ![]() ,
,
当![]() 时,不等式
时,不等式![]() 显然不成立.
显然不成立.
当![]() 时,
时,![]() ,
,
当n=1时,显然![]() ,
,
当![]() 时,
时,![]() =
=![]() 成立,则
成立,则 ![]() 对一切
对一切![]() 都成立.
都成立.
所以存在最小自然数![]() 。
。
(3). 由![]()
![]() (
(![]() ),所以
),所以![]() ,
,![]() ,……,
,……,![]() ,
,
相乘得![]() ,∴
,∴
![]()
![]() 成立.
成立.