高考文科数学仿真测试卷
文科数学(二)
本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分。考试时间120分钟。
参考公式：
如果事件A、B互诉，那么：
如果事件A、B相互独立，那么
如果事件A在一次试验中发生的概率是P，那行n次独立重复试验中恰好发生k次的概率是：
球的表面积公式：
其中R表示球的半径.
球的体积公式：
，其中R表示球的半径.
注意事项：
1．请考生务必将自己的姓名、准考证号填写在指定地方。
2．答第Ⅰ卷时，每小题选出答案后，填在第Ⅱ卷答题卡上；答第Ⅱ卷直接在试卷指定
区域作答。
3．考试结束，监考人员将第Ⅰ卷和第Ⅱ卷一并收回。
第Ⅰ卷（选择题 共60分）
一、选择题（本大题共2小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1、若p, q∈R，则
成立的一个充分不必要条件是
A．q＞p＞0 B．p＞q＞0 C．p＜q＜0 D．p=q≠0
2、把函数y=2x−2+3的图象按向量
平移，得到函数y=2x+1−1的图象，则向量
A．(−3, −4) B．(3, 4) C．(−3, 4) D．(3, −4)
3、在ΔABC中，a=5，b=8，C=60°，则
A．20 B．−20 C．
D．
4、各项均不为零的等差数列{an}中，若
则
A．0 B．−2006 C．2006 D．4012
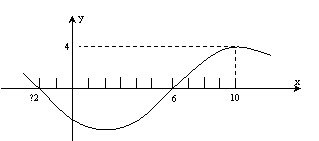
5、已知函数
的部分图象如图，则函数关系式为
A．
B．
C．
D．
6、集合P={1, 4, 9, 16…}，若a∈P,
b∈P则a
b∈P，则运算可能是
A．加法 B．减法 C．除法 D．乘法
7、在ΔABC中，
，若ΔABC的最长边为
，则最短边的长为
A．2 B．
C．
D．1
8、函数f (x)为奇函数且f (3x+1)的周期为3，f (1)=－1，则f (2006)等于
A．0 B．1 C．一1 D．2
9、已知向量a＝(2cosα，2sinα)，b＝(3cosβ，3sinβ)，a与b的夹角为60o，则直线xcosα－ysinα
＋1＝0与圆(x－cosβ)2＋(y＋sinβ)2＝1的位置关系是
A、相切 B、相交 C、相离 D、随α、β的值而定
10、有一个游戏：将分别写有数字1，2，3，4的四张卡片随机发给甲、乙、丙、丁4个人，
每人一张，并请4个人进行预测：
甲说：乙或丙拿到标有3的卡片； 乙说：甲或丙拿到标有2的卡片；
丙说：标有1的卡片在甲手中； 丁说：甲拿到标有3的卡片.
结果显示：甲、乙、丙、丁4个人预测的都不正确.那么甲、乙、丙、丁4个人拿到的卡片依次为
A. 3124 B. 4123 C. 4321 D. 4213
11．{an}为等差数列，若
，且它的前n项和Sn有最小值，那么当Sn取得最小正值时，n=
A．11 B．17 C．19 D．21
12．设对任意实数x∈[−1, 1]，不等式x2+ax−3a＜0总成立，则实数a的取值范围是
A．a＞0 B．a＞0或a＜−12 C．
D．
第Ⅱ卷（非选择题 共90分）
二、填空题（本大题共4小题，每小题4分，共16分，把答案填在横线上.）
13、在(1－)15的展开式中，系数最大的项是第 项．
14．已知函数
，若
的单调减区间是
，则在曲线
的切线中，斜率最小的切线方程是_________________.
15、已知： 命题p：不等式x－m＋x－1＞1的解集为R，
命题q：f(x)＝log(3＋m)x是(0，＋∞)上的增函数．
若“p且q”是假命题，“p或q”是真命题，则实数m的取值范围是 ．
16、下表给出了四组命题：
|
|
| |
| ① | 直线 |
|
| ② | 直线 |
|
| ③ | 平面 | 直线 |
| ④ | 平面 | 平面 |
∥平面
上两点到
，且其中满足
是
的充分必要条件的序号是_________________。
三、解答题：（本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.）
17、 (本题满分12分)
在△
中，已知a、b、
分别是三内角
、
、
所对应的边长,且
（Ⅰ）求角的大小；
（Ⅱ）若
，求角的大小.
18、(本题满分12分)
一个口袋内装有大小相同且已编有不同号码的6个黑球和4个红球，某人一次从中摸出
2个球
（I）如果摸到的球中含有红球就中奖，那么此人中奖的概率是多少？
（II）如果摸到的2个球都是红球，那么就中大奖，在有放回的3次摸球中，此人恰好两次中大奖的概率是多少？
19、已知数列{log2(an−1)} n∈N *为等差数列，且a1=3, a3=9
（I）求an （II）求证
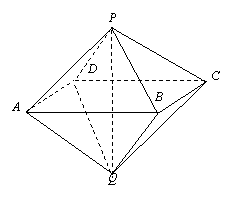
20、（本题满分12分）
如图,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2,AB=4.
⑴ 证明PQ⊥平面ABCD;
⑵ 求异面直线AQ与PB所成的角;
⑶ 求点P到平面QAD的距离.
22、(本小题满分12分)
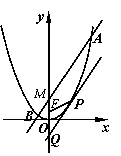如图，设抛物线C：x2=4y的焦点为F，P(x0, y0)为抛物线上的任一点（其中x0≠0），过P点的切线交y轴于Q点．
（1）证明：
；
（2）Q点关于原点O的对称点为M，过M点作平行于PQ的直线交
抛物线C于A、B两点，若
，求
的值．
21、（本小题满分14分）已知函数
的最大值为正实数，集合
，集合
。
（1）求和；
（2）定义与的差集：
且
。
设
，
，
均为整数，且
。
为取自
的概率，
为取自
的概率，写出与的二组值，使
，
。
（3）若函数
中，
，
是（2）中较大的一组，试写出在区间[
,
]上的最大值函数
的表达式。
参考答案：
一、选择题（本大题共2小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | A | B | C | A | D | D | B | C | D | C | C |
简答与提示：
1、当q＞p＞0时，
∴ 若，则q＞p＞0或0＞p＞q
2、设
，由题意有
∴
3、由题意可知
4、设公差为d，则an+1=an+d, an−1=an−d，∴
5、由图象可知函数过(−2, 0), (6, 0), T=16, 
，将函数
向右平移6个单位得到
或用排除法，令x=−2, y=0，排除B、C，令x=8，则y＞0，排除D
6、由a∈P, b∈P可设a=x2, b=y2， ∴ab=x2y2=(xy)2∈P
7、由
得
，
∴∠C的对边AB为最长边，∠B的对边AC为最短边，由正弦定理得：
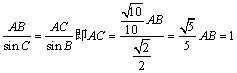
8、由已知f (3x+1)=f[3(x+3)+1]=f(3x+1+9)，所以f(x)的周期为9，
f(2006)=f(2007－1)=f(－1)=－f(1)=1.
9、a与b的夹角为60o
，
10、乙丙丁所说为假甲拿4，甲乙所说为假丙拿1，甲所说为假乙拿2；
11．∵Sn有最小值，∴d＜0则a10＞a11，又，∴a11＜0＜a10
∴a10+a11＜0，
S20=10(a1+a20)=10(a10+a11)＜0, S19=19a10＞0又a1＞a2＞…＞a10＞0＞a11＞a12＞…
∴S10＞S9＞…＞S2＞S1＞0, S10＞S11＞…＞S19＞0＞S20＞S21＞…
又∵S19−S1=a2+a3+…+a19=9(a10+a11)＜0 ∴S19为最小正值
12．由不等式x2+ax−3a＜0, x∈[−1, 1]时恒成立，可得不等式
，x∈[−1, 1]时恒成立，令
，由x∈[−1, 1]得3−x∈[2, 4]，当3−x=3即x=0时，函数f(x)有最小值0，又
二、填空题（本大题共4小题，每小题4分，共16分，把答案填在横线上.）
13、9
14、
15、
16、①②③④
简答与提示：
13、二项式系数是中间两项最大，但相应的展开式的系数一正一负
14．
，令
得
，∴当
时，斜率最小为
，
此时，切点是
，所以切线方程为；
15、命题p：不等式x－m＋x－1＞1的解集为R
或
命题q：f(x)＝log(3＋m)x是(0，＋∞)上的增函数
3＋m>1
“p且q”是假命题，“p或q”是真命题说明命题p和q一真一假，
所以实数m的取值范围是.
16、根据有关性质和判断
三、解答题：（本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.）
17、 (本题满分12分)
解：（Ⅰ）在△ABC中，
（Ⅱ）由正弦定理,又,故
即: 
故△ABC是以角C为直角的直角三角形
又
18、(本题满分12分)
解：（1）记“从袋中摸出的2个球中含有红球”为事件A
则
（II）记“从袋中摸出的2个球都是红球”为事件B
则
3次摸球恰好有两次中大奖相当于作了3次独立重复实验
则
19、(本题满分12分)
解：（I）设等差数列{log2(an−1)}的公差为d
第一项为 log2(a1−1)=1 第三项为 log2(a3−1)=3
∴公差d=1
∴log2(an−1)=1+(n−1)·1=n ∴an−1=2n
∴an=2n+1
（II）∵
∴
20、（本题满分12分）
解法一：
⑴ 连结AC、BD，设
.由P－ABCD与Q－ABCD都是正四棱锥，
所以PO⊥平面ABCD，QO⊥平面ABCD.从而P、O、Q三点在一条直线上，
所以PQ⊥平面ABCD.
由题设知，ABCD是正方形，所以
．
⑵ 由⑴，
平面
，故可以分别以直线CA、DB、QP为轴，
轴，
轴建立空间直角坐标系（如上图），由题设条件，相关各点的坐标分别是
，
，
,所以
,
,
于是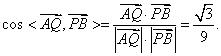
从而异面直线AQ与PB所成的角是
.
⑶ 由⑵，点D的坐标是（0，－
，0），
，
，
设
是平面QAD的一个法向量，
由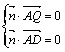
得
.取x=1，得
.
所以点P到平面QAD的距离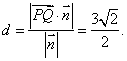
.
解法二：
⑴ 取AD的中点M，连结PM，QM.因为P－ABCD与Q－ABCD都是正四棱锥，
所以AD⊥PM，AD⊥QM. 从而AD⊥平面PQM.
又
平面PQM，所以PQ⊥AD.同理PQ⊥AB，所以PQ⊥平面ABCD.
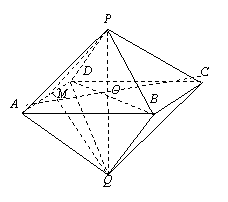⑵ 连结AC、BD设，由PQ⊥平面ABCD及
正四棱锥的性质可知O在PQ上，从而P、A、Q、C四
点共面.取OC的中点N，连结PN．
因为
，所以
，
从而AQ∥PＮ.∠BPＮ（或其补角）是异面直线AQ
与PB所成的角.连接BN，
因为
．
所以
．
从而异面直线AQ与PB所成的角是．
⑶ 由⑴知，AD⊥平面PＱM，所以平面PＱM⊥平面QAD. 过Ｐ作ＰＨ⊥ＱＭ于Ｈ，
则ＰＨ⊥平面QAD，所以ＰＨ的长为点P到平面QAD的距离．
连结OM，则
.所以
，
又ＰＱ＝ＰＯ＋ＱＯ＝３，于是
.
即点P到平面QAD的距离是
.
21、(本小题满分12分)
（1）证明：由抛物线定义知
，（2分）
，可得PQ所在直线方程为x0x=2(y+y0)，
得Q点坐标为(0, -y0)，∴
，
∴ PF=QF， ∴△PFQ为等腰三角形．
（2）设A(x1, y1)，B(x2,
y2)，又M点坐标为(0, y0)， ∴AB方程为
，
由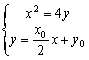
得
……①
由
得：
，
∴
……②
由①②知
，得
，由x0≠0可得x2≠0，
∴
，又
，解得：
．
21、（本小题满分14分）
解：（1）∵
，配方得
，由
得最大值
。
∴
，
。
（2）要使
，
。可以使①
中有3个元素，
中有2个元素， 
中有1个元素。则
。
②中有6个元素，中有4个元素， 中有2个元素。则
（3）由（2）知
