高考文科数学模拟试题（1）
一、选择题(本大题共10小题，每小题5分，共5 0分. 在每小题给出的四个选项中，只有一项是符合题目要求的).
1． 设全集为 R ，A =
，则
( )．
| A． | B.｛x x＞0｝ | C.｛x x | D. |
｝
2． 
等于( )．
| A．2-2i | B．2+2i | C．-2 | D．2 |
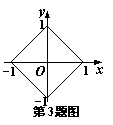3． 设
是图中的四边形内的点或四边形边界上的点，则
的最大值是( )．
| A． | B． | C． | D． |
4． 抛物线
的焦点坐标是( )．
| A．（a , 0） | B．(-a, 0) | C．（0, a） | D．（0, - a） |
5． 若函数
的一个正数零点附近的函数值用二分法计算，其参考数据如下：
| f(1)=-2 | f(1.5)=0.625 | f(1.25)=-0.984 |
| f(1.375)=-0.260 | f(1.4375)=0.162 | f(1.40625)=-0.054 |
那么方程
的一个近似根（精确到0.1）为( )．
| A. 1.2 | B. 1.3 | C. 1.4 | D. 1.5 |
6． 已知
、
是两条不同直线，
、
是两个不同平面，有下列4个命题：
① 若
，则m∥； ② 若
，则
；
③ 若
，则
；
④ 若
是异面直线，
，则.
其中正确的命题有( )．
| A．①② | B．②③ | C．③④ | D．②④ |
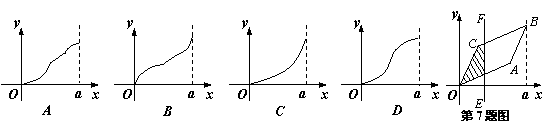7． 如图，垂直于x轴的直线EF经坐标原点O向右移动. 若E是EF与x 轴的交点，设OE =x
)，EF在移动过程中扫过平行四边形OABC的面积为
(图中阴影部分)，则函数
的图象大致是( )．
8． 
的内角A、B、C的对边分别为a、b、c，若a、b、c成等比数列，且
，
| A． | B． | C． | D． |
则
( )．
9． 已知函数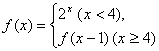
，那么
的值为( )．
| A．32 | B．16 | C．8 | D．64 |
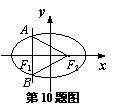10．已知点F1、F2分别是椭圆
的左、右焦点，过F1且垂直于x轴的直线与椭圆交于A、B两点，若△ABF2为正三角形，则该椭圆的离心率
为( )．
|
| A． | B . | C. | D . |
二、填空题(本大题共4小题，每小题5分，共20分，请把答案填在题中的横线上).
11. 如果实数
,且
,那么
、
和
由大到小的顺序是 .
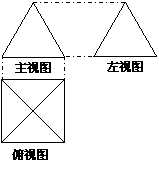
12．如图，一个简单空间几何体的三视图其主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形，则其体积是____.
|
14．考察下列一组不等式：
.
将上述不等式在左右两端仍为两项和的情况下加以推广，使以上的不等式成为推广不等式的特例，则推广的不等式可以是 .
三、解答题(满分80分，解答应写出文字说明和演算步骤).
15.（本小题满分12分）
已知：
，
，x
R.
求
的最大值，并求使取得最大值时
和
的夹角．
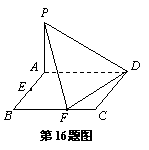16．（本小题满分14分）
已知ABCD是矩形，
，E、F分别是线段AB、BC的中点，
面ABCD.
(1) 证明：PF⊥FD；
(2) 在PA上找一点G，使得EG∥平面PFD.
17．（本小题满分12分）
已知，圆C：
，直线
：
.
(1) 当a为何值时，直线与圆C相切；
(2) 当直线与圆C相交于A、B两点，且
时，求直线的方程.
18．（本小题满分14分）
设数列
的前项和为
，且
，数列
为等差数列，且
，
.
(1) 求
；
(2) 求数列的通项公式；
(3) 若
，求数列
的前项和
19．（本小题满分14分）
为了对2006年佛山市中考成绩进行分析，在60分以上的全体同学中随机抽出8位，他们的数学(已折算为百分制)、物理、化学分数对应如下表，
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
| 化学分数z | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
(1) 若规定85分(包括85分)以上为优秀，求这8位同学中数学和物理分数均为优秀的概率；
(2) 用变量y与x、z与x的相关系数说明物理与数学、化学与数学的相关程度；
(3) 求y与x、z与x的线性回归方程（系数精确到0.01），并用相关指数比较所求回归模型的效果.
参考数据：
，
，
，
，
，
，
，
，
，
，
.
20．（本小题满分14分）
已知函数
.
(1) 当
时，求函数
的单调区间和极值；
(2) 若
在
上是单调函数，求实数a的取值范围.
数学试题参考答案和评分标准（文科1）
一、选择题（每题5分，共40分）
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | D | D | A | C | B | A | B | C | D |
二、填空题（每题5分，共30分）
11．＜＜ 12．
13．
14．
（或
为正整数）注：填
以及是否注明字母的取值符号和关系，均不扣分．
三、解答题(满分80分，解答应写出文字说明和演算步骤).
15. 解：∵
， ……………………………………………4分
∴当
即
时， ……………………………………………6分
取得最大值2. ……………………………………………………………………………………………8分
此时，
，故
，………………………………………11分
∴和的夹角是0. …………………………………………………………………………………………12分
注：也可以由和同向来说明.
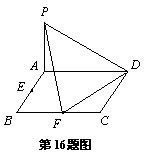
16．解：(1) 证明：连结AF，
∵在矩形ABCD中，，F是线段BC的中点，
∴AF⊥FD. …………………………………………………………………3分
又∵PA⊥面ABCD，∴PA⊥FD. …………………………………4分
∴平面PAF⊥FD. …………………………………………………………5分
∴PF⊥FD. …………………………………………………………………6分
(2) 过E作EH∥FD交AD于H，则EH∥平面PFD且
. …………9分
再过H作HG∥DP交PA于G，则HG∥平面PFD且
. ……………11分
∴平面EHG∥平面PFD.
∴EG∥平面PFD. ……………………………………………………………………………………………13分
从而满足的点G为所找. ………………………………………………………………14分
注：1. 也可以延长DF、AB交于R，然后找EG∥PR进行处理)
2. 本题也可用向量法解.
17．解：将圆C的方程配方得标准方程为
，则此圆的圆心为（0 , 4），半径为2.
(1) 若直线与圆C相切，则有
. ………………………………………………3分
解得
. ……………………………………………………………………………………………………5分
(2) 解法一：过圆心C作CD⊥AB，则根据题意和圆的性质，得
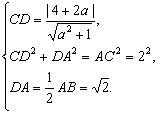……………………………………………………………………………8分
解得
. ………………………………………………………………………………………………10分
（解法二：联立方程
并消去，得
.
设此方程的两根分别为
、
，则用
即可求出a.）
∴直线的方程是
和
. ………………………………………12分
18．解：（1）由
，令
，则
，又
，所以
.
由
，得
.
由
，得
. ……………………………………………………………………3分
（2）方法一：当
时，由，可得
.
即
. …………………………………………………………………………………………………………………………5分
所以是以为首项，
为公比的等比数列，于是
. ……………6分
方法二：由（1）归纳可得，，它适合.
所以. ……………………………………………………………………………………………………………5分
注：方法二扣1分.
（3）数列为等差数列，公差
,可得
. ……………8分
从而
，………………………………………………9分
∴
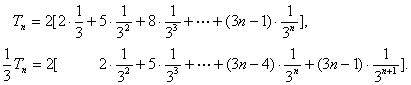……………10分
∴
. …………………11分
∴
. ……………………………………………………………14分
19．解：(1) 由表中可以看出，所选出的8位同学中，数学和物理分数均为优秀的人数是3人，其概率是
. ………………………………………………………………………………………………………3分
(2) 变量y与x、z与x的相关系数分别是
、
. ……………………………………………5分
可以看出，物理与数学、化学与数学的成绩都是高度正相关. …………………………6分
(3) 设y与x、z与x的线性回归方程分别是
、
.
根据所给的数据，可以计算出
，
. ……………………………………………………10分
所以y与x和z与x的回归方程分别是
、
. …………………………………………………………11分
又y与x、z与x的相关指数是
、
. ……13分
故回归模型
比回归模型
的拟合的效果好. …14分
20．解：(1) 易知，函数的定义域为
. ……………………………………………1分
当时，
. ……………………………………………2分
当x变化时，
和的值的变化情况如下表： ……………………………………4分
| x | （0,1） | 1 | （1，+∞） |
|
| - | 0 | + |
|
| 递减 | 极小值 | 递增 |
由上表可知，函数的单调递减区间是（0,1）、单调递增区间是（1，+∞）、极小值是
. ……………………………………………………………………………………………………………7分
(2) 由
，得
. ………………………………8分
又函数为
上单调函数，
① 若函数
为上的单调增函数，则
在上恒成立，即不等式
在上恒成立.也即
在上恒成立. ………11分
又
在上为减函数，
. ……………………12分
所以
.
② 若函数为上的单调减函数，则
在上恒成立，这是不可能的. ……………………………………………………………………………………………………………………13分
综上，
的取值范围为
. ………………………………………………………………………14分