高中数学毕业招生全国统一考试
数学(文史类)
本试卷分第I卷(选择题)和第II(非选择题)两部分,第I卷1至2页,第II卷3至9页,共150分.考试时间120分钟.考试结束,将本试卷和答题卡一并交回.
第I卷(选择题 共40分)
注意事项:
1.答第I卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案.不能答在试卷上.
一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
1.已知![]() ,那么角
,那么角![]() 是( )
是( )
A.第一或第二象限角 B.第二或第三象限角
C.第三或第四象限角 D.第一或第四象限角
2.函数![]() 的反函数的定义域为( )
的反函数的定义域为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.函数![]() 的最小正周期是( )
的最小正周期是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.椭圆![]() 的焦点为
的焦点为![]() ,
,![]() ,两条准线与
,两条准线与![]() 轴的交点分别为
轴的交点分别为![]() ,若
,若![]() ,则该椭圆离心率的取值范围是( )
,则该椭圆离心率的取值范围是( )
A.![]() B.
B.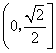 C.
C.![]() D.
D.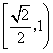
5.某城市的汽车牌照号码由2个英文字母后接4个数字组成,其中4个数字互不相同的牌照号码共有( )
A.![]() 个 B.
个 B.![]() 个
个
C.![]() 个 D.
个 D.![]() 个
个
6.若不等式组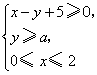 表示的平面区域是一个三角形,则
表示的平面区域是一个三角形,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
7.平面![]() 平面
平面![]() 的一个充分条件是( )
的一个充分条件是( )
A.存在一条直线![]()
B.存在一条直线![]()
C.存在两条平行直线![]()
D.存在两条异面直线![]()
8.对于函数①![]() ,②
,②![]() ,③
,③![]() ,判断如下两个命题的真假:
,判断如下两个命题的真假:
命题甲:![]() 是偶函数;
是偶函数;
命题乙:![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;
上是增函数;
能使命题甲、乙均为真的所有函数的序号是( )
A.①② B.①③ C.② D.③
数学(文史类)
第II卷(共110分)
注意事项:
1.用钢笔或圆珠笔将答案直接写在试卷上.
2.答卷前将密封线内的项目填写清楚.
二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.
9.![]() 是
是![]() 的导函数,则
的导函数,则![]() 的值是 .
的值是 .
10.若数列![]() 的前
的前![]() 项和
项和![]() ,则此数列的通项公式为 .
,则此数列的通项公式为 .
11.已知向量![]() .若向量
.若向量![]() ,则实数
,则实数![]() 的值是 .
的值是 .
12.在![]() 中,若
中,若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
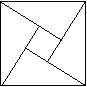 13.2002年在北京召开的国际数学家大会,会标是我国以古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为
13.2002年在北京召开的国际数学家大会,会标是我国以古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为![]() ,那么
,那么![]() 的值等于 .
的值等于 .
14.已知函数![]() ,
,![]() 分别由下表给出
分别由下表给出
|
| 1 | 2 | 3 |
|
| 2 | 1 | 1 |
|
| 1 | 2 | 3 |
|
| 3 | 2 | 1 |
则![]() 的值为 ;当
的值为 ;当![]() 时,
时,![]() .
.
三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.
15.(本小题共12分)
记关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,不等式
,不等式![]() 的解集为
的解集为![]() .
.
(I)若![]() ,求
,求![]() ;
;
(II)若![]() ,求正数
,求正数![]() 的取值范围.
的取值范围.
16.(本小题共13分)
数列![]() 中,
中,![]()
![]() (
(![]() 是常数,
是常数,![]() ),且
),且![]() 成公比不为
成公比不为![]() 的等比数列.
的等比数列.
 (I)求
(I)求![]() 的值;
的值;
(II)求![]() 的通项公式.
的通项公式.
17.(本小题共14分)
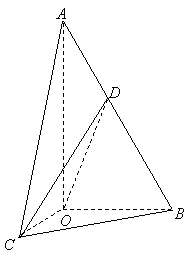
如图,在![]() 中,
中,![]() ,斜边
,斜边![]() .
.![]() 可以通过
可以通过![]() 以直线
以直线![]() 为轴旋转得到,且二面角
为轴旋转得到,且二面角![]() 的直二面角.
的直二面角.![]() 是
是![]() 的中点.
的中点.
(I)求证:平面![]() 平面
平面![]() ;
;
(II)求异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
18.(本小题共12分)
某条公共汽车线路沿线共有11个车站(包括起点站和终点站),在起点站开出的一辆公共汽车上有6位乘客,假设每位乘客在起点站之外的各个车站下车是等可能的.求:
(I)这6位乘客在其不相同的车站下车的概率;
(II)这6位乘客中恰有3人在终点站下车的概率;
19.(本小题共14分)
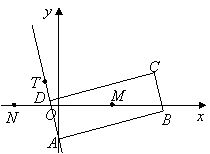 如图,矩形
如图,矩形![]() 的两条对角线相交于点
的两条对角线相交于点![]() ,
,![]() 边所在直线的方程为
边所在直线的方程为![]() 点
点![]() 在
在![]() 边所在直线上.
边所在直线上.
(I)求![]() 边所在直线的方程;
边所在直线的方程;
(II)求矩形![]() 外接圆的方程;
外接圆的方程;
(III)若动圆![]() 过点
过点![]() ,且与矩形
,且与矩形![]() 的外接圆外切,求动圆
的外接圆外切,求动圆![]() 的圆心的轨迹方程.
的圆心的轨迹方程.
20.(本小题共14分)
已知函数![]() 与
与![]() 的图象相交于
的图象相交于![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的图象在
的图象在![]() 两点的切线,
两点的切线,![]() 分别是
分别是![]() ,
,![]() 与
与![]() 轴的交点.
轴的交点.
(I)求![]() 的取值范围;
的取值范围;
(II)设![]() 为点
为点![]() 的横坐标,当
的横坐标,当![]() 时,写出
时,写出![]() 以
以![]() 为自变量的函数式,并求其定义域和值域;
为自变量的函数式,并求其定义域和值域;
(III)试比较![]() 与
与![]() 的大小,并说明理由(
的大小,并说明理由(![]() 是坐标原点).
是坐标原点).
参考答案
一、选择题(本大题共8小题,每小题5分,共40分)
1.C 2.B 3.B 4.D 5.A 6.C
7.D 8.C
二、填空题(本大题共6小题,每小题5分,共30分)
9.![]() 10.
10.![]() 11.
11.![]() 12.
12.![]()
13.![]() 14.
14.![]()
![]()
三、解答题(本大题共6小题,共80分)
15.(共12分)
解:(I)由![]() ,得
,得![]() .
.
(II)![]() .
.
由![]() ,得
,得![]() ,又
,又![]() ,所以
,所以![]() ,
,
即![]() 的取值范围是
的取值范围是![]() .
.
16.(共13分)
解:(I)![]() ,
,![]() ,
,![]() ,
,
因为![]() ,
,![]() ,
,![]() 成等比数列,
成等比数列,
所以![]() ,
,
解得![]() 或
或![]() .
.
当![]() 时,
时,![]() ,不符合题意舍去,故
,不符合题意舍去,故![]() .
.
(II)当![]() 时,由于
时,由于
![]() ,
,
![]() ,
,
![]()
![]() ,
,
所以![]() .
.
又![]() ,
,![]() ,故
,故![]() .
.
当![]() 时,上式也成立,
时,上式也成立,
所以![]() .
.
 17.(共14分)
17.(共14分)
解法一:
(I)由题意,![]() ,
,![]() ,
,
![]() 是二面角
是二面角![]() 是直二面角,
是直二面角,
![]() ,又
,又![]() ,
,
![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() .
.
![]() 平面
平面![]() 平面
平面![]() .
.
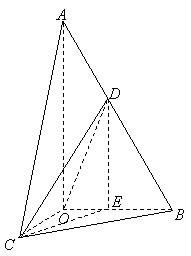
(II)作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() (如图),则
(如图),则![]() ,
,
![]() 是异面直线
是异面直线![]() 与
与![]() 所成的角.
所成的角.
在![]() 中,
中,![]() ,
,![]() ,
,
![]() .
.
又![]() .
.
![]() 在
在![]() 中,
中,![]() .
.
![]() 异面直线
异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.
解法二:
(I)同解法一.
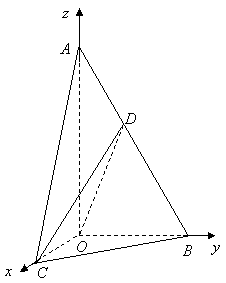 (II)建立空间直角坐标系
(II)建立空间直角坐标系![]() ,如图,则
,如图,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
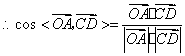
![]() .
.
![]() 异面直线
异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.
18.(共13分)
解:(I)这6位乘客在互不相同的车站下车的概率为
![]() .
.
(II)这6位乘客中恰有3人在终点站下车的概率为![]() .
.
19.(共14分)
解:(I)因为![]() 边所在直线的方程为
边所在直线的方程为![]() ,且
,且![]() 与
与![]() 垂直,所以直线
垂直,所以直线![]() 的斜率为
的斜率为![]() .
.
又因为点![]() 在直线
在直线![]() 上,
上,
所以![]() 边所在直线的方程为
边所在直线的方程为![]() .
.
![]() .
.
(II)由![]() 解得点
解得点![]() 的坐标为
的坐标为![]() ,
,
因为矩形![]() 两条对角线的交点为
两条对角线的交点为![]() .
.
所以![]() 为矩形
为矩形![]() 外接圆的圆心.
外接圆的圆心.
又![]() .
.
从而矩形![]() 外接圆的方程为
外接圆的方程为![]() .
.
(III)因为动圆![]() 过点
过点![]() ,所以
,所以![]() 是该圆的半径,又因为动圆
是该圆的半径,又因为动圆![]() 与圆
与圆![]() 外切,
外切,
所以![]() ,
,
即![]() .
.
故点![]() 的轨迹是以
的轨迹是以![]() 为焦点,实轴长为
为焦点,实轴长为![]() 的双曲线的左支.
的双曲线的左支.
因为实半轴长![]() ,半焦距
,半焦距![]() .
.
所以虚半轴长![]() .
.
从而动圆![]() 的圆心的轨迹方程为
的圆心的轨迹方程为![]() .
.
20.(本小题共14分)
解:(I)由方程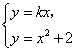 消
消![]() 得
得![]() .···················· ①
.···················· ①
依题意,该方程有两个正实根,
故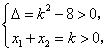 解得
解得![]() .
.
(II)由![]() ,求得切线
,求得切线![]() 的方程为
的方程为![]() ,
,
由![]() ,并令
,并令![]() ,得
,得![]()
![]() ,
,![]() 是方程①的两实根,且
是方程①的两实根,且![]() ,故
,故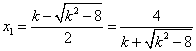 ,
,![]() ,
,
![]() 是关于
是关于![]() 的减函数,所以
的减函数,所以![]() 的取值范围是
的取值范围是![]() .
.
![]() 是关于
是关于![]() 的增函数,定义域为
的增函数,定义域为![]() ,所以值域为
,所以值域为![]() ,
,
(III)当![]() 时,由(II)可知
时,由(II)可知![]() .
.
类似可得![]() .
.![]() .
.
由①可知![]() .
.
从而![]() .
.
当![]() 时,有相同的结果
时,有相同的结果![]() .
.
所以![]() .
.