高考数学创新试题及考点预测(一)
数学试题
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中, 只有一项是符合题目要求的)
1.已知集合![]() ,
,![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.某单位有业务人员120人,管理人员24人,后勤人员16人。现用分层抽样的方法,
从该单位职工中抽取一个容量为![]() 的样本,已知从管理人员中抽取了3人,则
的样本,已知从管理人员中抽取了3人,则![]() 为
为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. 已知圆![]() 上存在两点关于直线
上存在两点关于直线![]() 对称,则实数
对称,则实数![]() 为
为
A.![]() B.
B.![]() C.
C.![]() D. 无法确定
D. 无法确定
4. 下列函数中周期是2的函数是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.已知直线m、n及平面α、β,则下列命题正确的是
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
6.在空间直角坐标系![]() 中,
中,![]() 、
、![]() 、
、 ![]() 分别是
分别是![]() 轴、
轴、![]() 轴、
轴、![]() 轴的方向向量,
轴的方向向量,
设![]() 为非零向量,且
为非零向量,且![]() ,
,![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知A、B、C、D是同一球面上的四点,且每两点间距离都等于2,
则球心到平面BCD的距离是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知点![]() 分别是椭圆
分别是椭圆![]()
![]() 为参数,
为参数,![]() 的右顶点和左焦点,
的右顶点和左焦点,
点![]() 为椭圆的一个短轴端点,若
为椭圆的一个短轴端点,若![]() ,则椭圆的离心率
,则椭圆的离心率![]() 为
为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.若关于![]() 的不等式组
的不等式组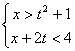 的解集不是空集,则实数
的解集不是空集,则实数![]() 的取值不可能是
的取值不可能是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
| 第1行 | 1 |
| 第2行 | 2、3 |
| 第3行 | 4、5、6、7 |
| …… | …… |
10.如图是一个由正整数组成的数表,表中下
一行数的个数是其上一行中数的个数
的2倍,则表中第8行的第5个数是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.设![]() ,若实数
,若实数![]() 满足条件
满足条件![]() ,则
,则![]() 的最大值是
的最大值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
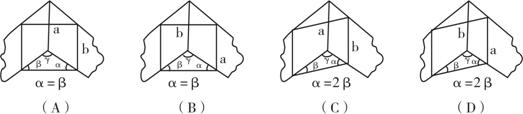
12. 用一块长为a,宽为b(a>b)的矩形木板,在二面角为![]() 的墙角处,围出一个直三棱柱的谷仓,在下面四种设计中,容积最大的是( )
的墙角处,围出一个直三棱柱的谷仓,在下面四种设计中,容积最大的是( )
第Ⅱ卷(非选择题,共100分)
二、填空题(本大题共4小题,每小题4分,共16分. 答案填在题中横线上.)
13.已知![]() 展开式中的第5项等于
展开式中的第5项等于![]() ,那么
,那么![]() __________________
__________________
14.已知数列{xn}中,![]() ,则x2006= .
,则x2006= . 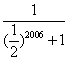
15.已知函数![]() 在
在![]() 上是减函数,且满足
上是减函数,且满足![]() ,
,![]() ,
,
那么![]() 的解集为 ________________
的解集为 ________________![]()
16.已知直线![]() 和
和![]() 将曲线
将曲线![]() ,(
,(![]() 为参数,
为参数,![]() )所围成的区域分成若干部分,现用5种不同的颜色给每部分涂色,每一部分只涂一种颜色,且任意两部分的颜色各不相同,若一共有120种不同的法,则实数
)所围成的区域分成若干部分,现用5种不同的颜色给每部分涂色,每一部分只涂一种颜色,且任意两部分的颜色各不相同,若一共有120种不同的法,则实数![]() 的取值范围是__________
的取值范围是__________
三、解答题(本大题共6小题,每小题英才苑14分,满分84分.解答应写出文字说明,证明过程或演算步骤.)
17.△ABC的三边为a,b,c,已知![]() ,且
,且![]() ,
,
求![]() 的值及三角形面积
的值及三角形面积![]() 的最大值.
的最大值.
18.福建省的地方汽车牌照号码为七位码,从左边起第一个位置是表示福建省的汉字“闽” ;
第二个位置是代表城市的字母(如A代表福州市、D代表厦门市等);后五个位置是
汽车的编号,编号规则如下:按照汽车落户的先后顺序,从左边起由0 ~ 9这10个数
字排成五位数字码;当五位数字码排满后,对之后落户的汽车,从左边起的第三、第
四位置按除I、Q以外的24个英文字母依次编码,第五至第七位位置仍由数字0 ~ 9
依次编码,下图就表示福州市编号为W6691的车辆。福州市区出租车的号码标志是
第三位置的编码为T,例如“闽A![]() TM996”。假定按上述规则确定的每一个编码对
TM996”。假定按上述规则确定的每一个编码对
应一辆落户汽车(即假定福州市地方汽车已排满所有编号),从成都市的地方汽车中
任意抽取一辆。
⑴ 抽到的牌照号码恰好是福州市区的出租车的概率是多少?
⑵ 抽到的牌照号码在“闽A![]() 99999”之前且最后一个数字为偶数的概率是多少?
99999”之前且最后一个数字为偶数的概率是多少?
⑶ 抽到的牌照号在“闽A![]() GZ999”之前且后三位置上每个数字都是偶数的概率是多少?
GZ999”之前且后三位置上每个数字都是偶数的概率是多少?
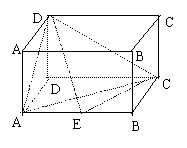
19.如图,在长方体![]() 中,
中,![]() 点E在棱AB上移动.
点E在棱AB上移动.
(I)证明:![]() ;
;
(II)若E为AB中点,求E到面![]() 的距离;
的距离;
(III)AE等于何值时,二面角![]() 的大小为
的大小为![]()
 |
20.设![]() 是函数
是函数![]() 的两个极值点。
的两个极值点。
⑴求证:![]() ;
;
⑵若![]() ,求证:
,求证:![]() 。
。
21. 已知数列![]() 满足
满足![]() 且对一切
且对一切![]() 有
有![]() +……
+……![]() ,
,
(1)求证:对一切![]() 有
有![]()
(2)求数列![]() 的通项公式
的通项公式
(3)求证:![]() ……
……![]()
22.已知倾斜角为![]() 的直线
的直线![]() 过点
过点![]() 和点
和点![]() ,点
,点![]() 在第一象限,
在第一象限,![]() 。
。
(1)求点![]() 的坐标;
的坐标;
(2)若直线![]() 与双曲线
与双曲线![]() 相交于
相交于![]() 两点,且线段
两点,且线段![]() 的中点
的中点
坐标为![]() ,求
,求![]() 的值;
的值;
(3)对于平面上任一点![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,称
上运动时,称![]() 的最小值为
的最小值为![]() 与
与
线段![]() 的距离。已知
的距离。已知![]() 在
在![]() 轴上运动,写出点
轴上运动,写出点![]() 到线段
到线段![]() 的距离
的距离![]()
关于![]() 的函数关系式。
的函数关系式。
![]() 2008年高考创新试题及考点预测(一)
2008年高考创新试题及考点预测(一)
数学试题 参考答案
一、选择题(本大题共10小题,每小题5分,共50分)
1—5:DAACD 6—10:CBACB 11—12 DA
二、填空题(本大题有4小题,每小题4分,共16分)
13.2 14. 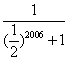 15.
15. ![]() 16.
16.
三、解答题:(本大题有6小题,每小题14分,共84分)
17.解:![]() ,又由余弦定理得
,又由余弦定理得
![]()
![]() .
.![]() ,
,![]() ,得
,得![]() ,
,![]() .又
.又![]() ,
,![]()
![]() .
.
当且仅当![]() 时,等号成立.
时,等号成立.![]()
![]() .
.
18. 解:按照规则,福州市地方汽车的牌照号码共有![]() 个。
个。
⑴ 福州市区出租车的牌照号码共有![]() 个,故抽到的牌照号码恰好是出
个,故抽到的牌照号码恰好是出
租车的概率是![]()
⑵ 牌照号码在“闽A![]() 99999”之前即是汽车的编码仅由0 ~ 9这10个数字
99999”之前即是汽车的编码仅由0 ~ 9这10个数字
组成,其中最后一个数字为偶数的号码有![]() 个,
个,
故所求概率![]()
⑶ 牌照号码在“闽A![]() GZ999”之前,即第三个位置由数字0 ~ 9及A、B、C、D、
GZ999”之前,即第三个位置由数字0 ~ 9及A、B、C、D、
E、 F、G中一个占据,共有17种可能,第四个位置有34种可能,
故号码在“闽A![]() GZ999”之前且最后三个位置为偶数的牌照号码共有
GZ999”之前且最后三个位置为偶数的牌照号码共有![]() 个,
个,
故所求概率为![]()
19.方法一
(I)证明:![]()
(II)设点E到平面![]() 的距离为h,由题设可得
的距离为h,由题设可得![]()
![]() 算得
算得![]()
![]() 则
则![]()
(III)过D作![]() ,垂足为H,连
,垂足为H,连![]() 则
则![]()
![]() 为二面角
为二面角![]() 的平面角.
的平面角.
设![]() ,在直角
,在直角![]() 中,
中,![]()
![]() 在直角
在直角![]() 中,
中,![]() 在直角
在直角![]() 中,
中,![]()
在直角![]() 中,
中,![]() ,在直角
,在直角![]() 中,
中,![]()
![]()
因为以上各步步步可逆,所以当![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]()
方法二:以DA,DC,DD1建立空间坐标系,设![]() ,有
,有![]()
![]()
(I)证明:因为![]() ,所以,
,所以,![]()
(II)解:E是AB中点,有![]()
![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() 则
则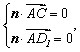 也即
也即![]() ,
,
得![]() ,从而
,从而![]() ,点E到平面
,点E到平面![]() 的距离
的距离![]()
(III)设平面![]() 的法向量为
的法向量为![]()
![]() 由
由![]() 令
令![]() ,得
,得![]()
则![]() 于是
于是![]()
![]() (不合,舍去),
(不合,舍去),![]()
即![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]()
20. 解:由已知:![]()
故![]() 是方程
是方程![]() 的两根,则
的两根,则![]()
由于![]() 故
故![]() 即
即![]()
由于![]()
![]() 得
得![]() 所以
所以![]()
21. 解:(1)由![]() +……
+……![]() 得
得![]() +……+
+……+![]()
相减得:![]()
![]() ·
·![]()
![]()
![]() …………4分
…………4分
(2)由(1)知![]() 得
得![]() (
(![]() ≥2)
≥2)
又![]() 时
时![]() ,由
,由![]()
![]()
![]()
![]()
![]() 为等差数列且
为等差数列且![]() =
=![]() ………………8分
………………8分
(3)![]() …………12分
…………12分
22. 解:(1)设![]() ,
,![]()
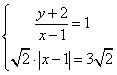 ,
, ![]()
![]() ---------3分
---------3分
(2)设![]()
由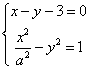 得
得![]() ,-----------------4分
,-----------------4分
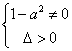
![]() -----------------6分
-----------------6分
![]() ,
,![]() ----------------8分
----------------8分
(3)设线段![]() 上任意一点
上任意一点![]()
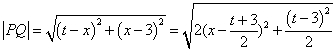 ---------------10分
---------------10分
![]()
![]() 当
当![]() 时,即
时,即![]() 时,当
时,当![]() 时,
时,![]() ;
;
当![]() 时,即
时,即![]() 时,当
时,当![]() 时,
时,![]() ;
;
当![]() 时,即
时,即![]() 时,当
时,当![]() 时,
时,![]() 。--13分
。--13分
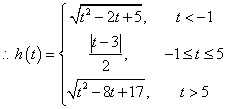 -----------------14分
-----------------14分