高三数学直线与圆单元练习卷（7）
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题意要求的。
1、曲线
关于直线
对称的曲线
的方程为
（
）
A、
B、
C、
D、
2、直线
截圆
所得的劣弧所对的圆心角为 （
）
A、
B、
C、
D、
3、如果
满足
，那么
的最大值是
（
）
A、10 B、8 C、
D、
4、与点
相距为5，且到Y轴的距离等于4的点的个数是
（
）
A、2 B、3 C、4 D、0
5、设集合
当
时，
的取值范围是
（ ）
A、
B、
C、
D、
6、在
中，三内角
所对的边是
且
成等差数列，那么直线
与直线
的位置关系是 （ ）
A、平行 B、重合 C、垂直 D、相交但不垂直
7、若关于
的方程
有且只有两个不同的实数根，则实数
的取值范围是
（ ）
A、
B、
C、
D、
8、已知圆
和直线
的交点分别为
、
两点,
为坐标原点,则
的值为
(
)
A、
B、
C、5 D、10
9、若直线
（
R）始终平分圆
的周长，则
的取值范围是
(
)
A、（0，1） B、（0，1］ C、（－∞，1） D、（－∞，1］
10、设△ABC的一个顶点是A（3，－1），∠B，∠C的平分线方程分别是x=0，y=x，则直线BC的方程是 （ ）
A．y=2x+5 B．y=2x+3 C．y=3x+5 D．
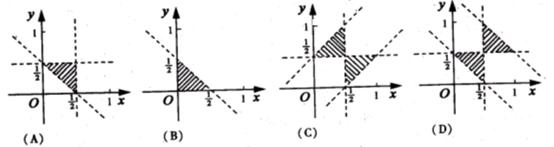
11、设集合A＝{(x，y)x，y，1－x－y是三角形的三边长}，则A所表示的平面区域(不含边界的阴影部分)是 ( )
12、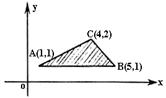
在如图所示的坐标平面的可行域（阴影部分且
包括边界）内，目标函数
取得最
大值的最优解有无数个，则a为 （ ）
A．－2 B．2 C．－6 D．6
二、填写题：本大题共4小题，每小题4分，共16分。把答案填在答题卡相应位置。
13、已知θ∈R，则直线
的倾斜角的取值范围是___________
14、已知直线ax＋by＋c＝0与圆O：x2＋y2＝1相交于A、B两点，且AB＝
，则
＝ .
15、已知两圆
和
相交于
两点．若
点的坐标为（1，2），则
点的坐标为
．
16、当
时，要使动直线
的点都在横轴的上方（不包括横轴），则实数的范围为__________________
三、解答题：本大题共6小题，共74分。解答应写出文字说明、证明过程或演算步骤。
17、（本小题满分12分）自点（－3，3）发出的光线L射到x轴上，被x轴反射，其反射线所在直线与圆
相切，求光线L所在直线方程．
18、（本小题满分12分）某工厂的一个车间生产某种产品，其成本为每公斤27元，售价为每公斤50元。在生产产品的同时，每公斤产品产生出0.3立方米的污水,污水有两种排放方式:其一是输送到污水处理厂,经处理(假设污水处理率为85%)后排入河流;其二是直接排入河流.若污水处理厂每小时最大处理能力是0.9立方米污水,处理成本是每立方米污水5元;环保部门对排入河流的污水收费标准是每立方米污水17.6元,根据环保要求该车间每小时最多允许排入河流中的污水是0.225立方米.试问:该车间应选择怎样的生产与排污方案,才能使其净收益最大.
19、（本小题满分12分）已知x2+y2=9的内接△ABC中，A点的坐标是（－3，0），重心G的坐标是
，求：
（1）直线BC的方程；（2）弦BC的长度.
.
20、（本小题满分12分）已知曲线C：x2+y2-2x-4y+m=0
（1）当m为何值时，曲线C表示圆；
（2）若曲线C与直线x+2y-4=0交于M、N两点，且OM⊥ON(O为坐标原点)，求m的值。
21、（本小题满分12分）已知圆M：2x2+2y2－8x－8y－1＝0和直线l：x+y－9＝0过直线 上一点A作△ABC，使∠BAC=45°，AB过圆心M，且B，C在圆M上。
⑴当A的横坐标为4时，求直线AC的方程；
⑵求点A的横坐标的取值范围。
22、（本小题满分14分）已知圆(x+4)2+y2=25的圆心为M1，圆(x－4)2+y2=1的圆心为M2，一动圆与这两个圆都外切.
（1）求动圆圆心P的轨迹方程；
（2）若过点M2的直线与（1）中所求轨迹有两个交点A、B，求AM1·BM1的取值范围.
答案：
DCABC BACDA AA
13、
14、
15、
16、
17、 3x＋4y－3＝0，或4x＋3y＋3＝0
18、该车间应每小时生产3.3公斤产品,直接排入河流的污水量为每小时0.09立方米,这样净收益最大.
19、（1）
（2）
20、（1）m<5 （2）m=
21、⑴5x+y－25＝0或x－5y+21＝0 ⑵A点的横坐标范围为［3，6］
22、（1）
－
=1（x≥2） （2）AM1·BM1≥100