高考理科数学模拟试题(理科3)
一、选择题:
1.![]() =
( )
=
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.函数![]() 的定义域是
( )
的定义域是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知点![]() 在不等式组
在不等式组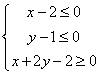 表示的平面区域上运动,则
表示的平面区域上运动,则![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.如图,湖面上有4个相邻的小岛A,B,C,D,现要建3座桥梁将这4个小岛连接起来,共有多少种不同的建桥方案。 ( ) A.20种 B. 4种 C.8种 D.16种
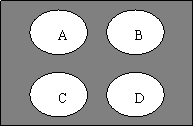
(题4图)
5.![]() ,且
,且![]() ,则向量
,则向量![]() 与
与![]() 的夹角为
( )
的夹角为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知![]() ,则p是q的
( )
,则p是q的
( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
7.若![]() 的方差为3,则
的方差为3,则![]() 的标准差为 ( )
的标准差为 ( )
A.12
B.![]() C.16
D.4
C.16
D.4
8.![]() 是定义在R上的以3为周期的奇函数,且
是定义在R上的以3为周期的奇函数,且![]() ,则方程
,则方程![]() 在区间
在区间![]() 内解的个数的最小值是
( )
内解的个数的最小值是
( )
A.2 B.3 C.4 D.5
第Ⅱ卷
二、填空题:本大题共6小题,每小题5分,共30分,把答案填在相应的横线上。
9.已知![]() 则
则![]() __________.
__________.
10.在R上定义运算![]() ,若不等式
,若不等式![]() 对任意实数x都成立,则
对任意实数x都成立,则![]() 的取值范围是 ( )
的取值范围是 ( )
11.已知![]() >0,二项式
>0,二项式![]() 展开式中常数项为1120,则此展开式中各项系数的和等于 .
展开式中常数项为1120,则此展开式中各项系数的和等于 .
12.已知直线![]() 与圆O:
与圆O:![]() 相交于A,B两点,且AB=
相交于A,B两点,且AB=![]() ,则
,则![]() __________.
__________.
13.若关于x的方程![]() 有三个不同实根,则a的取值范围是________________.
有三个不同实根,则a的取值范围是________________.
14.选做题(1)曲线的参数方程为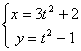 (t是参数),则曲线是____________________
(t是参数),则曲线是____________________
(2).如图,![]() ⊙
⊙![]() 的内接三角形,
的内接三角形,![]() ⊙
⊙![]() 的切线,
的切线,
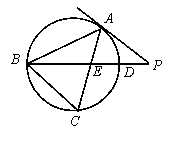
![]() 交
交![]() 于点
于点![]() ,交⊙
,交⊙![]() 于点
于点![]() ,若
,若![]() ,
,
![]() .
.
(3)
已知![]() ,则
,则![]() 的最小值是____________
的最小值是____________
三、解答题:本大题共5小题,共70分,解答应写出文字说明,证明过程或演算步骤。
15. (本小题满分12分) 已知![]() ,求
,求![]() 的值。
的值。
16.(本小题满分12分)某种人群中各种血型的人所占的比如下表所示:
| 血型 | A | B | AB | O |
| 该血型的人所占比% | 28 | 29 | 8 | 35 |
已知同种血型的人可以输血,O型血可以输给任一种血型的人,任何人的血都可以输给AB型血的人,其他不同血型的人不能互相输血。小明是B型血,若小明因病需要输血,问:(1)任找一人,其血可以输给小明的概率是多少?
(2)任找一人,其血不能输给小明的概率是多少?
17.(本小题满分12分)已知函数![]() ,其中
,其中![]() 表示不超过
表示不超过![]() 的最大整数,如:
的最大整数,如:![]() ,
,![]() ,
,![]() 。
。
(1)求![]() 、
、![]() 的值;
的值;
(2)判断函数![]() 的奇偶性;
的奇偶性;
(3)若![]() ,求
,求![]() 的值域。
的值域。
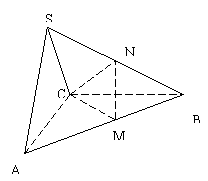 18.(本小题满分15分)在三棱锥
18.(本小题满分15分)在三棱锥![]() 中,△ABC是边长为4的正三角形,平面
中,△ABC是边长为4的正三角形,平面![]() ,
,![]() ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。
(1)证明:![]() ;
;
(2)求二面角N-CM-B的大小;
(3)求点B到平面CMN的距离。
19.(本小题满分16分)设![]() 。
。
(1)是否存在常数p,q,使![]() 为等比数列?若存在,求出p,q的值。若不存在,说明理由;
为等比数列?若存在,求出p,q的值。若不存在,说明理由;
(2)求![]() 的通项公式;
的通项公式;
(3)当![]() 时,证明:
时,证明:![]() 。
。
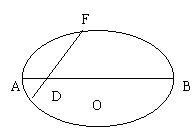 20.(本小题满分15分)如图,已知椭圆长轴端点A、B,弦EF与AB交于点D,O为中心,且
20.(本小题满分15分)如图,已知椭圆长轴端点A、B,弦EF与AB交于点D,O为中心,且![]() ,
,![]() ,
,![]() 。
。
(1)求椭圆的长轴长的取值范围;
(2)若D为椭圆的焦点,求椭圆的方程。
数 学试题(3理科) 参考答案
一、选择题:本大题共8小题,每小题5分,共40分。
1.D 2.A 3.C 4.D 5.C 6.B 7.B 8. D
二、填空题:本大题共6小题,每小题5分,共30分
9. ![]() 10.
10.![]() 11.1 12.
11.1 12.![]() 13.
13.![]() 14.(1) 射线 (2)
14.(1) 射线 (2)![]() (3) 6
(3) 6
三、解答题:本大题共5小题,共70分,解答应写出文字说明,证明过程或演算步骤。
15. ∵ ![]()
∴ ![]()
∴ tanθ=2
∴ ![]()
16.(本小题满分12分)
解:对任一人,其血型为A,B,AB,O型血的事件分别记为![]() ,它们是互斥的。由已知有:
,它们是互斥的。由已知有:
![]() ,因为B,O型血可以输给B型血的人,故“可以输给B型血的人”为事件
,因为B,O型血可以输给B型血的人,故“可以输给B型血的人”为事件![]() ,根据互斥事件的加法公式有:
,根据互斥事件的加法公式有:
![]() =0.29+0.35=0.64
=0.29+0.35=0.64
(2)由于A,AB型血不能输给B型血的人,故“不能输给B型血的人”为事件![]() ,
,
![]() =0.28+0.08=0.36
=0.28+0.08=0.36
答:任找一人,其血可以输给小明的概率是0.64,任找一人,其血不能输给小明的概率是0.36
17.(本小题满分12分)
解:(1)![]()
![]()
(2)由(1)知:![]()
![]() ,且
,且![]()
![]() ,
,
故![]() 为非奇非偶函数。
为非奇非偶函数。
(3)当![]() 时,
时,![]() ,则
,则![]() , 所以
, 所以![]() 可取2,3,4。
可取2,3,4。
当![]() 时,
时,![]() ,则
,则![]() , 所以
, 所以![]() 可取0,1。
可取0,1。
当![]() 时,
时,![]() ,则
,则![]() , 所以
, 所以![]() 。
。
当![]() 时,
时,![]() ,则
,则![]() , 所以
, 所以![]() =1。
=1。
当![]() 时,
时,![]() ,则
,则![]() , 所以
, 所以![]() 。
。
所以![]() 的值域为{0,1,2,3,4}.
的值域为{0,1,2,3,4}.
|
|
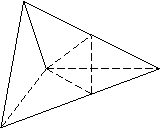
解:(1)取AC中点P,由![]() 知:
知:![]()
![]()
|
|
|
|
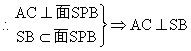
(2)由(1)知:![]() ,又平面
,又平面![]() ,
,![]()
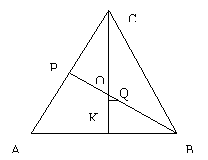 取BP中点Q,连结NQ
取BP中点Q,连结NQ
又N为SB中点
![]() ,而
,而![]() ,
,
![]()
过Q作![]() ,连结NK,
,连结NK,
则![]() 即为二面角N-CM-B的平面角
即为二面角N-CM-B的平面角
设CM交BP于O,则![]() ,
,![]()
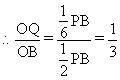
![]()
![]()
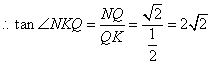
![]()
所以二面角N-CM-B的大小为![]() 。
。
(3)由(2)知:![]()
![]()
![]()
设B到平面CMN的距离为d,则
![]() ,
, ![]()
![]()
![]() 点B到平面CMN的距离为
点B到平面CMN的距离为![]() 。
。
19.(本小题满分16分)
解:(1)由![]() 得:
得:![]()
可见:应有![]()
![]()
因此存在常数![]() 使
使![]() 为等比数列。
为等比数列。
(2)由于![]() 是以
是以![]() 为首项2为公比的等比数列
为首项2为公比的等比数列
![]()
![]()
(3)当![]() 时,
时,![]()
![]() 。
。
而![]()
![]()
![]() (
(![]() )
)
![]()
![]() 当
当![]() 时,
时,![]() 。
。
 20.(本小题满分15分)
20.(本小题满分15分)
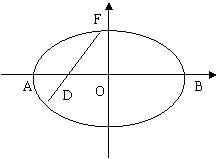
解:(1)如图,建立平面直角坐标系,则D(-1,0)
弦EF所在的直线方程为![]()
设椭圆方程为![]()
设![]() ,由
,由![]() 知:
知:![]()
联立方程组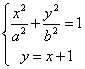 ,消去x得:
,消去x得:![]()
由题意知:![]() ,
,![]()
![]()
由韦达定理知:![]()
![]()
消去![]() 得:
得:![]() ,化简整理得:
,化简整理得:![]()
![]()
![]() 解得:
解得:![]()
![]()
即:椭圆的长轴长的取值范围为![]() 。
。
(2)若D为椭圆的焦点,则c=1,![]()
由(1)知:![]()
![]()
![]()
![]() 椭圆方程为:
椭圆方程为: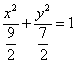 。
。