高考理科数学模拟试题(理科4)
一、选择题:本大题共8小题,每小题5分,共40分。
1.定义运算![]() ,则符合条件
,则符合条件![]() 的复数z为( )
的复数z为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知点P
![]() 在圆C:
在圆C: ![]() 上, 点P关于直线
上, 点P关于直线![]() 的对称点也在圆C上,则实数
的对称点也在圆C上,则实数![]() ,
,![]() 的值为 ( ) .
的值为 ( ) .
A. ![]()
![]()
![]()
![]() B.
B. ![]()
![]()
![]()
![]() C.
C. ![]()
![]()
![]()
![]() D.
D. ![]()
![]()
![]()
![]()
3.设![]()
![]() 使得
使得![]() 是
是![]() 的必要但不充分条件的实数
的必要但不充分条件的实数![]() 的取值范围是 ( )
的取值范围是 ( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.![]()
4.若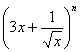 的展开式中各项系数之和为1024,则展开式中含x的整数次幂的项共有( )
的展开式中各项系数之和为1024,则展开式中含x的整数次幂的项共有( )
A.2项 B.3项 C.5项 D.6项
5.设函数![]()
![]()
![]() .若将
.若将![]() 的图象沿x轴向右平移
的图象沿x轴向右平移![]() 个单位长度,得到的图象经过坐标原点;若将
个单位长度,得到的图象经过坐标原点;若将![]() 的图象上所有的点的横坐标缩短到原来的
的图象上所有的点的横坐标缩短到原来的![]() 倍(纵坐标不变), 得到的图象经过点
倍(纵坐标不变), 得到的图象经过点![]() . 则 ( )
. 则 ( )
A.![]() B.
B.![]() C.
C. ![]() D. 适合条件的
D. 适合条件的![]() 不存在
不存在
6.空间四条直线a,b,c,d,满足a⊥b,b⊥c,c⊥d,d⊥a,则必有 ( )
A.a⊥c B.b⊥d C.b∥d 或a∥c D.b∥d 且a∥c
 7.若关于
7.若关于![]() 的不等式
的不等式![]() ≤
≤![]() +4的解集是M,则对任意实数
+4的解集是M,则对任意实数![]() ,总有( )
,总有( )
A. 2∈M,0∈M B. 2![]() M,0
M,0![]() M
M
C. 2∈M,0![]() M D. 2
M D. 2![]() M,0∈M.
M,0∈M.
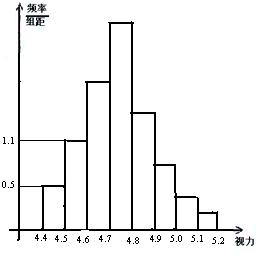
8.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道后5组的频数成等比数列,设视力在4.6到![]() 之间的学生数为
之间的学生数为![]() 最大频率为
最大频率为![]() ,则a, b的值分别为( )
,则a, b的值分别为( )
A.77, 0.53 B.70, 0.32
C.77, 5.3 D.70, 3.2
二、填空题:本大题共6小题,每小题5分,共30分。
必做题:
9.. 如下图1,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的侧面积为__________.
10.如下图2,是计算![]() 的程序框图,判断框应填的内容是___________,处理框应填的内容是____________.
的程序框图,判断框应填的内容是___________,处理框应填的内容是____________.
11. 在坐标平面上,不等式组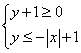 所表示的平面区域的周长为
.
所表示的平面区域的周长为
.
12.已知函数![]() (
(![]() ),其中[x]表示不超过x的最大整数,如[-2.1]=-3,[-3]=-3,[2.5]=2.定义
),其中[x]表示不超过x的最大整数,如[-2.1]=-3,[-3]=-3,[2.5]=2.定义![]() 是函数
是函数![]() 的值域中的元素个数,数列
的值域中的元素个数,数列![]() 的前n项和为
的前n项和为![]() ,则满足
,则满足![]()
![]() 的最大正整数n= .
的最大正整数n= .
选做题:
13. 已知![]() (其中
(其中![]() 且
且![]() 的最大值是7,则
的最大值是7,则![]() .
.
14.将极坐标方程![]() 化为直角坐标方程是______________.
化为直角坐标方程是______________.
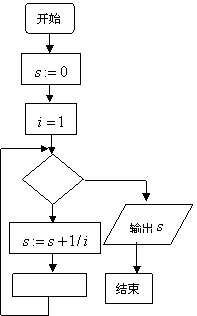
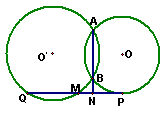 15.如下图3,⊙
15.如下图3,⊙![]() 和⊙O相交于
和⊙O相交于![]() 和
和![]() ,
, ![]() 切⊙O于
切⊙O于![]() ,交⊙
,交⊙![]() 于
于![]()
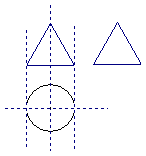 和
和![]() ,交
,交![]() 的延长线于
的延长线于![]() ,
,![]() =
=![]() ,
,![]() =15,则
=15,则 ![]() =__________.
=__________.
三、解答题:本大题共6小题,共80分. 解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)在ΔABC中,![]()
![]()
⑴求AB边的长度;
⑵求 ![]() 的值.
的值.
17.(本小题满分12分)某智力测试有5道试题。假定任何智力正常的人答对每道题的概率都是![]() .
.
⑴求智力正常的人将这5道试题都答错了的概率及至少答对了的4道试题的概率;
⑵如果甲将这5道试题都答错了,乙答对了的4道试题, 答错了1道试题。能否判定甲的智力低于正常水平,乙的智力高于正常水平。请运用所学概率知识表达你的观点。
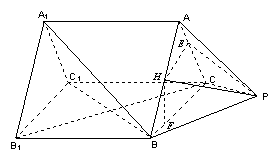
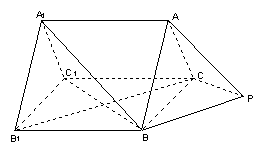 18.(本题满分14分)如图,已知正三棱柱
18.(本题满分14分)如图,已知正三棱柱![]() 中,
中,![]() ,
,![]() ,三棱锥
,三棱锥![]() 中,
中,![]() ,且
,且![]() 。
。
(1)求证:![]() ;
;
(2)求二面角![]() 的大小的正切值;
的大小的正切值;
(3)求点![]() 到平面
到平面![]() 的距离。
的距离。
19.(本题满分14分)已知数列![]() 中,
中,![]() ,
, ![]() .数列
.数列![]() 满足:
满足:![]()
(Ⅰ)求证: ![]() ; (Ⅱ) 求数列
; (Ⅱ) 求数列![]() 的通项公式;
的通项公式;
(Ⅲ) 当n为偶数时,求证:![]() .
.
20. (本题满分14分)设椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,已知椭圆
,已知椭圆![]() 上的任意一点
上的任意一点![]() ,满足
,满足![]() ,过
,过![]() 作垂直于椭圆长轴的弦长为3.
作垂直于椭圆长轴的弦长为3.
(1)求椭圆![]() 的方程;
的方程;
(2)若过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
21.(本题满分14分)已知函数![]() ,
,![]()
![]() .
.
(Ⅰ)当![]() 时,若
时,若![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(Ⅱ)求满足下列条件的所有实数对![]() :当
:当![]() 是整数时,存在
是整数时,存在![]() ,使得
,使得![]() 是
是![]() 的最大值,
的最大值,![]() 是
是![]() 的最小值;
的最小值;
(Ⅲ)对满足(Ⅱ)的条件的一个实数对![]() ,试构造一个定义在
,试构造一个定义在![]() ,且
,且![]() 上的函数
上的函数![]() ,使当
,使当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() 取得最大值的自变量的值构成以
取得最大值的自变量的值构成以![]() 为首项的等差数列.
为首项的等差数列.
数学试题(理科4)参考答案
1~8: C B A B A C A B
9. ![]() ; 10.
; 10. ![]() ,
,![]() ; 11.
; 11. ![]() ; 12. 9; 13. 9; 14.
; 12. 9; 13. 9; 14. ![]() ; 15.
; 15. ![]()
16.解:(1)![]()
![]()
![]()
![]()
∴![]() 即AB边的长度为2.
…………… …………5分
即AB边的长度为2.
…………… …………5分
(2)由已知及(1)有:![]()
![]()
∴![]() ……………8分
……………8分
由正弦定理得: ![]() ……………10分
……………10分
∴![]() =
=![]() …………12分
…………12分
17.解:⑴智力正常的人将这5道试题都答错了的概率
为![]() ……………3分
……………3分
答对了的4道试题的概率为![]()
答对了的5道试题的概率为![]()
∴智力正常的人答对了的4道试题以上的概率为![]() …7分
…7分
⑵智力正常的人将这5道试题都答错了的概率![]() 因而不能判定甲的智力低于正常水平
……9分
因而不能判定甲的智力低于正常水平
……9分
 智力正常的人答对了的4道试题以上的概率
智力正常的人答对了的4道试题以上的概率![]() .根据小概率事件在一次试验中几乎不发生的原理知,假设乙的智力在正常水平, 答对了的4道试题的情况几乎不发生.从而可以认定乙的智力高于正常水平。
…………12分
.根据小概率事件在一次试验中几乎不发生的原理知,假设乙的智力在正常水平, 答对了的4道试题的情况几乎不发生.从而可以认定乙的智力高于正常水平。
…………12分
18.解法一:
(1)在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,取
,取![]() 中点
中点![]() ,
,
![]() ,
, ![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,又
,又![]() 均为锐角,∴
均为锐角,∴![]() , ---------------2分
, ---------------2分
![]() ,又
,又![]() 外,
外, ![]() . ---------------4分
. ---------------4分
(2)∵平面![]()
![]() 平面
平面![]() ,∴
,∴![]() ,过
,过![]() 作
作![]() 于
于![]() ,连结
,连结![]() ,
,
则![]() ,
, ![]() 为二面角
为二面角![]() 的平面角, ------------------------6分
的平面角, ------------------------6分
易知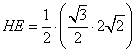 =
=![]() ,∴
,∴![]() , ------------------------9分
, ------------------------9分
(3)![]() ,
,![]() 点到平面
点到平面![]() 的距离,就是
的距离,就是![]() 到平面
到平面![]() 的距离, --------11分
的距离, --------11分
过![]() 作
作![]() 于
于![]() ,则
,则![]() ,
,![]() 的长度即为所求, 由上
的长度即为所求, 由上![]() (或用等体积
(或用等体积![]() 求)----------------------------------14分
求)----------------------------------14分
解法二:建立图示空间直角坐标系.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)![]()
(2)利用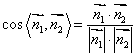 ,其中
,其中![]() 分别为两个半平面的法向量..
分别为两个半平面的法向量..
(3)利用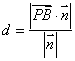 ,其中
,其中![]() 为平面
为平面![]() 的法向量。
的法向量。
19. (Ⅰ)证明: 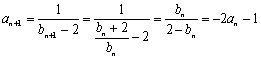
![]() ………... 3分
………... 3分
(Ⅱ)![]()
![]() ∴
∴ ![]() ……………………….………..5分
……………………….………..5分
又 ![]() ∴
∴ ![]() 为等比数列………………………………………….6分
为等比数列………………………………………….6分
∴ ![]() ∴
∴ ![]() ……………………………………………………8分
……………………………………………………8分
(Ⅲ)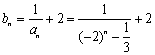 ∴
∴ 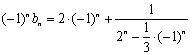 …………………. 10分
…………………. 10分
当n为偶数时,![]()
![]()
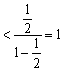 …14分
…14分
20. 解:(1)设点![]()
![]() ,则
,则![]() ,
,
![]() ,
,![]()
![]() ,又
,又![]() ,
,
![]() ,∴椭圆的方程为:
,∴椭圆的方程为:![]()
(2)当过![]() 直线
直线![]() 的斜率不存在时,点
的斜率不存在时,点![]() ,则
,则![]() ;
;
当过![]() 直线
直线![]() 的斜率存在时,设斜率为
的斜率存在时,设斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
设![]() , 由
, 由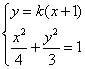 得:
得:![]()
![]()
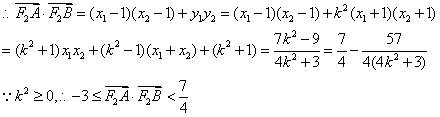
综合以上情形,得:![]()
21. 解:(Ⅰ)当![]() 时,
时,![]() ,
,
若![]() ,
,![]() ,则
,则![]() 在
在![]() 上单调递减,不符题意.
上单调递减,不符题意.
故![]() ,要使
,要使![]() 在
在![]() 上单调递增,必须满足
上单调递增,必须满足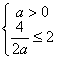 ,∴
,∴![]() .
.
(Ⅱ)若![]() ,
,![]() ,则
,则![]() 无最大值,故
无最大值,故![]() ,∴
,∴![]() 为二次函数.
为二次函数.
要使![]() 有最大值,必须满足
有最大值,必须满足![]() 即
即![]() ,且
,且![]() .
.
此时,![]() 时,
时,![]() 有最大值.
有最大值.
又![]() 取最小值时,
取最小值时,![]() ,依题意,有
,依题意,有![]() ,
,
则![]() .
.
∵![]() ,且
,且![]() ,∴
,∴![]() ,得
,得![]() ,此时
,此时![]() 或
或![]() .
.
∴满足条件的实数对![]() 是
是![]() .
.
(Ⅲ)当实数对![]() 是
是![]() 时,
时,![]() .
.
依题意,只需构造以2(或2的正整数倍)为周期的周期函数即可.
如对![]() ,
,![]() ,
,
此时,![]() ,
,
故![]() .
.