高考预测理科数学试卷
注意事项:
1.本试题分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.
2.请将第I卷选择题的答案用2B铅笔填涂在答题卡上,第II卷在各题后直接作答。
参考公式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B) S=4πR2
如果事件A、B相互独立, 其中R表示球的半径
那么P(A·B)=P(A)·P(B) 球的体积公式
如果事件A在一次试验中发生的概率 ![]()
是P,那么n次独立重复试验中恰好发 其中R表示球的半径
生k 次的概率Pn(k)=![]()
第Ⅰ卷
一、选择题(本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是最符合题目要求的。)
1.设![]() 满足C
满足C![]()
![]() 的集合C的个数为
的集合C的个数为
(A)0 (B)1 (C)2 (D)4
2. 已知函数![]() 有反函数
有反函数![]() ,且函数
,且函数![]() 的图象过点(1,3),则函数
的图象过点(1,3),则函数![]() 的图象必过点
的图象必过点
(A)(1,3) (B)(3,1) (C) ![]() (D)(1,1)
(D)(1,1)
3.若复数![]() 是纯虚数,则实数
是纯虚数,则实数![]() 的值为
的值为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
4.已知条件![]() ,条件
,条件![]() ,若
,若![]() 和
和![]() 中有且只有一个成立,则
中有且只有一个成立,则![]() 的取值范围是
的取值范围是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.下列命题不正确的是(其中l,m表示直线,α,β, r表示平面) ( )
A.若l⊥m,l⊥α,m⊥β,则α⊥β B.若l⊥m,l![]() α,m
α,m![]() β,则α⊥β
β,则α⊥β
C.若α⊥r,β//r,则α⊥β D.若l//m,l⊥α,m![]() β,则α⊥β
β,则α⊥β
6.6人排成一排,要求甲、乙两人中间恰好有1人,且甲,乙都不与丙相邻,则不同的排列
方法有 ( )
A.24 B.72 C.48 D.36
7.已知F1,F2是双曲线![]() 的左右焦点,过F1作垂直于x轴的直线
的左右焦点,过F1作垂直于x轴的直线
交双曲线于A、B两点,若△ABF2为锐角三角形,则双曲线离心率的取值范围是( )
A.(1,1+![]() ) B.(1+
) B.(1+![]() ,+∞) C.(1-
,+∞) C.(1-![]() ,1+
,1+![]() )D.(
)D.(![]() ,
,![]() +1)
+1)
| |
A.-2 B.-![]() C.
C.![]() D.2
D.2
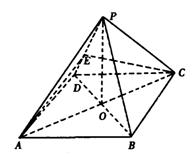
9.正四面体的内切球,与各棱都相切的球,外接球的半径之比为 ( )
A.1:![]() :
:![]() B.1:
B.1:![]() :3 C.1:
:3 C.1:![]() :2 D.1:2:3
:2 D.1:2:3
10.函数f(x)=x2-2ax+a在区间(-∞,1)上有最小值,则函数![]() 在区间(1,
在区间(1,
+∞)上一定 ( )
A.有最小值 B.有最大值 C.是减函数 D.是增函数
第Ⅱ卷
二、填空题(本大题共6小题,每小题4分,共24分,把答案填在题中的横线上)
11.在由正数组成的等比数列{an}中,a1+a2=1,a3+a4=4,则a4+a5=_________
12.设f(x)=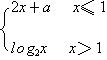 ,若
,若![]() f (x)存在,则常数a=___________
f (x)存在,则常数a=___________
13.已知![]() 的展开式中x2的系数与
的展开式中x2的系数与![]() 的展开式中x3的二项式系数相等,则cosθ= .
的展开式中x3的二项式系数相等,则cosθ= .
|
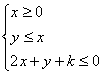 (k为常数)时,能使Z=x+3y的最大值为12的k的值是 .
(k为常数)时,能使Z=x+3y的最大值为12的k的值是 .
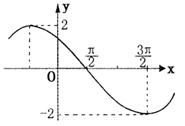
15.已知![]()
其导函数f′(x)的图象(部分)如图,则f(x)的解析式
为 .
16.已知定义在R上的函数f(x)的图象关于点(-![]() ,0)成为中心对称图形,且满足
,0)成为中心对称图形,且满足
![]() 的值为 .
的值为 .
三、解答题(本大题共6个小题,共76分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分13分)
(本题满分12分)已知锐角△ABC三个内角为A、B、C,向量![]() 与向量
与向量![]() 是共线向量.
是共线向量.
①求角A.②求函数![]() 的最大值.
的最大值.
18.(本小题满分13分)一个口袋里面装有2个白球4个黑球,这些球除颜色差别外没有其它的区别. 现在从袋中随机取出一个来记好颜色,然后放回并搅匀,之后再随机取球记色,再放回搅匀,…. 记数列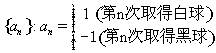 ,数列
,数列![]() 的前n项和记为
的前n项和记为![]() ①.求事件“
①.求事件“![]() =2”的概率; ②求
=2”的概率; ②求![]() 取值的分布列和数学期望
取值的分布列和数学期望![]() .
.
19.(本小题满分13分)如图,正方形ABCD中,![]() ,点E在PD上,PE:ED=2:1。
,点E在PD上,PE:ED=2:1。
|
(2)求二面角A—PD—C的余弦值;
(3)求点B到平面PDC的距离。
20.(本小题满分13分)
已知函数![]()
(1)求数列{an}的通项an;
(2)若数列{bn}的前n项和![]() 求Tn.
求Tn.
21.(本小题满分12分)
设函数y=f(x)=x(x-a)(x-b) (a,b∈R)
(1)a≠b,ab≠0,过两点(0,0),(a,0)的中点作与x轴垂直的直线与函数y=f(x)的图象交于点P(x0,f(x0)),求证:函数y=f(x)在点P处的切线经过点(b,0);
(2)若a=b(a≠0)且当x∈[0,a+1]时,f(x)<2a2恒成立,求实数a的取值范围 。
22.(本小题满分12分)
|
(1)求椭圆的方程;
(2)若AB上的一点F满足![]()
求证:CF平分∠BCA;
(3)对于椭圆上的两点P、Q,∠PCQ的平分线总是垂直于x轴时,是否存在实数λ,使得![]()
参考答案
一、选择题:
1—5BCAAB 6—10BABBD 11—12AC
二、填空题:
11.8 12.-2 13.![]() 14.-9 15.
14.-9 15.![]() 16.1
16.1
三、解答题:
17.解:(1)![]() 共线
共线![]() …….2’
…….2’
![]() ……………2’ 而
……………2’ 而![]() 为锐角,所以
为锐角,所以![]()
![]() …...2’
…...2’
(2)![]()
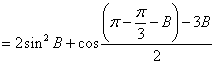
![]()
![]()
![]()
![]() …………..3’
…………..3’
![]()
![]() 时,
时,![]() ………….4’
………….4’
18.解:(1)事件![]() 只能是“四次取球中出现三次白球一次黑球”,
只能是“四次取球中出现三次白球一次黑球”,
每次取得白球的概率为![]() ;取得黑球的概率是
;取得黑球的概率是![]() …………..2’
…………..2’
于是![]() ………………………………..2’
………………………………..2’
(2)![]() 可能的取值有
可能的取值有![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,…………………5’
,…………………5’
|
|
|
| 0 | 2 | 4 |
|
|
|
|
|
|
|
于是![]() 取值的分布列为
取值的分布列为
………………………………………….2’
![]() …………2’
…………2’
19.(1)![]()
(2)∠CEA为二面角A—PD—C的平面角,![]()
(3)点B到平面PDC的距离为![]()
20.解:(1)![]()
![]() 是首项a1,公差d=3的等差数列
是首项a1,公差d=3的等差数列 ![]()
(2)![]()
![]()
2Tn=1·2+4·22+7·22+…+(3n-2)·2n
两式相减-Tn=1+3(2+22+…+2n-1)-(3n-2)·2n
=-5-(3n-5)·2n
∴Tn=(3n-5)·2n+5
21.解:(1)![]()
所求切线斜率为 ![]()
切线 ![]()
令y=0 得x=b ∴函数y=f(x)过点P的切线过点(b,0)
(2)![]()
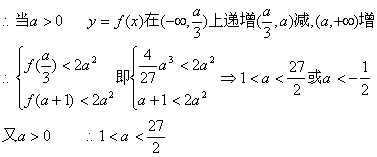
当a<0时,函数y=f(x)在(![]() ,+∞)上递增
,+∞)上递增
∴f(1-a)<2a2·即(1-a)(1-a-a)2<2a2![]() 4a3-6a2+5a-1>0
4a3-6a2+5a-1>0
令g(a)=4a3-ba2+5a-1
g′(a)=12a2-12a+5=12(a-![]() )2+2>0
)2+2>0
∴g(a)在(-∞,0)单增 又g(0)=-1<0 ∴g(a)>0无解
综上 1<a<![]()
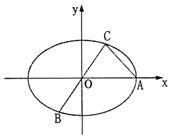
22.(I)解:![]()
又![]()
∴△AOC是等腰直角三角形
∵A(2,0),∴C(1,1)而点C在椭圆上,
∴![]()
∴所求椭圆方程为![]()
(Ⅱ)证明C(1,1),则B(-1,-1)
又![]()
即点F分![]() 所成的定比为2.
所成的定比为2.
设![]()
![]()
CF⊥x轴,
∴∠ACF=∠FCB=45°,即CF平分∠BCA.
(Ⅲ)对于椭圆上两点P、Q,∵∠PCQ的平分线总是垂直于x轴
∴PC与CQ所在直线关于x=1对称,kpC=k,则kcQ=-k,
设C(1,1),则PC的直线方程y-1=k(x-1)![]() y=k(x-1)+1 ①
y=k(x-1)+1 ①
QC的直线方y-1=-k(x-1) ![]() y=-k(x-1)+1 ②
y=-k(x-1)+1 ②
将①代入![]() 得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0
③
得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0
③
∵C(1,1)在椭圆上,∴x=1是方程③的一个根,
∴xp·1=![]() =1同理将②代入x2+3y2=4得
=1同理将②代入x2+3y2=4得
(1+3k2)x2-6k(k+1)x+3k2+6k-1=0 ④
∵C(1,1)在椭圆上,
∴x=1是方程④的一个根,
∴xQ·1= ![]()
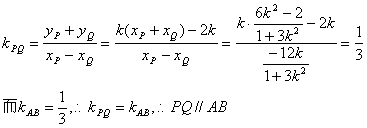
∴存在实数λ,使得![]() .
.